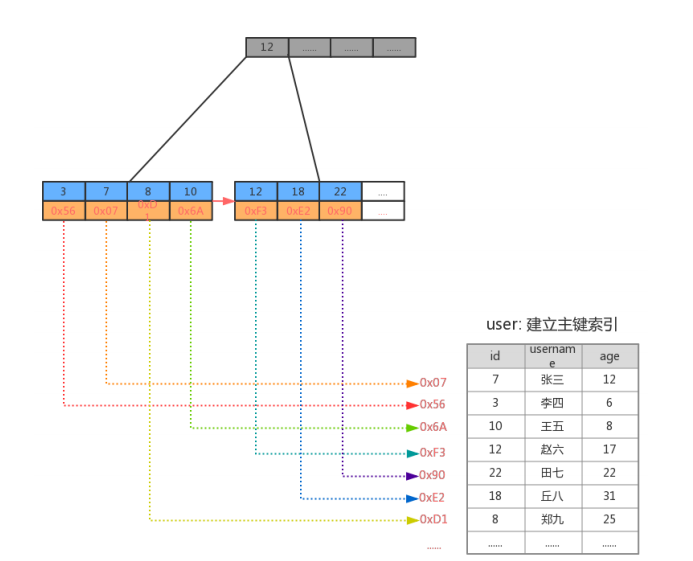
什么是前缀和

如果一个数组a的元素为$a_1,a_2,a_3,a_4,a_5...a_i$.
而另一个数组b为$a_1,a_1+a_2,a_1+a_2+a_3....,a_1+..+a_i$
那么数组b就是a的前缀和了。

用途

那么前缀和有些什么用呢。
我们让$b_1,b_2...b_i$代表b的元素
那么我们可以轻易的用一次减法得到某个区间的和如$a_5+a_6+...+a_{100}$等于$b_{100}-b_5$得到这个差值，而不用每次都一个个加。

什么时候用

1. 经常需要求区间和
2. 而在一些题目中，数组a在题意中是变化的，而其前缀和不变，那么很有可能就是使用前缀和

例题

[蓝桥杯 2021 国 ABC] 123

题目描述

小蓝发现了一个有趣的数列, 这个数列的前几项如下:

$1,1,2,1,2,3,1,2,3,4,\dots$

小蓝发现, 这个数列前 $1$ 项是整数 $1$ , 接下来 $2$ 项是整数 $1$ 至 $2$ , 接下来 $3$ 项是整数 $1$ 至 $3$ , 接下来 $4$ 项是整数 $1$ 至 $4$ , 依次类推。

小蓝想知道, 这个数列中, 连续一段的和是多少。

输入格式

输入的第一行包含一个整数 $T$, 表示询问的个数。

接下来 $T$ 行, 每行包含一组询问, 其中第 $i$ 行包含两个整数 $l_i$ 和 $r_i$, 表示 询问数列中第 $l_i$ 个数到第 $r_i$ 个数的和。

输出格式

输出 $T$ 行, 每行包含一个整数表示对应询问的答案。

样例 #1

样例输入 #1

3
1 1
1 3
5 8

样例输出 #1

1
4
8

提示

对于 $10\%$ 的评测用例, $1\le T\le 30,1\le l_i\le r_i\le 100$ 。
对于 $20\%$ 的评测用例, $1\le T\le 100,1\le l_i\le r_i\le 1000$ 。
对于 $40\%$ 的评测用例, $1\le T\le 1000,1\le l_i\le r_i\le 10^6$ 。
对于 $70\%$ 的评测用例, $1\le T\le 10000,1\le l_i\le r_i\le 10^9$ 。
对于 $80\%$ 的评测用例, $1\le T\le 1000,1\le l_i\le r_i\le 10^{12}$ 。
对于 $90\%$ 的评测用例, $1\le T\le 10000,1\le l_i\le r_i\le 10^{12}$ 。
对于所有评测用例, $1\le T\le 100000,1\le l_i\le r_i\le 10^{12}$ 。
蓝桥杯 2021 国赛 A 组 E 题（B 组 F 题，C 组 F 题）。

思路

根据题目可以知道是得到某个范围的和。那么我们就可以考虑到前缀和。
我们看项，（num）项的和值是$1,1+2,1+2+3,1+2+3+\mathrm{4....}$
每一项的项数为$1，2，3，\mathrm{4...}$个数。

但是我们需要的是从开头的项，那么用前缀和得到这样的表示数量的数组$1,3,6,\mathrm{10....}$。而我们发现这个数组其实和num数组一样的。我们需要求某个范围的和，那么我们构造一个前缀和(sum数组)$1，4，10，\mathrm{16...}$如果想要求6到10项和就算sum[4]-sum[3]就可以了。如果想要5到8呢。
我们也可以先得到sum[4]-sum[3]然后减去9,10代表的加上5，6就是答案了。

那么我们只剩下一个问题了，如何得到4和3还有减去的数和加上的数。
我们发现这个围绕的都是6和10项。10是num[4]代表的，6是num[3]代表的。
加和减是和6，10的差距。

如何得到呢。我们可以发现num是顺序的，就可以用二分，得到其小于等于这个值的位置。（java直接Arrays.binarySearch插入点就可以了）

emm好像还差了，9、10、5、6代表的数如何求。我们可以知道，对于10的数一定是4，因为每一项都是从1到i来的，所以最后一个一定是i。第一个是1.
那么我们可以用一个求和公式来计算，$(首项+末项)\ast 项数/2$
项数num[i] - 当前项。末项为i,首项为i-项数。

下面来根据代码食用。

代码

import java.io.*;
import java.util.Arrays;

public class Main {
    static final PrintWriter print = new PrintWriter(System.out);
    // 更快的输入输出
    static final StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static int nextInt() throws IOException {
        st.nextToken();
        return (int) st.nval;
    }

    public static long nextLong() throws IOException {
        st.nextToken();
        return (long) st.nval;
    }

    public static void main(String[] args) throws IOException {
        int m = 2000000;
        
        long[] num = new long[m];
        //构造前缀和num
        for (int i = 1; i < m; i++) {
            num[i] = num[i - 1] + i;
        }
        
        //构造前缀和sum
        long[] sum = Arrays.copyOf(num, m);
        Arrays.parallelPrefix(sum, Long::sum);
        
        //注释掉的是因为最大数据在10的12次方，测试m是否能够到达最大
//        System.out.println(num[m-1]);
//        System.out.println(sum[m-1]);
        int n = nextInt();
        for (int i = 0; i < n; i++) {
            long a = nextLong();
            long b = nextLong();

            //寻找下标。
            int x = Arrays.binarySearch(num, a);
            int y = Arrays.binarySearch(num, b);
            x = x > 0 ? x : -x - 1;
            y = y > 0 ? y : -y - 1;

			//获取区间和
            long ans = sum[y] - sum[x];

			//获取项数
            long z = num[y] - b;
            //求和
            ans -= (2 * y - z + 1) * z / 2;
            z = num[x] - a + 1;
            ans += (2 * x - z + 1) * z / 2;
            //获得答案
            print.println(ans);
        }
        print.flush();

    }
}

灵能传输(蓝桥杯96%，洛谷ac)

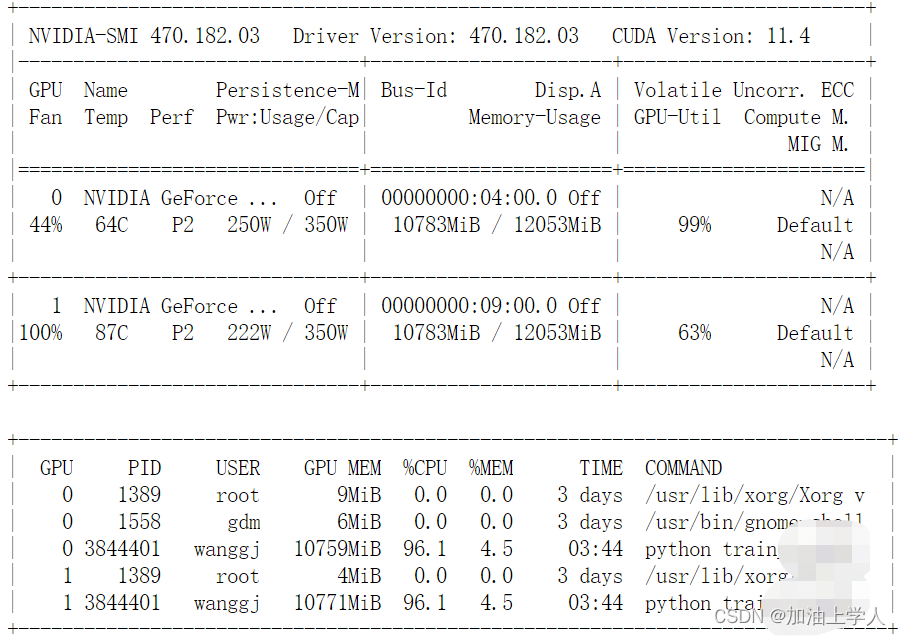
我只做到96%，不能ac，最后一个超时了。但是在洛谷没有超时

[蓝桥杯 2019 省 B] 灵能传输

题目背景

在游戏《星际争霸 II》中，高阶圣堂武士作为星灵的重要 AOE 单位，在游戏的中后期发挥着重要的作用，其技能“灵能风暴”可以消耗大量的灵能对一片区域内的敌军造成毁灭性的伤害。经常用于对抗人类的生化部队和虫族的刺蛇飞龙等低血量单位

题目描述

你控制着 $n$ 名高阶圣堂武士，方便起见标为 $1,2,\cdots ,n$。每名高阶圣堂武士需要一定的灵能来战斗，每个人有一个灵能值 $a_i$ 表示其拥有的灵能的多少（$a_i$ 非负表示这名高阶圣堂武士比在最佳状态下多余了 $a_i$ 点灵能，$a_i$ 为负则表示这名高阶圣堂武士还需要 $-a_i$ 点灵能才能到达最佳战斗状态）。现在系统赋予了你的高阶圣堂武士一个能力，传递灵能，每次你可以选择一个 $i\in [2,n-1]$，若 $a_i\ge 0$ 则其两旁的高阶圣堂武士，也就是 $i-1$ 、 $i+1$ 这两名高阶圣堂武士会从 $i$ 这名高阶圣堂武士这里各抽取 $a_i$ 点灵能；若 $a_i<0$ 则其两旁的高阶圣堂武士，也就是 $i-1,i+1$ 这两名高阶圣堂武士会给 $i$ 这名高阶圣堂武士 $-a_i$ 点灵能。形式化来讲就是 $(a_{i-1},a_i,a_{i+1})\leftarrow (a_{i-1}+a_i,-a_i,a_{i+1}+a_i)$。

灵能是非常高效的作战工具，同时也非常危险且不稳定，一位高阶圣堂武士拥有的灵能过多或者过少都不好，定义一组高阶圣堂武士的不稳定度为 max ⁡ i = 1 n { ∣ a i ∣ } \max\limits_{i=1}^n\{|a_i|\} i=1maxn​{∣ai​∣}，请你通过不限次数的传递灵能操作使得你控制的这一组高阶圣堂武士的不稳定度最小。

输入格式

本题包含多组询问。输入的第一行包含一个正整数 $T$ 表示询问组数。

接下来依次输入每一组询问。

每组询问的第一行包含一个正整数 $n$，表示高阶圣堂武士的数量。

接下来一行包含 $n$ 个数 $a_1,a_2,\cdots ,a_n$。

输出格式

输出 $T$ 行。每行一个整数依次表示每组询问的答案。

样例 #1

样例输入 #1

3 3
5 -2 3
4
0 0 0 0
3
1 2 3

样例输出 #1

3 0 3

样例 #2

样例输入 #2

3 4
-1 -2 -3 7
4
2 3 4 -8
5
-1 -1 6 -1 -1

样例输出 #2

5 7 4

样例 #3

样例输入 #3

见文件trans3.in。

样例输出 #3

见文件trans3.ans。

提示

【样例说明】

对于第一组询问：

对 $2$ 号高阶圣堂武士进行传输操作后 $a_1=3$，$a_2=2$，$a_3=1$。答案为 $3$。

对于第二组询问：

这一组高阶圣堂武士拥有的灵能都正好可以让他们达到最佳战斗状态。

【数据规模与约定】

对于所有评测用例，$T\le 3$，$3\le n\le 3\times 10^5$，$|a_i|\le 10^9$。

蓝桥杯 2019 年省赛 B 组 J 题。

思路

我们看到这句话$(a_{i-1},a_i,a_{i+1})\leftarrow (a_{i-1}+a_i,-a_i,a_{i+1}+a_i)$。
其前缀和$(a_{i-1},a_{i-1}+a_i,a_{i-1}+a_i+a_{i+1})\leftarrow (a_{i-1}+a_i,a_{i-1}+a_i+a_{i+1})$
后面前缀和就用s表示了就是$s_{i-1},s_i,si+1\leftarrow s_i,si-1,si+1$
我们可以发现，每次操作前缀和都只是换了个变罢了。

而我们题目的意思就是让2项的差值的最大值要最小。也就是$max|s_n-s_{n-1}|$最小
那么如何可以到最小呢。

猜测是顺序最小，我们来具体看看。看图，这个应该还是很明显的

我们对其顺序排序就可以了。但是也没有就此就结束了。最后一个是不能进行交换的，

还有个问题就是有负数。所以我们需要一个s0=0来衡量一下。
排序之后。

s0到min->sn->max->sn我们怎么来选择呢，这部分是有重复的。
我们是怎么来选呢，是隔一个选还是2个
我们来看1个的

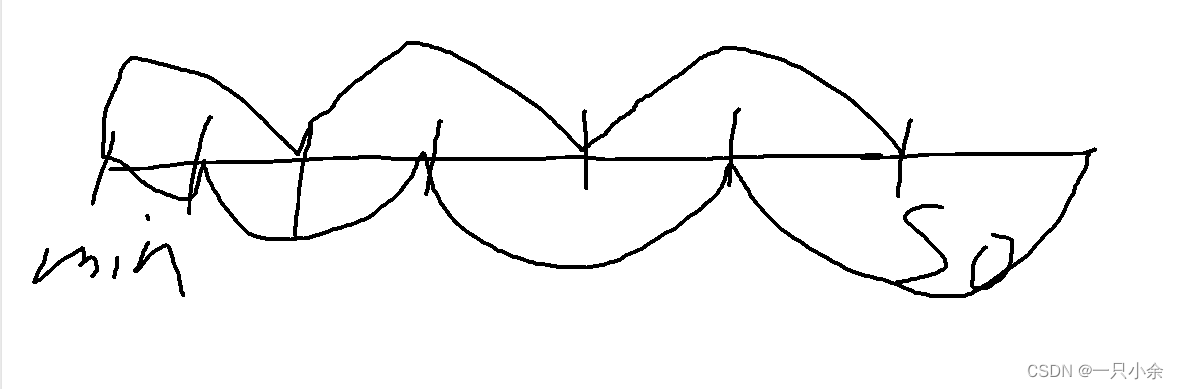
2个的

2个的这个最大跨度肯定会比1个的要大呀，所以我们隔着一个选一个。

代码

import java.io.*;
import java.util.Arrays;

public class Main {
    static final PrintWriter print = new PrintWriter(System.out);
    static final StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    public static int nextInt() throws IOException {
        st.nextToken();
        return (int) st.nval;
    }

    public static long nextLong() throws IOException {
        st.nextToken();
        return (long) st.nval;
    }


    public static void main(String[] args) throws IOException {
        int t = nextInt();
        for (int k = 0; k < t; k++) {
            int n = nextInt();
            long[] a = new long[n + 1];
            // 构造前缀和
            for (int i = 1; i <= n; i++) {
                a[i] = nextInt() + a[i - 1];
            }
//            for (int i = 1; i <= n; i++) {
//                a[i] = nextInt();
//            }
//            Arrays.parallelPrefix(a, Long::sum);
			
            long n0 = Math.min(a[0], a[n]);
            long nn = Math.max(a[0], a[n]);
            //排序
            Arrays.sort(a);
            //找到s0和sn
            int s0 = 0,sn = 0;
            for (int i = 0; i < n + 1; i++) {
                if (a[i] == n0) {
                    s0 = i;
                    break;
                }
            }
            for (int i = n; i >= 0; i--) {
                if (a[i] == nn) {
                    sn = i;
                    break;
                }
            }
            //找最大值，我们选用标记的方法来解决重复的问题
            long ans = 0;
            long[] b = new long[n + 1];
            boolean[] f = new boolean[n + 1];
            int l = 0, r = n;
            for (int i = s0; i >= 0; i -= 2) {
                b[l++] = a[i];
                f[i] = true;
            }
            for (int i = sn; i <= n; i += 2) {
                b[r--] = a[i];
                f[i] = true;
            }
            for (int i = 0; i <= n; i++) {
                if (!f[i])
                    b[l++] = a[i];
            }
            for (int i = 1; i <= n; i++) {
                ans = Math.max(ans,Math.abs(b[i]-b[i-1]));
            }
            print.println(ans);
        }
        print.flush();
    }
}