前言

NeRF从2020年发展至今，仅仅三年时间，而Follow的工作已呈井喷之势，相信在不久的将来，NeRF会一举重塑三维重建这个业界，甚至重建我们的四维世界（开头先吹一波）。NeRF的发展时间虽短，有几篇工作却在研究领域开始呈现万精油趋势：

• PixelNeRF----泛化法宝
• MipNeRF----近远景重建
• NeRF in the wild----光线变换下的背景重建
• NeuS----用NeRF重建Surface
• Instant-NGP----多尺度Hash编码实现高效渲染

本篇是NeRF必读系列的最后一篇：NeRF in the Wild. 该篇主打一个Appearance Embedding, 由于该方法在生活场景中的普适性被大范围的使用，可以说再以后NeRF的文章中，NeRF-W将成为一篇难以避开的引用文章。

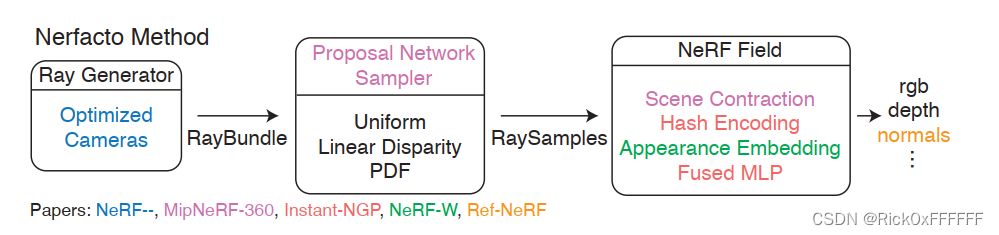
先插一句题外话，现在各行各业都流行一个通用的Framework, 例如搞detection的都有MMCV，MMDETECTION。基于Framework可以快速迭代自己的idea，在知识迅速爆炸的今天，学会各行各业的框架可谓是至关重要！所以在结束本期的paper解析之后，我将开启NeRFStudio系列的解析文章，开始NeRF领域的迅速迭代之旅！在此奉上NeRFStudio的pipeline，可以发现大部分文章我们都已经在前文中学习，仅剩下NeRF-W以及NeRF减减没有解析。下面补齐这两篇。

NeRF-W Main Contributions

1. Appearance Variations Embedding: 户外场景下被重建物体的曝光度，光线，季节、天气等的变换都会影响物体给出的appearance, 作者构造了一个Embedding层用来表征$\nabla V_{apprearance}$的低维描述
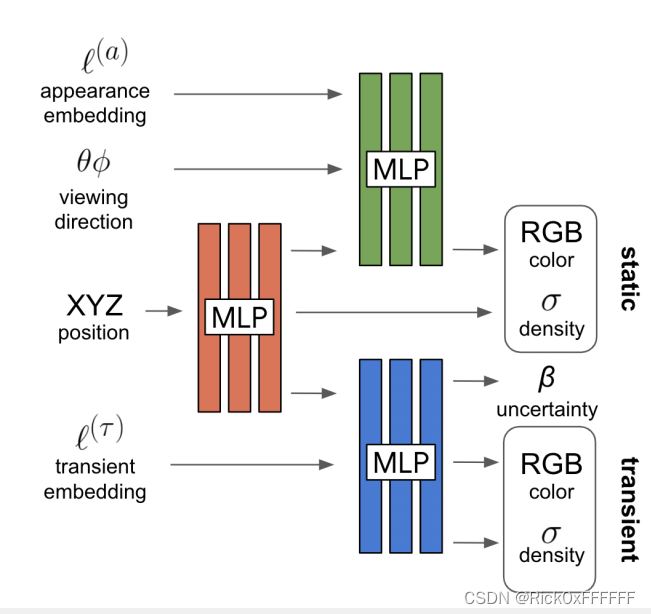
2. Transient Embedding：作者利用将一张图像分解为场景共享部分（shared elements）和依赖于图像的瞬息部分（transient elements，如名胜古迹照的游客）,并利用一个Transient Embedding层无监督地将这两个部分分解开来。具体的pipeline 如下：
   

经典Volumetric Rendering：

$$\begin{gathered} \hat{\mathbf{C}}(\mathbf{r})=\mathcal{R}(\mathbf{r},\mathbf{c},\sigma )=\sum _{k=1}^{K}T(t_k)\alpha (\sigma (t_k){\delta }_k)\mathbf{c}(t_k) \\ \text{where}T(t_k)=exp(-\sum _{k^{\prime }=1}^{k-1}\sigma (t_{k^{\prime }}{\delta }_{k^{\prime }})), \end{gathered}$$
写成MLP的表达式如下：

$$\begin{array}{r}[\sigma (t),\mathbf{z}(\mathbf{t})]=\mathbf{ML}{\mathbf{P}}_{{\theta }_1}({\gamma }_{\mathbf{x}}(\mathbf{r}(\mathbf{t})))\\ \mathbf{c}(\mathbf{t})=\mathbf{ML}{\mathbf{P}}_{{\theta }_2}({\mathbf{z}}_{\mathbf{t}},{\gamma }_{\mathbf{d}}(\mathbf{d}))\end{array}$$

作者为了强调$\sigma (t)$与观测角度无关，额外输出了隐变量$\mathbf{z}(t)$，做为根据$(\mathbf{x},\mathbf{d})$生成color的condition。
最后是Coarse And Fine Loss:
$$\sum _{ij}\Vert \mathbf{C}({\mathbf{r}}_{\mathbf{ij}})-{\hat{\mathbf{C}}}^{\mathbf{c}}({\mathbf{r}}_{\mathbf{ij}}){\Vert }_2^2+\Vert \mathbf{C}({\mathbf{r}}_{\mathbf{ij}})-{\hat{\mathbf{C}}}^{\mathbf{f}}({\mathbf{r}}_{\mathbf{ij}}){\Vert }_2^2$$
以上便是经典的NeRF操作，下面作者开始介绍作者的魔改：

Latent Appearance Modeling

这一段在论文中4.1节，非常简约，作者给每张image分配了一个关联的隐编码$l_i^{(a)}$,$l_i^{(a)}$会随着训练被优化，优化后的公式如下：
$$\begin{gathered} {\hat{\mathbf{C}}}_i(\mathbf{r})=\mathcal{R}(\mathbf{r},\mathbf{c},\sigma ) \\ {\mathbf{c}}_{\mathbf{i}}(\mathbf{t})=\mathbf{ML}{\mathbf{P}}_{{\theta }_2}({\mathbf{z}}_{\mathbf{t}},{\gamma }_{\mathbf{d}}(\mathbf{d}),l_{\mathbf{i}}^{(\mathbf{a})}) \end{gathered}$$
关于$l_i^{(a)}$的故事我会在后面详细述说，感兴趣的读者可以三连，点赞破10我加班更新，扑哧~

Transient Objects

瞬息物体对我们需要渲染的主体部分进行了遮挡，因此最后渲染图片的颜色也应该是不同的，作者按照这个思路增加了一个MLP， 并给出了改进后的渲染公式：
$$\begin{gathered} \hat{\mathbf{C}}(\mathbf{r})=\sum _{k=1}^{K}T(t_k)(\alpha (\sigma (t_k){\delta }_k)\mathbf{c}(t_k)+\alpha ({\sigma }_i^{(\tau )}(t_k){\delta }_k){\mathbf{c}}_i^{(\tau )}(t_k)) \\ \text{where}{T}_i(t_k)=exp(-\sum _{k^{\prime }=1}^{k-1}(\sigma (t_{k^{\prime }})+{\sigma }_i^{(\tau )}(t_{k^{\prime }})){\delta }_{k^{\prime }}) \end{gathered}$$
至此便能刻画出在存在Transient Objects的情况下，Volumetric Rendering的过程了，但作者并没有到此为止，更进一步的优化了Loss的分配比重。对于始终都是静态的图像区域，color的分布方差肯定较小，而transient objects较多的区域，color分布的方差会比较大，对于梯度的方向当然要多给跟方差变化较小的区域~
根据此思路，作者选择在渲染过程中直接估计方差$${\hat{\beta }}_i(\mathbf{r})=\mathcal{R}(\mathbf{r},{\beta }_i,{\sigma }_i^{\tau })$$

经过上述讨论，构建${\text{MLP}}_{{\theta }_3}$如下所示：
$$\begin{gathered} [{\sigma }_i^{(\tau )}(t),{\mathbf{c}}_i^{(\tau )}(t),{\tilde{\beta }}_i(t)]={\text{MLP}}_{{\theta }_3}(\mathbf{z}(t),l_i^{(\tau )}) \\ {\beta }_i(t)={\beta }_{min}+log(1+exp({\tilde{\beta }}_i(t))) \end{gathered}$$
其中下式的意义是将输出从$(-\infty ,+\infty )$映射到$(0,+\infty )$，作者把上述loss构造给了fine model,而coarse model还是使用了经典loss
$$\begin{gathered} L_i(\mathbf{r})=\frac{\Vert {\mathbf{C}}_i(\mathbf{r})-{\hat{\mathbf{C}}}_i(\mathbf{r}){\Vert }_2^2}{2{\beta }_i(\mathbf{r}{)}^2}+\frac{log{\beta }_i(\mathbf{r}{)}^2}{2}+\frac{{\lambda }_{\mu }}{K}\sum _{k=1}^K{\sigma }_i^{(\tau )}(t_k) \\ {L}_{total}=\sum _{ij}{L}_i({\mathbf{r}}_{ij})+\frac{1}{2}\Vert C({\mathbf{r}}_{ij})-{\hat{C}}_i^c({\mathbf{r}}_{ij})\Vert \end{gathered}$$

参考文献

Martin-Brualla, Ricardo, et al. “Nerf in the wild: Neural radiance fields for unconstrained photo collections.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2021.