模拟控制器的离散化
数字PID控制器
Smith预估控制
文章目录
- 模拟控制器的离散化
- 数值积分法
- 一阶后向差分法
- 一阶前向差分法
- 双线性变换法(Tustin)
- 零极点匹配法
- 其他方法
- 数字PID控制器
- 模拟PID控制器的离散化
- 数字PID的改进
- PID控制各环节的作用
- PID参数的整定
- 扩充临界比例度法
- 扩充阶跃响应曲线法
- PID控制器的无扰切换
- Smith预估控制
- 设计纯滞后补偿控制系统
- Smith预估器的编排结构
所谓模拟设计法,即是先按照连续系统的设计方法,使用如频率特性、根轨迹等工具,设计出模拟控制器,再进行离散化,得到数字控制器。
优点是使用我们已经比较熟悉的连续系统的设计方法。缺点是性能比模拟系统差,而且未能完全发挥计算机控制的作用。
模拟设计法的步骤:
- 根据性能指标,设计连续域的传递函数 D ( s ) D(s) D(s)
- 选择合适的离散化方法,将 D ( s ) D(s) D(s)离散化,得到 D ( z ) D(z) D(z)
- 检验计算机控制系统的闭环性能,若不满足,需要改进。如重选离散化方法、提高采样频率、重新设计 D ( s ) D(s) D(s)等
- 将 D ( z ) D(z) D(z)变为数字算法,在计算机上编程实现
模拟控制器的离散化
数值积分法
一阶后向差分法
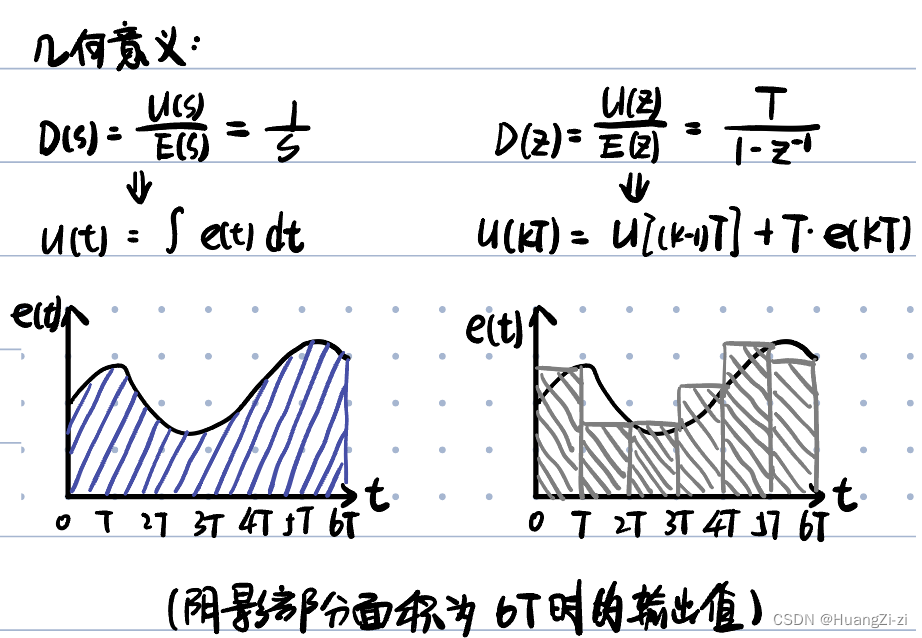
即把微分 d u ( t ) d t \frac{\text{d}u(t)}{\text{d}t} dtdu(t)变为后向差分: u ( k T ) − u [ ( k − 1 ) T ] T \frac{u(kT)-u[(k-1)T]}{T} Tu(kT)−u[(k−1)T],对应: s s s变为 1 − z − 1 T \frac{1-z^{-1}}{T} T1−z−1
特性:
- S负半平面映射到Z平面圆 ( u − 1 2 ) 2 + v 2 < ( 1 2 ) 2 (u-\frac{1}{2})^2+v^2<(\frac{1}{2})^2 (u−21)2+v2<(21)2
- D ( s ) D(s) D(s)稳定,则 D ( z ) D(z) D(z)一定稳定
- 变换前后,稳态增益不变。 D ( s ) ∣ s = 0 = D ( z ) ∣ z = 1 D(s)|_{s=0}=D(z)|_{z=1} D(s)∣s=0=D(z)∣z=1
- 时间响应和频率响应有相当大的畸变
- 变换精度低,使用较少
一阶前向差分法
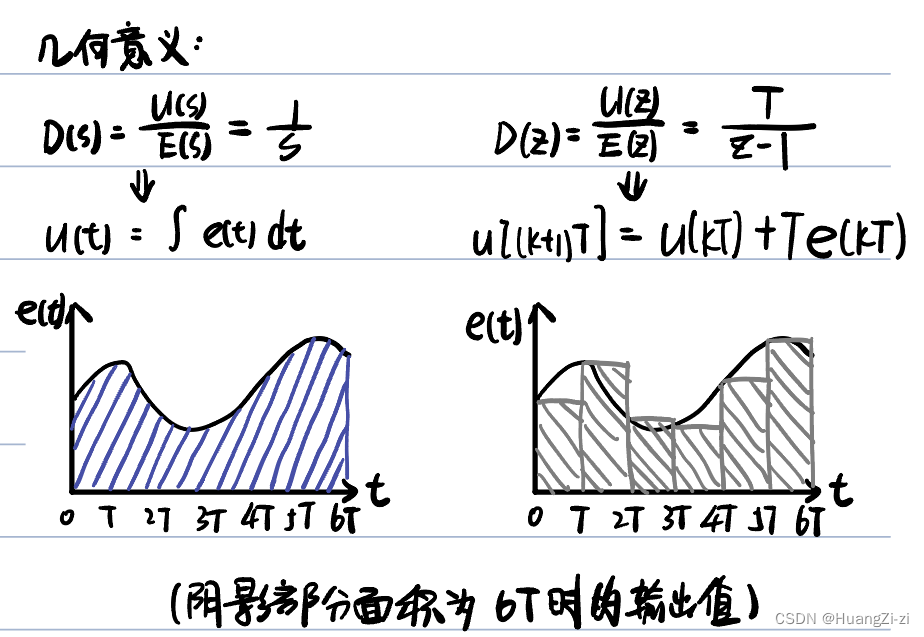
即把微分
d
u
(
t
)
d
t
\frac{\text{d}u(t)}{\text{d}t}
dtdu(t)变为前向差分:
u
[
(
k
+
1
)
T
]
−
u
(
k
T
)
T
\frac{u[(k+1)T]-u(kT)}{T}
Tu[(k+1)T]−u(kT),对应:
s
s
s变为
z
−
1
T
\frac{z-1}{T}
Tz−1
特性:
- S负半平面映射到Z平面 Re ( z ) < 1 \text{Re}(z)<1 Re(z)<1的区域
- Z平面单位圆映射到S平面圆 ( σ + 1 T ) 2 + ω 2 = ( 1 T ) 2 (\sigma+\frac{1}{T})^2+\omega^2 = (\frac{1}{T})^2 (σ+T1)2+ω2=(T1)2。T越小,对应S平面的圆越大,稳定性越好
- D ( s ) D(s) D(s)稳定, D ( z ) D(z) D(z)不一定稳定
- 不能保证稳定性,使用较少
双线性变换法(Tustin)
z
=
e
T
s
=
e
T
s
2
e
−
T
s
2
\displaystyle z=e^{Ts}=\frac{e^{\frac{Ts}2}}{e^{\frac{-Ts}2}}
z=eTs=e2−Tse2Ts
将分子分母分别泰勒展开取前两项,则有:
z
=
1
+
T
s
2
1
−
T
s
2
\displaystyle z=\frac{1+\frac{Ts}{2}}{1-\frac{Ts}{2}}
z=1−2Ts1+2Ts
类比W变换乘以系数
T
2
\frac{T}{2}
2T
对应: s s s变为 2 T z − 1 z + 1 \frac{2}{T}\frac{z-1}{z+1} T2z+1z−1
特性:
-
S负半平面映射到Z平面圆 u 2 + v 2 < 1 u^2+v^2<1 u2+v2<1,S平面虚轴映射到Z平面单位圆上
-
D ( s ) D(s) D(s)稳定, D ( z ) D(z) D(z)一定稳定
-
主要应用于低通环节的离散化。不宜用于高通环节。

-
变换前后,稳态增益不变。 D ( s ) ∣ s = 0 = D ( z ) ∣ z = 1 D(s)|_{s=0}=D(z)|_{z=1} D(s)∣s=0=D(z)∣z=1
-
变换后 D ( z ) D(z) D(z)的阶次不变,且分子分母阶次相同。如果 D ( s ) D(s) D(s)分子比分母低 p p p次,则说明 D ( z ) D(z) D(z)分子中含有 ( z + 1 ) p (z+1)^p (z+1)p
-
使用方便且具有一定精度,工程上使用普遍
零极点匹配法
基本思想:把 D ( s ) D(s) D(s)的零点和极点全部映射到Z平面上
D
(
s
)
D(s)
D(s)原本的零极点按照
z
=
e
s
T
z=e^{sT}
z=esT的方式映射。
D
(
s
)
D(s)
D(s)分子比分母低的阶数用无穷远的零点补全,映射到Z平面
z
=
−
1
z=-1
z=−1处。

其他方法
- Z变换法(脉冲响应不变法)
直接应用Z变换: D ( z ) = Z [ D ( s ) ] D(z)=Z[D(s)] D(z)=Z[D(s)]
这种方法可以保证变换前后脉冲响应不变。但是Z变换比较麻烦、多个环节串连无法单独变换、产生频率混叠、其他特性变化较大。所以应用较少。 - 带零阶保持器的Z变化法(阶跃响应不变法)
D ( z ) = Z [ 1 − e − s T s D ( s ) ] \displaystyle D(z)=Z[\frac{1-e^{-sT}}{s}D(s)] D(z)=Z[s1−e−sTD(s)]
这里的ZOH是假想的,并不真实存在。
这种方法可以保证变换前后阶跃响应不变。但与Z变换有相同的一系列缺点,所以应用较少。
数字PID控制器
模拟PID控制器的离散化
-
PID全量控制
(位置式PID、绝对式PID)

-
PID增量控制
即是仅输出改变量
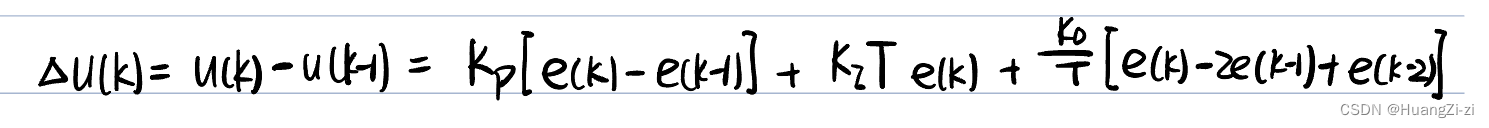
适用于阀、步进电机等具有积分特性的被控对象。
数字PID的改进
-
抗积分饱和
- 当输出的控制量很大,超出DA的转换范围或者超过执行机构的执行范围(例如,控制器输出25,但DAC只能输出5;控制器输出120,但阀门只能开到100)此时尽管控制器持续运算、输出,但执行机构没有动作,称为积分饱和。发生积分饱和时,相当于断开闭环控制系统。
- 遇限削弱积分法
当控制量进入饱和区,只执行削弱积分项的积分

- 饱和停止积分法
当控制量进入饱和区,不执行积分。优点是简单易行。缺点是不易使系统退出饱和。

-
防积分整量化误差
- 积分项的数值太小,可能在计算机的有限字长中无法表示,发生积分项丢失的现象
- 解决方法:用双字长存储积分运算结果。当结果小于单字长时,加到低位单元。直到低位单元进位到高位单元。(输出只输出高位单元。相当于扩展了字长,能够表示的最小值变小了)
-
微分算法改进
- 微分放大噪声的作用,极易引入高频干扰
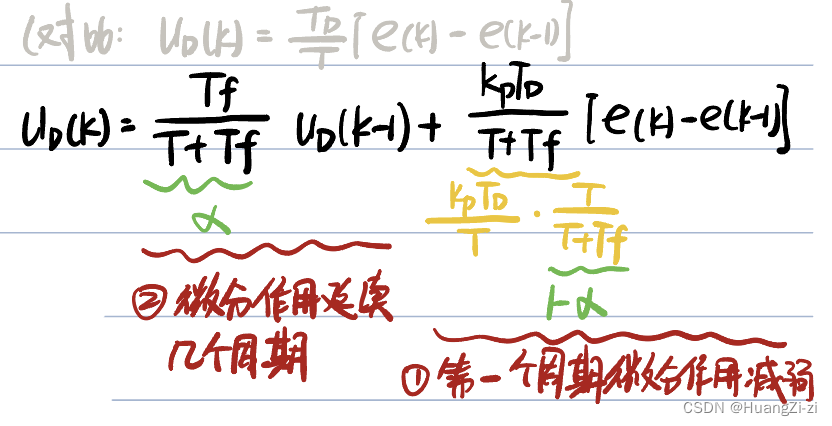
- 不完全微分PID:
即使用带惯性环节的实际微分器。
s → s 1 + T f s s\to\frac{s}{1+T_f s} s→1+Tfss
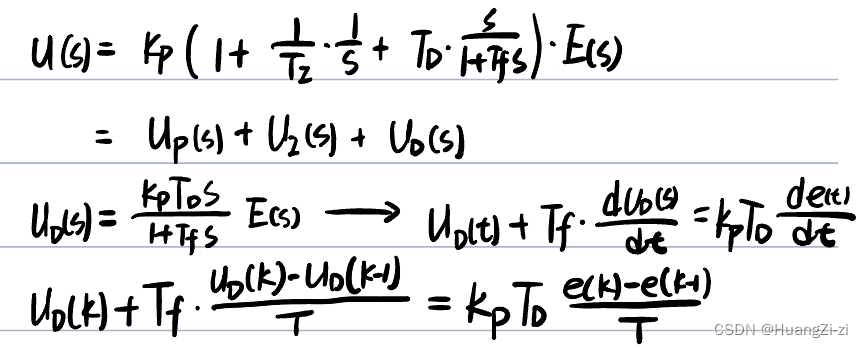
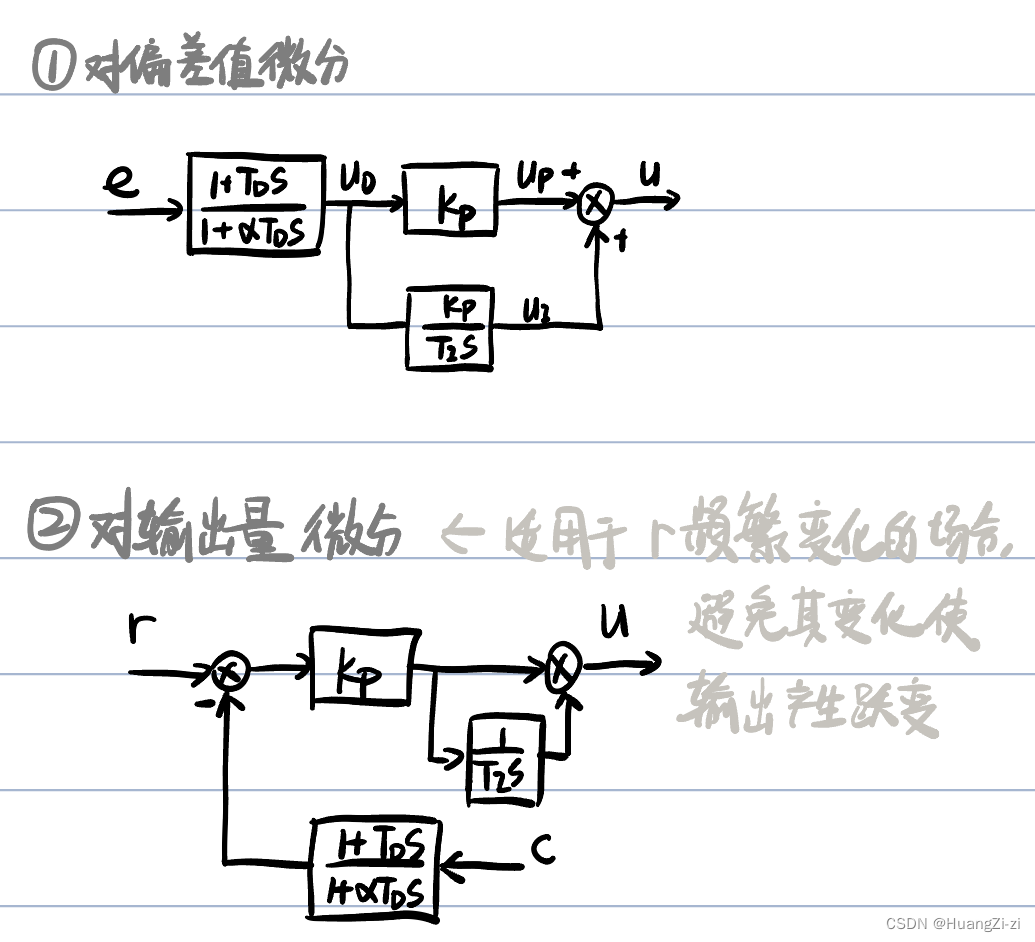
- 微分先行PID
即把微分提前到比例和积分运算之前
-
带非灵敏区
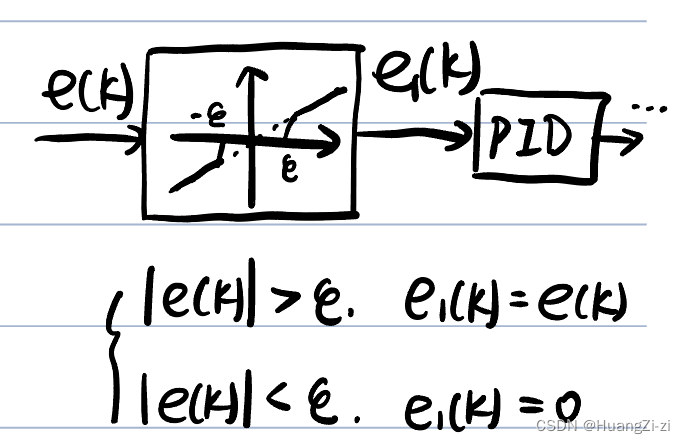
偏差小的时候断开控制。可以节约能源、保护执行机构
PID控制各环节的作用
- 比例环节:
随 K p K_p Kp的增大,超调量增大,响应速度加快,稳态误差减小(但不能消除)
如果 K p K_p Kp偏大,系统输出震荡次数变多,调节时间加长
如果 K p K_p Kp过大,将导致系统不稳定 - 积分环节:
随 T I T_I TI的增大,超调量减小,响应速度减慢,可以完全消除稳态误差
如果 T I T_I TI过大,积分作用削弱,对系统动态性能的影响减小,但可能无法消除静态误差
如果 T I T_I TI过小,系统会不稳定 - 微分环节:
选择合适的 T D T_D TD将使系统的超调量减小,调节时间缩短,允许加大比例控制。
T D T_D TD太大或太小,都会适得其反
PID参数的整定
扩充临界比例度法
- 选择采样周期。通常取被控对象纯滞后的 1 10 \frac1{10} 101
- 将PID控制器设置为纯P,减小比例度 ( δ = 1 K p ) (\delta=\frac{1}{K_p}) (δ=Kp1),直到系统等幅震荡。记录临界比例度 δ k \delta_k δk以及临界震荡周期 T k T_k Tk
- 选择控制度
- 查表,确定 T , K p , T I , T D T, K_p, T_I, T_D T,Kp,TI,TD的值
- 试运行,如果性能不满意,可进一步调节参数
控制度 = ∫ 0 ∞ [ e 2 ( t ) d t ] D D C ∫ 0 ∞ [ e 2 ( t ) d t ] A n a l o g \displaystyle 控制度=\frac{\int_0^\infty [e^2(t)\text{d}t]_{DDC}}{\int_0^\infty[e^2(t)\text{d}t]_{Analog}} 控制度=∫0∞[e2(t)dt]Analog∫0∞[e2(t)dt]DDC,越接近1,说明数字控制器和模拟控制器性能越接近。是一个根据需要选定的值。
整定参数表:
| 控制度 | 控制规律 | T / T k T/T_k T/Tk | K P δ k K_P \delta_k KPδk | T I / T k T_I/T_k TI/Tk | T D / T k T_D/T_k TD/Tk |
|---|---|---|---|---|---|
| 1.05 | PI | 0.03 | 0.53 | 0.88 | - |
| 1.05 | PID | 0.014 | 0.63 | 0.49 | 0.14 |
| 1.20 | PI | 0.05 | 0.49 | 0.91 | - |
| 1.20 | PID | 0.043 | 0.47 | 0.47 | 0.16 |
| 1.50 | PI | 0.14 | 0.42 | 0.99 | - |
| 1.50 | PID | 0.09 | 0.34 | 0.43 | 0.20 |
| 2.00 | PI | 0.22 | 0.36 | 1.05 | - |
| 2.00 | PID | 0.16 | 0.27 | 0.40 | 0.22 |
扩充阶跃响应曲线法
- 控制器不接入系统,将被控量调至给定值附近,并使其稳定。然后测被控对象的单位阶跃响应曲线。
- 在曲线的拐点处作切线,求出纯滞后 τ \tau τ和时间常数 T m T_m Tm
- 选择控制度
- 查表,确定 T , K p , T I , T D T, K_p, T_I, T_D T,Kp,TI,TD的值
整定参数表:
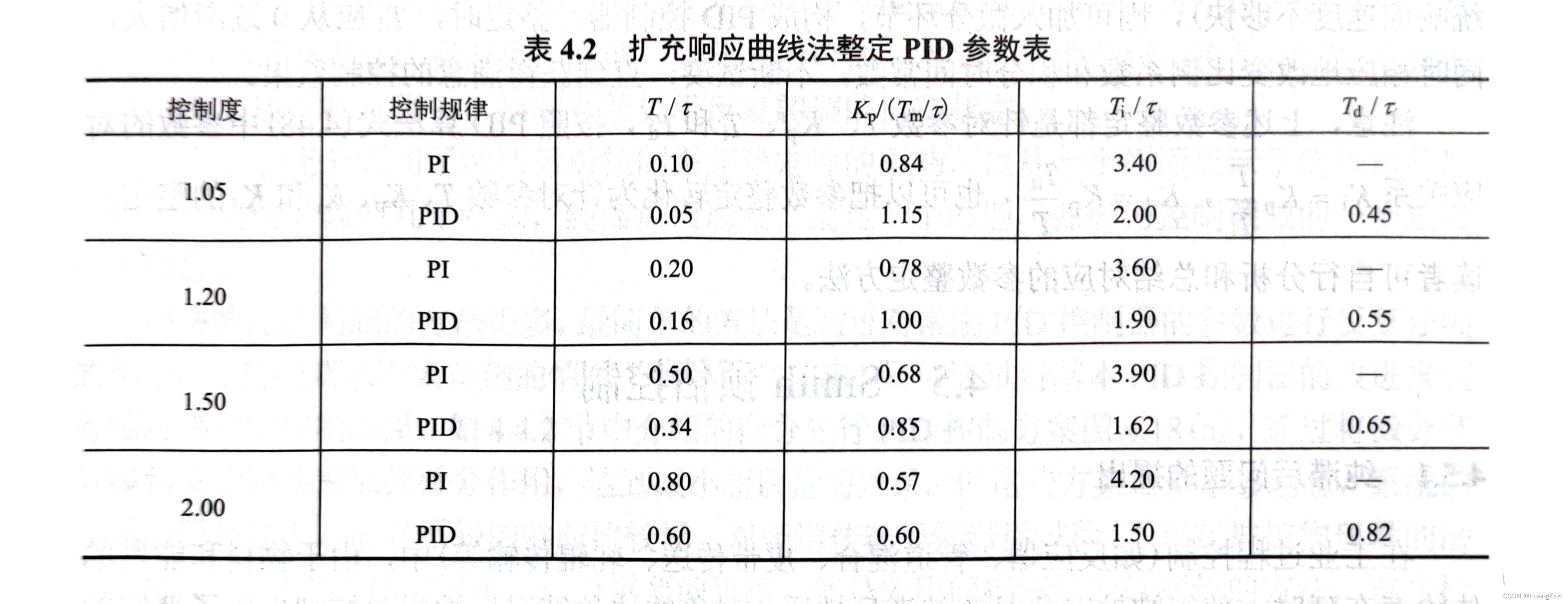
「图源:刘建昌_计算机控制系统」
PID控制器的无扰切换
实际运行中,需要在自动与手动控制模式之间进行切换。要求切换时不对调节过程带来大的冲击。
在手动控制时,PID算法应该继续计算,减小切换回自动时的冲击。

Smith预估控制
适用于大滞后或者大延迟
当
τ
/
T
m
>
0.3
\tau /T_m>0.3
τ/Tm>0.3,就可以认为是大滞后或大延迟。如果
τ
/
T
m
>
0.5
\tau /T_m>0.5
τ/Tm>0.5,一般就需要特殊处理。因为常规PID 会使系统稳定性变差甚至产生震荡。
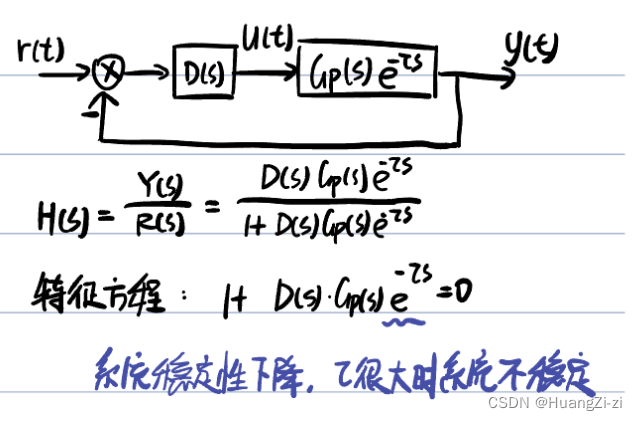
设计纯滞后补偿控制系统

在计算机控制系统中实现纯滞后补偿:
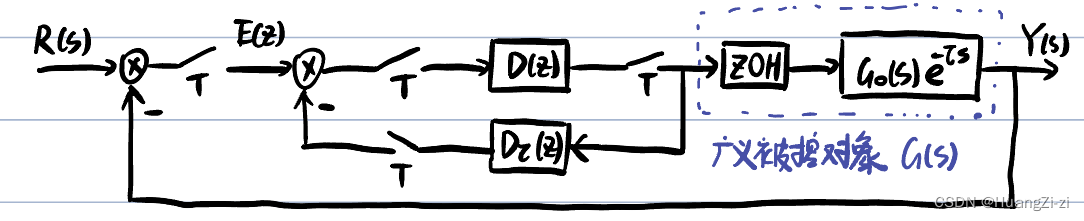
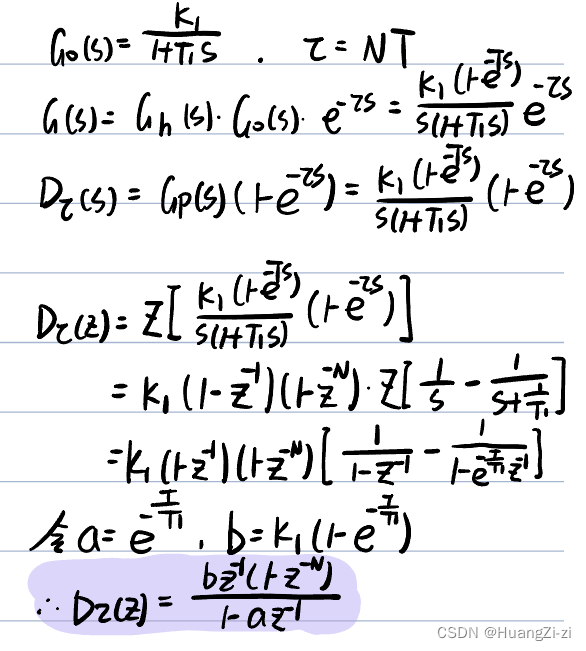
Smith预估器的编排结构
几种不同的控制算法的编排结构:

研究参数
a
k
a_k
ak变化对于极点的影响:

将上式称为灵敏度公式,其可以表示某个分母参数变化引起某个极点变化的灵敏度。(越小越不灵敏)
可以看出,
k
k
k越大,对根的影响最大。(稳定时
∣
p
i
∣
<
1
|p_i|<1
∣pi∣<1)
且影响与极点之间的距离成反比。

Smith预估器采用串联型结构:
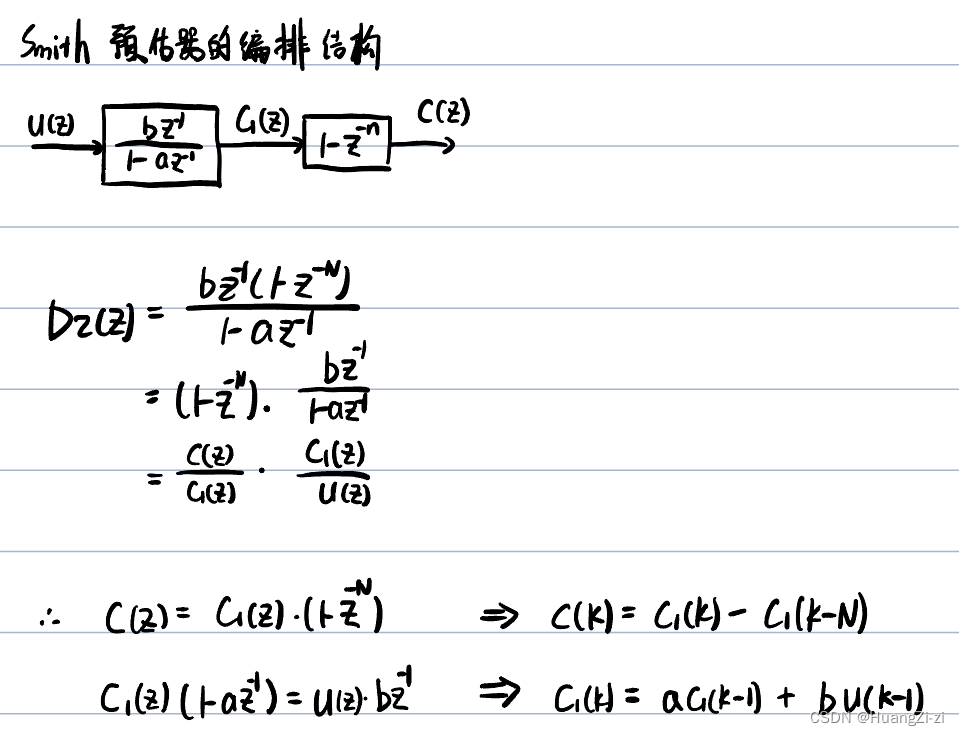

![[强化学习]学习路线和关键词拾零](https://img-blog.csdnimg.cn/d38930816c1045968b03d2844d6bad8c.png)