Multiple View Geometry

本文主要介绍计算机视觉中，光流法Optical Flow Method，Lucas-Kanade方法的约束，CV中光流的约束分析，包括了亮度不变约束，速度向量计算等方法。

1. Optical Flow Estimation

Optical Flow is suitable for small deformation, small displacement. Finding correspondence and tracking.

2. The Lucas-Kanade Method

2.1 Brightness Constancy Assumption

Let $x(t)$ denote a moving point at time $t$, and $I(x,t)$ a video sequence, then:
$$I(x(t),t)=Const.\forall t.$$
i.e., the brightness of point $x(t)$ is constant. Therefore the total time derivate must be zero:
$$\frac{d}{d(t)}I(x(t),t)=\nabla I^T(\frac{dx}{dt})+\frac{\partial I}{\partial t}=0$$
This constraint is often called the optical flow constraint. The desired local flow vector (velocity) is given by $v=\frac{dx}{dt}$.

Prof: the derivative of $\frac{dI}{dx}\frac{dx}{dt}$, where the first component is $\nabla I$ is$(\frac{\partial I}{\partial x},\frac{\partial I}{\partial y}{)}^T$.

So, the first component can be described as: this is the flow vector $v$, (which represents the movement direction), projection on the image gradient $\nabla I$ .

$\nabla I$ Is the spatial brightness derivative, $\frac{\partial I}{\partial t}$ is the temporal brightness derivative, $\frac{dx}{dt}$ is the velocity vector.

2.2 Constant motion in a neighborhood

One assumes that $v$ is constant over a neighborhood window $W(x)$ of the point $x$:
$$\nabla I(x^{\prime },t{)}^{T}v+\frac{\partial I}{\partial t}(x^{\prime },t)=0,\forall x^{\prime }\in W(x).$$

2.3 Compute the velocity vector

Compute the best velocity vector $v$ for the point $x$ by minimizing the least square error:
$$E(v)={\int }_{W(x)}{\left|\nabla I(x^{\prime },t{)}^{T}v+I_t(x^{\prime },t)\right|}^{2}d{x}^{\prime }.$$
Setting the derivative to zero we obtains:
$$\frac{dE}{dv}=2Mv+2q=0$$

2.4 KLT tracker

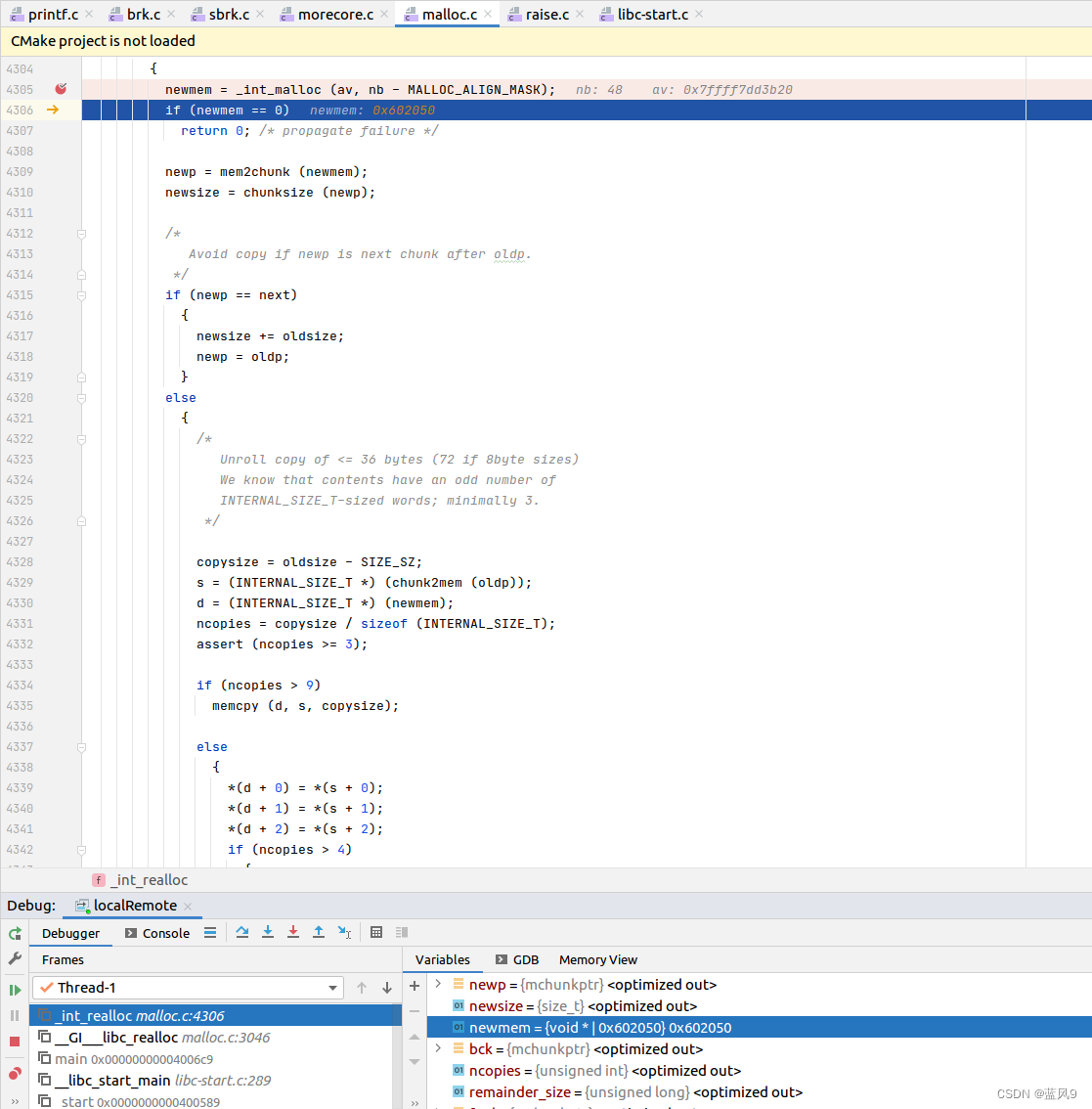
KLT tracker. A simple feature tracking algorithm. However, this is not reliable. When the contrast or the image pixel deviation in a low manner, the gradient is easy to be zero, which make the $M(x)$ is easy to un-invertible, which can not guarantee to be larger than a threshold. So, these tracking points are no longer useful, we should find another pixel points to initial as new tracking points.

Even $det(M)\ne 0$, dose not guarantee robust estimates of velocity, the inverse of $M(x)$ may not stable if $det(M)$ is very small.

3. Robust feature point extraction: Harris Corner detector.

So, to guarantee robust estimation of velocity, a robust feature point extraction algorithm has been proposed. Named Harris Corner extraction.

4. Eliminate the brightness changes.

1. Since the motion is no longer translational, one need to generalize the motion model for window $W(x)$, so, we can use affine motion model or homograph motion model.

2. Robust to illumination changes.

   We can use Normalized Cross Correlation to reduce the intensity changes.