- gmm建模方差使用对角矩阵的前提是假设特征之间相互独立,使用full或者block-diagonal矩阵可以对相关性的特征建模,但是参数增多。为了解决使用这个问题,有两种方法:
- feature-space 使用DCT或者LDA去相关
- model-space 不同的模型可以使用不同的转换,更灵活
- semi-tied covariance matrices(STC)是model-space里面的一种形式,也是为了解决使用full covariance的参数量大的问题。相比于full covariance,这种方法的每个高斯分量有两个方差矩阵:

- LDA:
- 线性判别分析,是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。
- LDA的核心思想为投影后类内方差最小,类间的方差最大。简单来说就是同类的数据集聚集的紧一点,不同类的离得远一点
- LDA算法流程:

- MLLT:
- 最大似然线性变换
- 是一个平方特征变换矩阵,用于建模方差,解决full convariance的参数量大的问题。
- 相比于full convariance,该方法的每个高斯分量有两个方差矩阵:

- kaldi中的train_lda_mllt.sh:
- 主要功能:MFCC→CMVN→Splice→LDA→MLLT→final.matMFCC→CMVN→Splice→LDA→MLLT→final.mat ,然后训练GMM。
- 该程序的执行流程为:

- 计算类内散度矩阵:
- 类内散度矩阵:为了最小化类内的可变性,类内分散。
- 计算:

协方差矩阵计算:从每个观测值中减去平均值,然后用矩阵的转置执行矩阵乘法后计算平均值。
- 计算类间散度矩阵:
- 增加类间差异,类间分散。
- 计算(不同类均值相减并乘上转置):

- 计算类内散度矩阵:
STC/MLLT--学习笔记
news2026/2/16 12:43:51
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/44009.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
连续时间系统的时域分析
一.微分方程的求解 1.求微分方程的齐次解 (1)写出特征方程并求解 2.写出齐次解 2.求微分方程的特解 已知 (1)根据表2-2,写出特解函数 (2)带入并求解 3.完全解 二.微分方…
基于GRU与注意力机制实现法语-葡萄牙语的翻译详细教程 数据+代码
本教程通过机器翻译的例子来介绍和实现一个简单的机器翻译方法,机器翻译是指将一段文本从源语言(如语言A)自动翻译到目标语言(如语言B)。本教程通过加载和预处理数据、构造编码器和解码器、训练模型、结果评价得到一个可以应用的机器翻译工具。
1.2 任务描述
神经机器翻译方…
uni-app 介绍及使用
一、什么是uni-app uni-app由dcloud公司开发的多端融合框架,是一个使用 Vue.js 开发所有前端应用的框架,开发者编写一套代码,可发布到iOS、Android、Web(响应式)、以及各种小程序(微信/支付宝/百度/头条/飞…
单文件组件环境配置步骤---vue-cli版
因为浏览器只认识:html、css、js文件,其他一概不认识;
所以要把单文件组件的vue文件转化为上面浏览器能认识的文件;
有两种环境配置途径:
第一种就是:配置webpack环境,要下载很多东西&#x…
灰色预测GM(1.1)模型及matlab程序负荷预测
灰色GM(1.1)预测模型 GM(1.1)模型由包含单一变量的一阶微分方程构成的模型,是灰色模型中最常用的模型。 设有负荷变量为的原始数据列: (3-1) 生成一阶累加数据列: (3-2) 其中 (3-3) 一阶微分方程的解呈指数增长形式,…
URLDNS利用链分析
目录
前言: (一)原理
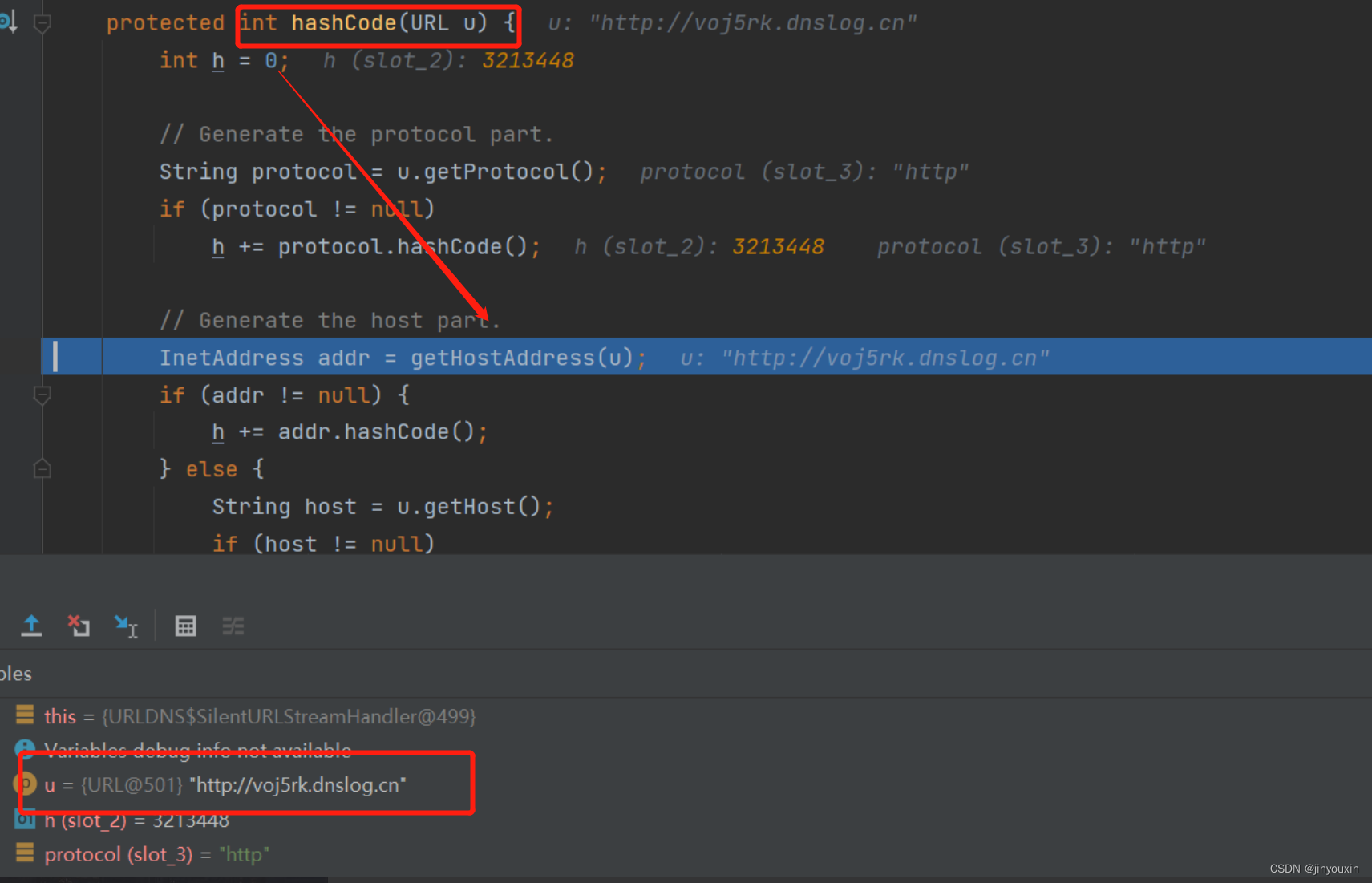
(二)利用链 再来分析 URLDNS.java 这个文件,并且在入口处设置断点进行调试:
(三) POC
参考资料 前言: URLDNS是Java反序列化中比较简单的一个链…
引擎入门 | Unity UI简介–第2部分(1)
欢迎回来! 在这个三部分教程系列的第二部分中,你将学习如何在用户界面中加入动画。
在上一个部分中你学习并创建了一个带有两个按钮的场景,也学会了如何使用图像、按钮和文本UI控件,并学习了RectTransform、Anchors和Pivots等核心概念&#…
元宇宙的核心技术之我见
14天学习训练营导师课程: 张子良《 元宇宙体系结构、关键技术和实践探索》
前言 提起元宇宙,相比读者都有所耳闻,而且元宇宙最近两年时间里异常的火,堪比之前的人工智能的火爆场景,甚至要超越人工智能的火爆度了。但是…
kubernetes namespace pod label deployment介绍与命令
kubernetes namespace pod label deployment 介绍与命令
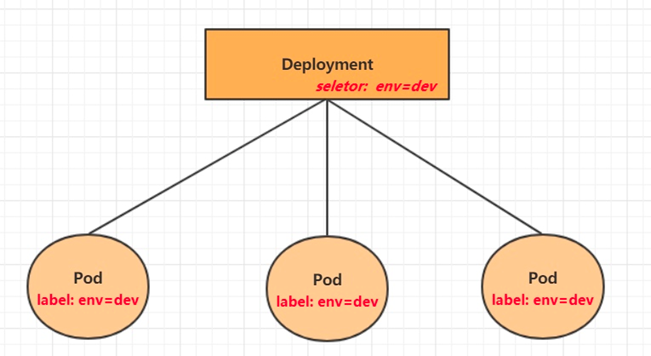
1: namespace
Namespace是kubernetes系统中的一种非常重要资源,它的主要作用是用来实现多套环境的资源隔离或者多租户的资源隔离。 默认情况下,kubernetes集群中的所有的Pod都是可以…
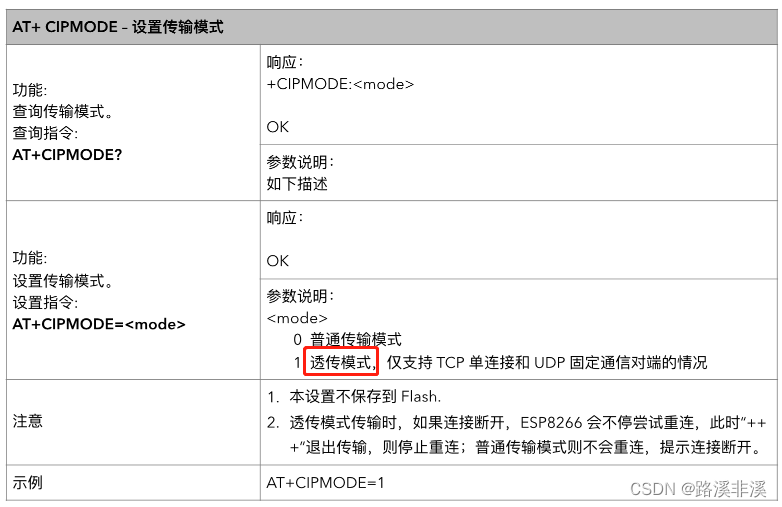
STM32实战总结:HAL之wifi
关于无线传输的基础知识,参考: 无线通信技术概览_路溪非溪的博客-CSDN博客 学了这么多,发现信息技术主要就是数据的存储、处理以及传输这几个过程。通过各种各样的技术,来实现这几个目标。 wifi模块 现在常用的是wifi模块…
今天面了个腾讯拿38K出来的,让我见识到了基础的天花板
各大论坛和社区里也看见不少小伙伴慷慨地分享了常见的面试题和八股文,为此咱这里也统一做一次大整理和大归类,这也算是划重点了。
俗话说得好,他山之石,可以攻玉,多看多借鉴还是有帮助的,这次腾讯也在疯狂…
自动化测试如何实施落地?详细教程来了
目录 前言
落地前:分析因素
开展前:评估价值
落地过程:解决问题
推广运营:关注反馈&输出价值
文末总结
重点:配套学习资料和视频教学 前言
这篇文章, 就聊聊自动化项目如何落地,以及…
25. [Python GUI] PyQt5中拖放的基本原理
PyQt5的拖放
拖放涉及到的主要的一些类如下所示: 一、拖放的基本原理
1.1 拖放的动作
拖放操作包括两个动作:
拖动(drag)放下(drop 或称为放置)。
当被拖动时拖动的数据会被存储为 MIME 类型的对象, MIME 类型使用 QMimeData 类来描述。…
C++——new和delete关键字
什么是new和delete
new和delete不是函数,和sizeof一样都是C定义的关键字,不同的是sizeof在编译时就可以确定其返回值,而new和delete相对复杂
示例
string *ps new string("hello world");如果换做c语言,上面这句话就…
数据库——数据库备份与恢复
目录 原因: 数据库的备份与恢复: 1、使用MySQLdump命令备份 2、恢复数据库 表的导入和导出 1、表的导出 2、表的导入 原因: 尽管采取了一些管理措施来保证数据库的安全,但是不确定的意外情况总是有可能造成数据的损失,…
数据库理论 05 关系数据库设计——基于《数据库系统概念》第七版
通过E-R图转换得出一组关系模式后 **选择1:**把一些关系模式合并为更大的关系 —— 会产生过多的数据冗余
inst_dept(ID, name, salary, dept_name, building, budget)如果通过E-R模型转换得出如下两个关系模式
sec_class(sec_id, building, room_number) and
se…
2023最新SSM计算机毕业设计选题大全(附源码+LW)之java计算机专业建设管理系统3286d
面对老师五花八门的设计要求,首先自己要明确好自己的题目方向,并且与老师多多沟通,用什么编程语言,使用到什么数据库,确定好了,在开始着手毕业设计。
1:选择课题的第一选择就是尽量选择指导老师…
ThreadLocal源码解析 1.运行原理
ThreadLocal源码解析—运行原理
简介
ThreadLocal 类用来提供线程内部的局部变量,这种变量在多线程环境下访问(通过 get 和 set 方法访问)时能保证各个线程的变量相对独立于其他线程内的变量,分配在堆内的 TLAB 中。
ThreadLoc…
【Mybatis编程:根据若干个id批量删除相册(动态SQL)】
目录
1. 执行的SQL语句
2. 在AlbumMapper.java接口添加抽象方法
3. 在AlbumMapper.xml中配置以上抽象方法映射的SQL语句
4. 标签书写规范 1. 执行的SQL语句
需要执行的SQL语句大致是:
delete from pms_album where id? or id? or ... id?
delete from pms…
《机器学习实战》10.K-均值聚类算法
目录
利用K-均值聚类算法对未标注数据分组
K-均值聚类算法
2 使用后处理来提高聚类性能
3 二分K-均值算法
4 示例:对地图上的点进行聚类
4.1 Yahoo!PlaceFinder API
4.2 对地理坐标进行聚类
5 本章小结 本章涉及到的相关代码和数据
利用K-均值聚…
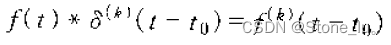








![25. [Python GUI] PyQt5中拖放的基本原理](https://img-blog.csdnimg.cn/img_convert/0ca215457f402ef0a575339b54ba0697.png)






