常见的激活函数介绍

激活函数是神经网络中的重要组成部分，它决定了神经元的输出。在神经网络的前向传播中，输入数据被传递给神经元，经过加权和和激活函数的计算后，得到神经元的输出。

本文将介绍几种常见的激活函数，它们的定义、特点和应用场景。

Sigmoid函数

Sigmoid函数是一种常用的激活函数，它将输入映射到一个介于0和1之间的值。它的公式如下：
$$f(x)=\frac{1}{1+e^{-x}}$$

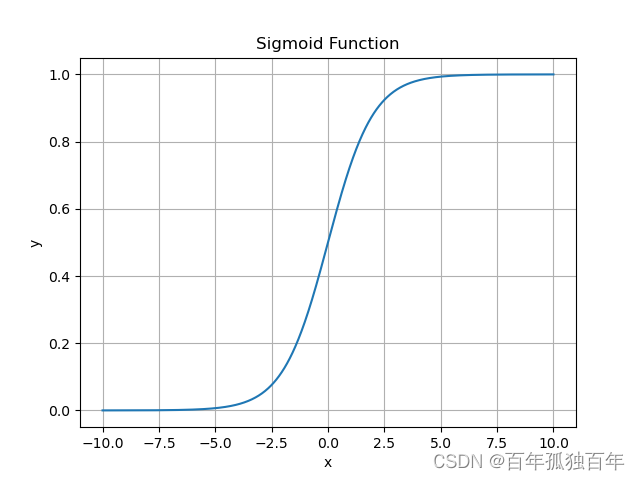
Sigmoid函数具有平滑且连续的输出，这使得它在某些情况下非常有用。例如，它常被用于二分类问题中，因为它的输出可以被解释为“概率”。

但是，Sigmoid函数在输入较大或较小的情况下，输出会非常接近于0或1，这会导致梯度消失的问题。因此，在深度神经网络中，Sigmoid函数不太常用。

ReLU函数

ReLU函数是一种非常简单和有效的激活函数。它的公式如下：
$$f(x)=\max (0,x)$$

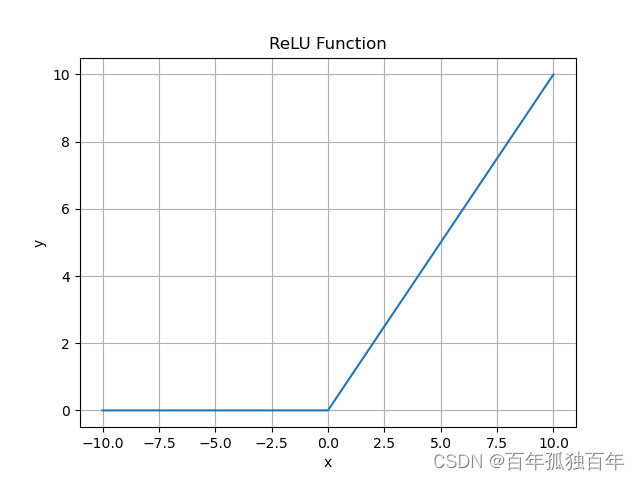
ReLU函数的输出为正数，负数则为0。这使得它在解决梯度消失的问题上非常有效，同时也能够加速模型的训练速度。

ReLU函数在许多深度神经网络中广泛应用，但它也有一些问题。例如，当输入为负数时，梯度为0，这被称为“死亡ReLU”问题。此外，在某些情况下，ReLU函数可能导致“梯度爆炸”问题。

LeakyReLU函数

LeakyReLU函数是对ReLU函数的一种改进。它的公式如下：
$$f(x)=\{\begin{array}{ll}x& \text{if }x>0\\ ax& \text{otherwise}\end{array}$$

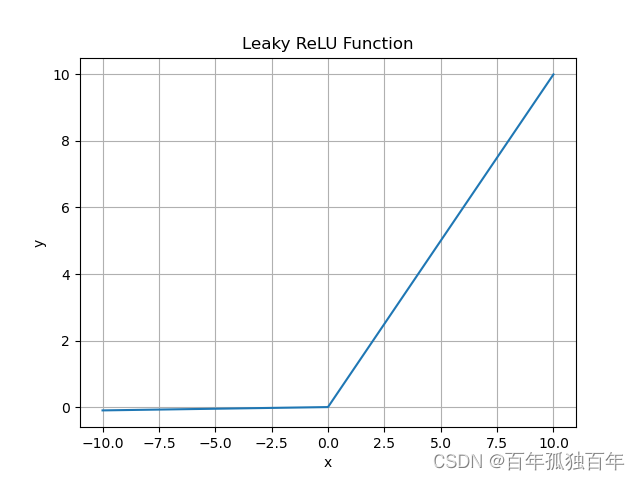
其中，$a$是一个小的常数，通常为0.01。LeakyReLU函数在输入为负数时，不会完全变为0，而是将输入乘以一个小的常数。这使得LeakyReLU函数能够在解决“死亡ReLU”问题的同时，保持ReLU函数的优点。

Tanh函数

Tanh函数是另一种常见的激活函数，它将输入映射到一个介于-1和1之间的值。它的公式如下：
$$f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

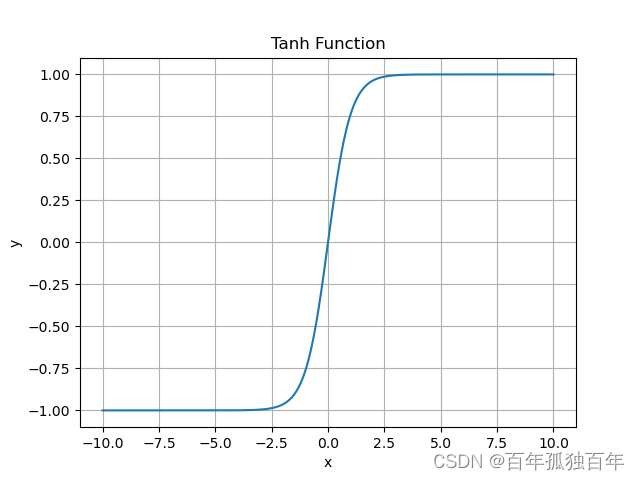
Tanh函数与Sigmoid函数类似，但它的输出范围是[-1,1]。Tanh函数在某些情况下比Sigmoid函数更好，因为它的输出可以被解释为正负的概率。但是，Tanh函数也有梯度消失的问题，类似于Sigmoid函数。

Softmax函数

Softmax函数是一种用于多分类问题的激活函数。它将输入映射到一个概率分布上，使得所有输出值之和为1。Softmax函数的公式如下：

$$f(x_i)=\frac{e^{x_i}}{{\sum }_{j=1}^k{e}^{x_j}}$$
其中，$k$是输出的类别数。 Softmax函数常被用于多分类问题中，因为它可以将神经网络的输出解释为每个类别的概率。

# 示例代码
import numpy as np
import matplotlib.pyplot as plt

def softmax(x):
    exp_x = np.exp(x)
    return exp_x / np.sum(exp_x)

x = np.array([1, 2, 3, 4, 5])
y = softmax(x)

print(y)

# 输出如下
[0.01165623 0.03168492 0.08612854 0.23412166 0.63640864]

总结

本文介绍了几种常见的激活函数，它们分别是Sigmoid函数、ReLU函数、LeakyReLU函数、Tanh函数和Softmax函数。每种激活函数都有其独特的特点和应用场景，选择合适的激活函数可以提高神经网络的性能。