1、前言

​ 当分析数据时，如果我们找的不是直线或者超平面，而是一条曲线，那么就可以用多项式回归来分析和预测。

2、定义及公式

​ 多项式回归可以写成：
$$Y_i={\beta }_0+{\beta }_1{X}_i+{\beta }_2{X}_i^2+...+{\beta }_k{X}_i^k$$
​ 例如二次曲线：
$$Y=aX+b{X}^2+c$$

3、案例代码

1、数据解析

​ 首先有1961年至2017年我国地表温度变化和温室气体排放量的时间序列数据，前十条数据如下。

temp	emissions
0.257	5635838102
-0.142	6075180207
0.288	6510697811
-0.028	6946401541
0.076	7421082166
0.18	7942541079
-0.286	8374764636
-0.414	8842570279
-0.22	9418514950

2、绘制散点图

​ 对于该数据我们先通过绘制散点图，这可以看出该数据适用于什么模型。

import matplotlib.pyplot as plt
import xlrd
import numpy as np
# 载入数据，打开excel文件
ExcelFile = xlrd.open_workbook("sandian.xls")
sheet1 = ExcelFile.sheet_by_index(0)
x = sheet1.col_values(0)
y = sheet1.col_values(1)
# 将列表转换为matrix
x = np.matrix(x).reshape(48, 1)
y = np.matrix(y).reshape(48, 1)

# 划线y
plt.title("Epidemic and Dow Jones data analysis")
plt.xlabel("new cases")
plt.ylabel("Dow Jones Volume")
plt.plot(x, y, 'b.')
plt.show()

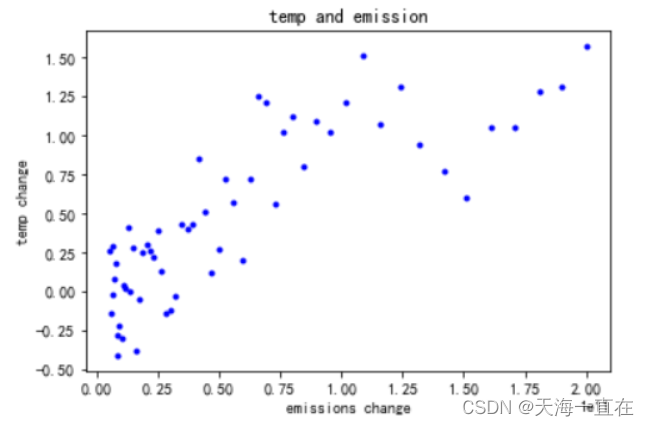
​ 上述使用xlrd方式不建议使用，简单了解即可，正常我们会使用下述更为方便且稳定的pandas来读取csv文件，这会大大简洁我们的代码并减少工作量。当然结果也是一样的。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd


x = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']
# 划线y
plt.title("temp and emission")
plt.xlabel("emissions change")
plt.ylabel("temp change")
plt.plot(x, y, 'b.')
plt.show()

​ 如图所示很明显，在排放量变化达到1.5(1e11)时，斜率发生了改变，因此我们可以判断这是一个多项式模型。

3、多项式回归、拟合

​ 通过散点图的趋势，我们首先选择拟合3次来防止过拟合和欠拟合。

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.metrics import r2_score
from matplotlib.font_manager import FontProperties  # 导入FontProperties

font = FontProperties(fname="simhei.ttf", size=14)  # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =False

x = pd.read_csv('china.csv')['emissions']
y = pd.read_csv('china.csv')['temp']

# 进行多项式拟合（这里选取3次多项式拟合）
z = np.polyfit(x, y, 3) # 用3次多项式拟合
 
# 获取拟合后的多项式
p = np.poly1d(z)
print(p)  # 在屏幕上打印拟合多项式
 
# 计算拟合后的y值
yvals=p(x)
 
# 计算拟合后的R方，进行检测拟合效果
r2 = r2_score(y, yvals)
print('多项式拟合R方为:', r2)
 
# 计算拟合多项式的极值点。
peak = np.polyder(p, 1)
print(peak.r)

# 画图对比分析
plot1 = plt.plot(x, y, '*', label='初始值', color='red')
plot2 = plt.plot(x, yvals, '-', label='训练值', color='blue',linewidth=2)
 
plt.xlabel('温室气体排放量',fontsize=13, fontproperties=font)
plt.ylabel('温度变化',fontsize=13, fontproperties=font)
plt.legend(loc="best")
plt.title('中国温室气体排放量与地表温度变化的关系')
plt.show()

​ 最后结果如下图

           3             2
3.002e-34 x - 1.351e-22 x + 2.284e-11 x - 0.2613
多项式拟合R方为: 0.7468687074304835
[1.50000065e+11+5.34488173e+10j 1.50000065e+11-5.34488173e+10j]

​ 我们发现，这并不符合我们的预期，因为温室气体排放量在1.5(1e11)时，散点图趋势有明显的凹陷，而使用三次拟合并不能让曲线拟合到散点上。所以我们将 z = np.polyfit(x, y, 4)中的3改为4，来进行四次拟合。

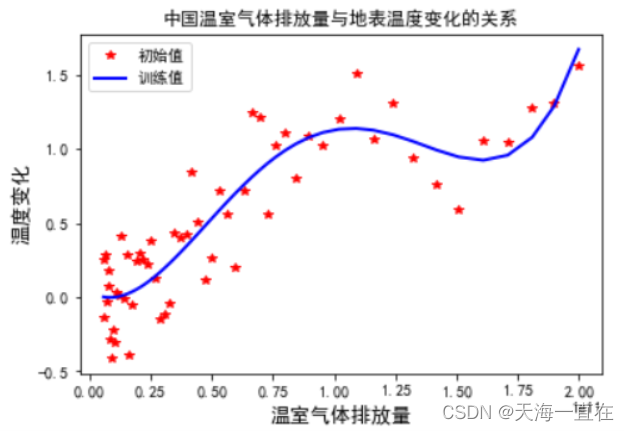
​ 这样就达到了我们的预期效果，并输出我们的多项式回归公式。

           4             3             2
1.702e-44 x - 6.273e-33 x + 6.634e-22 x - 9.696e-12 x + 0.03595
多项式拟合R方为: 0.7962406171380259
[1.60734484e+11 1.07514523e+11 8.24309615e+09]

​ 我们可以得到数学模型：
$$Y=1.702\ast 10^{-44}X-6.273\ast 10^{-33}X+6.634\ast 10^{-22}X-9.696\ast 10^{-12}X+0.03595$$

4、注意事项

from matplotlib.font_manager import FontProperties  # 导入FontProperties
font = FontProperties(fname="simhei.ttf", size=14)  # 设置字体
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] =False

​ 这些代码用于显示汉字标题，这需要你的本机中有一个汉字字体文件，simhei.ttf或其他字体文件。

​ 如果需要引入，在第二行中指定文件路径。