朋友论文需要用到层次分析法。于是回顾了一下。

相关资料推荐

层次分析法(AHP)
层次分析法（AHP）详细版本
用人话讲明白AHP层次分析法（非常详细原理+简单工具实现）

层次分析法的流程图

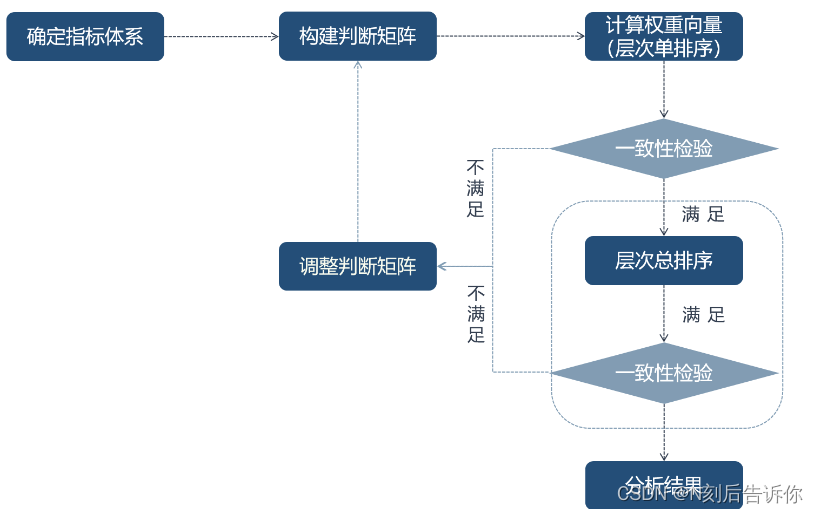
构建层次结构模型(目标-准则-方案层)

深入分析实际问题，将有关因素自上而下分层。
下面以“旅游地选择问题”为例。

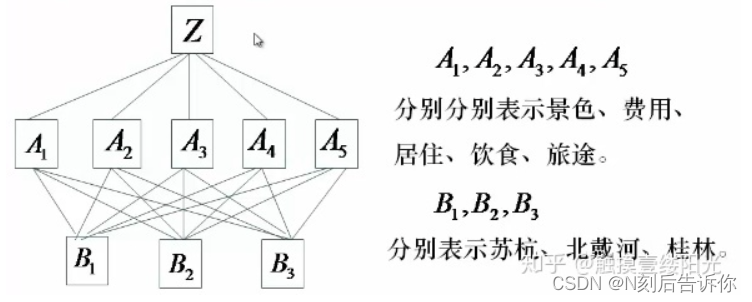
这里目标层和方案层之间只有一个准则层。其实可以有多个准则层。

构造各层次中的所有判断(成对比)矩阵

用成对比较法和1-9尺度，构造各层对上一层每一因素的判断较矩。

准则层对目标层的判断矩阵

A_Z = np.array([[1, 1/2, 4, 3, 3], 
              [2, 1, 7, 5, 5],
              [1/4, 1/7, 1, 1/2, 1/3],
              [1/3, 1/5, 2, 1, 1],
              [1/3, 1/5, 3, 1, 1]])

方案(措施)层对准则层的判断矩阵

B_A1 = np.array([[1, 2, 5], 
              [1/2, 1, 2],
              [1/5, 1/2, 1]])
B_A2 = np.array([[1, 1/3, 1/8], 
              [3, 1, 1/3],
              [8, 3, 1]])
B_A3 = np.array([[1, 1, 3], 
              [1, 1, 3],
              [1/3, 1/3, 1]])
B_A4 = np.array([[1, 3, 4], 
              [1/3, 1, 1],
              [1/4, 1, 1]])
B_A5 = np.array([[1, 1, 1/4], 
              [1, 1, 1/4],
              [4, 4, 1]])

层次单排序及其一致性检验

层次单排序：获得同一层次因素对上一层次某因素相对重要性的排序权值的过程。
层次单排序需要经过一致性检验。

• 一致性指标$CI$：$CI=\frac{\lambda -n}{n-1}$，$\lambda$是最大特征值
• 随机一致性指标$RI$：查表或者自己计算。(下面是表)
  
• 一致性比率$CR$：$CR=\frac{CI}{RI}$

$CR<0.1$认为通过一致性检验。

下面以”准则层对目标层的判断矩阵“为例

计算最大特征值和对应归一化特征(权)向量

def HSA(mat): # Hierarchical Single Arrangement
    index = np.argmax(np.linalg.eig(mat)[0])
    max_eig = np.round(np.real(np.linalg.eig(mat)[0][index]), 3)
    q = np.real(np.linalg.eig(mat)[1][:, index]) # 权向量
    normal_q = np.round(q/sum(q), 5)
    return max_eig, normal_q

print(f"A_Z的最大特征值为{HSA(A_Z)[0]}, 对应归一化权向量为{HSA(A_Z)[1]}" )
print(f"B_A1的最大特征值为{HSA(B_A1)[0]}, 对应归一化权向量为{HSA(B_A1)[1]}" )
print(f"B_A2的最大特征值为{HSA(B_A2)[0]}, 对应归一化权向量为{HSA(B_A2)[1]}" )
print(f"B_A3的最大特征值为{HSA(B_A3)[0]}, 对应归一化权向量为{HSA(B_A3)[1]}" )
print(f"B_A4的最大特征值为{HSA(B_A4)[0]}, 对应归一化权向量为{HSA(B_A4)[1]}" )
print(f"B_A5的最大特征值为{HSA(B_A5)[0]}, 对应归一化权向量为{HSA(B_A5)[1]}" )

上面是精确的计算。但是对于一致性较好的正反矩阵，可以近似计算最大特征值和对应特征向量的方法。这能简化运算。

近似求最大特征值和对应特征向量的方法1-和积法

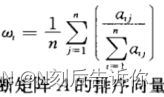
和积法的python实现

def roughHSA(mat): # 和积法：列向量的算数平均来近似特征向量，然后利用A*w=lambda*w获得最大特征值
    # 列向量归一化+算数平均
    rough_normal_q = np.average(mat/np.sum(mat, axis=0), axis=1)
    # 对应的最大特征值
    rough_max_eig = np.round(np.average(mat@rough_normal_q/rough_normal_q), 3)
    return rough_max_eig, rough_normal_q

print(f"A_Z的最大特征值为{roughHSA(A_Z)[0]}, 对应归一化权向量为{roughHSA(A_Z)[1]}" )
print(f"B_A1的最大特征值为{roughHSA(B_A1)[0]}, 对应归一化权向量为{roughHSA(B_A1)[1]}" )
print(f"B_A2的最大特征值为{roughHSA(B_A2)[0]}, 对应归一化权向量为{roughHSA(B_A2)[1]}" )
print(f"B_A3的最大特征值为{roughHSA(B_A3)[0]}, 对应归一化权向量为{roughHSA(B_A3)[1]}" )
print(f"B_A4的最大特征值为{roughHSA(B_A4)[0]}, 对应归一化权向量为{roughHSA(B_A4)[1]}" )
print(f"B_A5的最大特征值为{roughHSA(B_A5)[0]}, 对应归一化权向量为{roughHSA(B_A5)[1]}" )

可以看到结果是近似的
关于和积法的理论依据可以参考：层次分析法中和积法(ANC)排序结果的理论推导

近似求最大特征值和对应特征向量的方法1-方根法(略)

计算CI、查RI、并计算CR，检验一致性是否通过

对于准则层对目标层的判断矩阵A_Z，其最大特征值为5.073，对应n=5，可以得到CR=0.016<0.1，通过一致性检验。

层次总排序及其一致性检验

层次总排序：计算某一层次所有因素对最高层(目标层)相对重要性的权重

计算权向量

层次总排序的一致性检验

代码实现

import numpy as np
# 准则层对目标层的判断矩阵
A_Z = np.array([[1, 1/2, 4, 3, 3], 
              [2, 1, 7, 5, 5],
              [1/4, 1/7, 1, 1/2, 1/3],
              [1/3, 1/5, 2, 1, 1],
              [1/3, 1/5, 3, 1, 1]])
# 方案(措施)层对准则层的判断矩阵
B_A1 = np.array([[1, 2, 5], 
              [1/2, 1, 2],
              [1/5, 1/2, 1]])
B_A2 = np.array([[1, 1/3, 1/8], 
              [3, 1, 1/3],
              [8, 3, 1]])
B_A3 = np.array([[1, 1, 3], 
              [1, 1, 3],
              [1/3, 1/3, 1]])
B_A4 = np.array([[1, 3, 4], 
              [1/3, 1, 1],
              [1/4, 1, 1]])
B_A5 = np.array([[1, 1, 1/4], 
              [1, 1, 1/4],
              [4, 4, 1]])
def roughHSA(mat): # 和积法：列向量的算数平均来近似特征向量，然后利用A*w=lambda*w获得最大特征值
    # 列向量归一化+算数平均
    rough_normal_q = np.average(mat/np.sum(mat, axis=0), axis=1)
    # 对应的最大特征值
    rough_max_eig = np.round(np.average(mat@rough_normal_q/rough_normal_q), 3)
    return rough_max_eig, rough_normal_q
    
def CI_RI(mat):
    lamb = roughHSA(mat)[0]
    n = mat.shape[0]
    CI = (lamb-n)/(n-1)
    RI = [0, 0, 0, 0.58, 0.90, 1.12, 1.24, 1.32, 1.41, 1.45, 1.49, 1.51]
    return CI, RI[n]

# 准则层对目标层
for mat in ['A_Z']:
    print(f"{mat}的最大特征值为{roughHSA(eval(mat))[0]}, 对应归一化权向量为{roughHSA(eval(mat))[1]}" )
    A = roughHSA(eval(mat))[1]
    CI, RI = CI_RI(eval(mat))
    if CI/RI<0.1:
        print('层次单排序通过一致性检验')
    else:
        print('层次单排序未通过一致性检验')

# # 方案(措施)层对准则层
B = []
CI_list = []
RI_list = []
for mat in ['B_A1', 'B_A2', 'B_A3', 'B_A4', 'B_A5']:
    print(f"{mat}的最大特征值为{roughHSA(eval(mat))[0]}, 对应归一化权向量为{roughHSA(eval(mat))[1]}" )
    B.append(roughHSA(eval(mat))[1])
    CI, RI = CI_RI(eval(mat))
    CI_list.append(CI)
    RI_list.append(RI)
    if CI/RI<0.1:
        print('层次单排序通过一致性检验')
    else:
        print('层次单排序未通过一致性检验')

B=np.array(B)
print("B层的层次总排序为", B.T@A)

B层的层次总排序为 [0.29900738 0.24541338 0.45557924]
所以选方案3。