文章目录
- 1.Overview
- 2.CNF 3-sat
- 3. Gadgets
- 3.1 Concolorous Edges
- 3.2 Starter/Variable Gadget
- 3.3 Splitter Gadget
- 3.4 OR Gadget
- 3.5 Clause Gadget
- 4. To Planar Graph
最近在学 6.890,然后 devans 刚好问了我这个问题,然后尝试编了一个证明。
1.Overview
我们从 CNF 3-sat 问题规约到 3-染色问题(G3C),随后从 3-染色问题可以轻松的规约到
k
k
k-染色问题
k
≥
3
k\geq 3
k≥3。
首先我们引入同色边的概念,利用同色边我们可以方便的确定三种颜色中的一种,通过一个三元环确定三个颜色分别对应 T/F/O,随后利用 variable gadget 确定每一个 3-sat 变量的取值,对于每一个 clause gadget 输出的结果即三个输入的或,利用 OR gadget 实现,要求每一个 clause 的返回结果均为 true。这样构建出来的一个图我们声称,如果这个图有 3-染色,则原来的 3-sat 问题有解,即得到
C
N
F
3
S
A
T
≤
p
G
3
C
CNF3SAT\leq_p G3C
CNF3SAT≤pG3C,而接下来的
G
3
C
≤
p
G
C
G3C\leq_pGC
G3C≤pGC 是比较显然的。
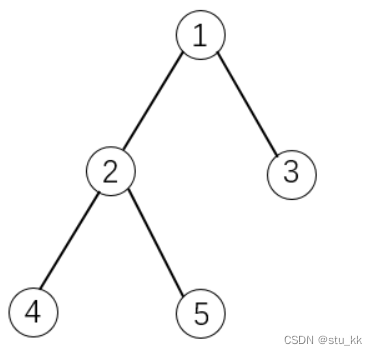
最后构建的图
G
G
G 形如下图:

2.CNF 3-sat
CNF 3-sat 问题是指,给布尔变量 x 1 , x 2 , ⋯ x_1,x_2,\cdots x1,x2,⋯ 赋值,是的一个布尔表达式的值为真,其中这个布尔表达式形如若干个 clause 的与,其中一个 clause 为三个变量(可能带非运算符)的或的形式。下面是一个可能的 CNT 布尔表达式
F = ( x 1 ∨ ¬ x 2 ∨ x 3 ) ∧ ( x 1 ∨ x 2 ∨ ¬ x 4 ) ∧ ( x 1 ∨ ¬ x 2 ∨ ¬ x 3 ) F=(x_1\vee \neg x_2\vee x_3)\wedge(x_1\vee x_2 \vee \neg x_4)\wedge (x_1 \vee \neg x_2 \vee \neg x_3) F=(x1∨¬x2∨x3)∧(x1∨x2∨¬x4)∧(x1∨¬x2∨¬x3)
3. Gadgets
3.1 Concolorous Edges
我们把下面这个子图称之为一条同色边,用一条红色的边来表示,不难发现,A 和 B 两个点的染色必须相同。

3.2 Starter/Variable Gadget
我们首先需要给每个变量确定他的取值,而我们有三个颜色,一种自然的方法就是设定一种颜色代表他为 T,一种为 F,剩下的一种叫做 O
为了实现这件事情,我们先用一个三元环作为 starter gadget,通过这个三元环的染色方法,可以确定 TFO 对应的是哪一种颜色,然后对于变量再设立一个三元环,其中一个点用同色边钦定其为 O,剩下两个分别代表
x
i
x_i
xi 和
x
i
ˉ
\bar{x_i}
xiˉ,若代表
x
i
x_i
xi 的点选择的颜色 T,则
x
i
x_i
xi 取值为 True,否则取值为 False。

3.3 Splitter Gadget
显然分裂一个状态是好做的,我们只需要直接用红边进行分叉即可
3.4 OR Gadget
我们这里需要定义一个 OR gadget,根据两个输入的节点的颜色,定义输出节点的颜色。
直接设计是较为困难的,我们考虑构造一个 gadget 满足一个较为弱化的条件,当两个输入为 F,F 的时候,一定输出 F
一个直观的设计师这样的:

A,B 为输入,E 为输出
而在输入为 T,F 的时候,输出可以为 T/F 中的任意一个,注意和 starter 里面的 O 节点连边后实际上保证了输出不为 O。
下面我们会证明,如果此时取 F 的话对于答案一定是不优的。
3.5 Clause Gadget
这里我们要求三个输入中的一个至少一个为真,只需要把 A,B OR 起来的结果再和 C OR 一下即可,最后设计出来的如图:

其中 OR1 和 OR2 分别是 OR gadget
因为我们要求每一个 clause 为 True,所以我们向 OR2 的 输出端 连上 F 和 O 相当于钦定输出必须为 True,这也就意味着在 OR1 和 OR2 的输入中,T,F 的情况下返回 F 一定是不优的。
把上面这些 gadgets 拼一起,就得到了第一节里面的总流程的模式图。
4. To Planar Graph
很遗憾的是,上面这个做法很难拓展到平面图三染色问题,因为这个 Crossover Gadget 很难设计。至少我还不会
但是根据 stackexchange 上面的一篇回答平面图三染色同样也是 NPC 的。
因此这个做法的推广的瓶颈在于如何把两条相交的红边转化成等价的平面图。
或许过两天想出来了来填坑。