leetcode 236. 二叉树的最近公共祖先

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

示例 1：

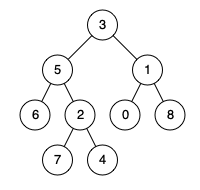
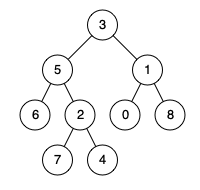
输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出：3
解释：节点 5 和节点 1 的最近公共祖先是节点3 。

示例 2：

 

输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出：5
解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

示例 3：

输入：root = [1,2], p = 1, q = 2
输出：1

 代码

//leetcode 236. 二叉树的最近公共祖先
// 回溯
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		if (root == nullptr || root == p || root == q)
		{
			return root;
		}
		TreeNode* left = lowestCommonAncestor(root->left, p, q);
		TreeNode* right = lowestCommonAncestor(root->right, p, q);
		if (left != nullptr && right != nullptr)
		{
			return root;
		}
		return left ? left : right;
	}
};

leetcode 235. 二叉搜索树的最近公共祖先

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树:  root = [6,2,8,0,4,7,9,null,null,3,5]

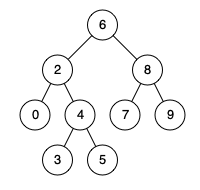
示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6 
解释: 节点 2 和节点 8 的最近公共祖先是 6。

示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2和节点 4的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

 

 代码

// leetcode 235. 二叉搜索树的最近公共祖先
// 层序遍历第一个在pq之间的结点
class Solution {
public:
	TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
		int a = min(p->val, q->val);
		int b = max(p->val, q->val);

		queue<TreeNode*> que;
		que.push(root);

		while (!que.empty())
		{
			TreeNode* cur = que.front();
			que.pop();
			if (cur->val >= a && cur->val <= b)
				return cur;

			if (cur->left)
				que.push(cur->left);
			if (cur->right)
				que.push(cur->right);
		}
		return NULL;
	}
};