题目

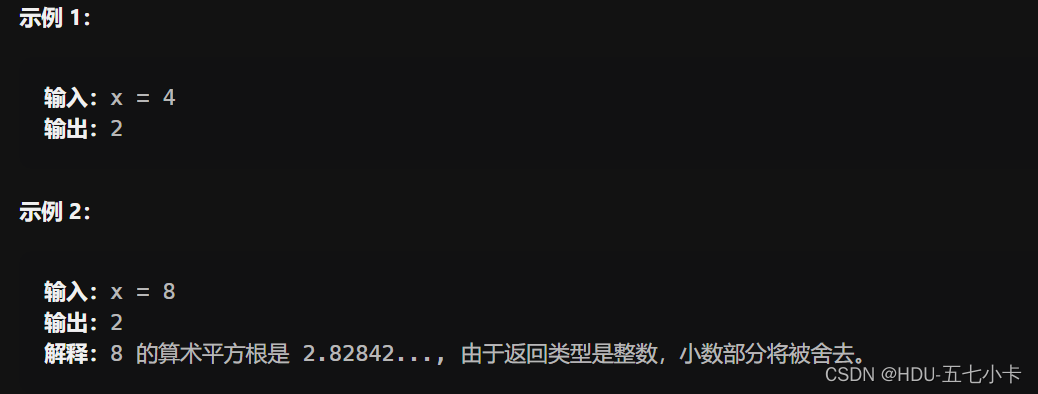
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

思路

二分查找：

因为题目中说了，结果只保留整数的部分，小数部分将被舍去

即：问题的答案，平方以后一定不会严格大于输入的整数，如8的平方根实际上是 2.82842，题目要求将小数部分舍去，因此输出 2，如果返回3，则3^2 = 9 > 8就不对了

这其实是一个查找整数的问题，并且这个整数是有范围的

（1）如果这个整数的平方 恰好等于 输入整数，那么就找到了这个整数
（2）如果这个整数的平方 严格大于 输入整数，那么这个整数肯定不是要找的那个数，大了就往小的猜
（3）如果这个整数的平方 严格小于 输入整数，那么这个整数 可能 是要找的那个数

另外一个整数的平方根肯定不会超过(<=)它自己的一半，但是 0 和 1 除外，因此可以在 1 到输入整数除以 2 这个范围里查找要找的平方根整数，0单独判断一下即可

class Solution {
    public int mySqrt(int x) {
        // 特殊值判断
        if (x == 0) {
            return 0;
        }
        if (x == 1) {
            return 1;
        }
        int left = 1;
        int right = x / 2;
        while (left < right) {
            int mid = left + (right - left + 1)  / 2;//有特殊测试用例，这里mid不加1会死循环
            // 注意：这里为了避免乘法溢出，改用除法
            if (mid > x / mid) {
                // 下一轮搜索区间是 [left..mid - 1],因为大于x一定不对，不用再取mid了
                right = mid - 1;
            } else {
                // 下一轮搜索区间是 [mid..right]，保证和上一个区间连起来是一个完整区间
                left = mid;//如果是小于x，mid仍然可能是答案，所以要算上
            }
        }
        return left;
    }
}