1. 题目介绍（56. 数组中数字出现的次数）

面试题56.：数组中数字出现的次数， 一共分为两小题：

• 题目一：数组中只出现一次的两个数字
• 题目二：数组中唯一只出现一次的数字

2. 题目1：数组中只出现一次的两个数字

题目链接：https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-lcof/

2.1 题目介绍

一个整型数组 nums 里除两个数字之外，其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是 O(n)，空间复杂度是 O(1)

【测试用例】：
示例1：

输入：nums = [4,1,4,6]
输出：[1,6] 或 [6,1]

示例2：

输入：nums = [1,2,10,4,1,4,3,3]
输出：[2,10] 或 [10,2]

【条件约束】：

限制：

• 2 <= nums.length <= 10000

2.2 题解 – 位运算（XOR）-- O(n)

时间复杂度O(n)，空间复杂度O(1)

【解题思路】：
该问题是问在一个数组中找出 两个只出现一次的数字 ，那么我们可以先从这个数组中 只有一个数字只出现了一次 开始考虑：

• 首先我们可以想到 异或运算 的一个性质：任何一个数字异或它自己都等于0；也就是说，如果我们从头到尾依次异或数组中的每个数字，那么最终的结果刚好是那个只出现依次的数组，因为那些成对出现两次的数字全部在异或中抵消了（当然，这也是一个前提条件，要求 数组中的其它数字都是出现了两次，而不是三次或其他次，只能是 偶数次 才行）

……
既然，我们有了得到只出现一次数字的办法，那么我们就要想怎么求出两个只出现一次的数字：

• 我们可以试着将 原数组分成两个子数组 ，使得每个子数组包含一个只出现一次的数字，而其它数字都承兑出现两次。只要能够这样拆分成两个数组，那么我们就可以按照前面的办法分别找出两个只出现一次的数字

……
【实现策略】：

1. 首先还是先进行无效输入的判断，判断数组长度 nums.length 是否小于等于 0，如果是，则说明是无效数据；
2. 定义变量 exclusiveOr，获取数组中所有元素的异或结果（该结果可以等同于 数组中两个唯一只出现一次的数字 的异或结果）；
3. 我们可以根据这个异或结果（exclusiveOr），去寻找这两个数字是在哪一位开始不同的，即从低位到高位，第一个 Bit为1 的位置；
4. 找到这个位置后，我们就可以根据这个位置进行分组了，我们将 该位为1 的数据分为一组，不为1 的分为一组，然后对其进行异或，最后剩下的数字就是我们要找到的两个数字了。

class Solution {
    // Solution1：异或分组和筛选
    public int[] singleNumbers(int[] nums) {
        // 无效输入判断
        if (nums.length <= 0) return null;
        // 将数组中所有元素进行异或
        int exclusiveOr = 0;
        for (int i = 0; i< nums.length; i++) {
            // 异或完成后，一样的会被抵消，只剩下不一样的两个数字，需要我们对其进行分组
            exclusiveOr ^= nums[i];
        }
        int indexBitIs1 = findFirstBitIs1(exclusiveOr);
        // 遍历数组并分组判断
        int[] res = new int[2];
        for (int j = 0; j < nums.length; j++) {
            if (isBit1(nums[j], indexBitIs1)) res[0] ^= nums[j];
            else res[1] ^= nums[j];
        }
        // 循环结束，返回结果
        return res;

    }
    // 从右向左寻找第一位为1的位数
    public int findFirstBitIs1(int num) {
        int indexFirstBitIs1 = 0;
        while ((num & 1) == 0 && (indexFirstBitIs1 < 32)) {
            num = num >> 1;
            indexFirstBitIs1++;
        }
        return indexFirstBitIs1;
    }
    // 判断输入的数字的indexBitIs1位是不是1
    public boolean isBit1(int num, int indexBitIs1) {
        num = num >> indexBitIs1;
        return (num & 1) != 0 ;
    }
}

代码简化：

class Solution {
    public int[] singleNumbers(int[] nums) {
        int x = 0, y = 0, n = 0, m = 1;
        for(int num : nums)               // 1. 遍历异或
            n ^= num;
        while((n & m) == 0)               // 2. 循环左移，计算 m
            m <<= 1;
        for(int num: nums) {              // 3. 遍历 nums 分组
            if((num & m) != 0) x ^= num;  // 4. 当 num & m != 0
            else y ^= num;                // 4. 当 num & m == 0
        }
        return new int[] {x, y};          // 5. 返回出现一次的数字
    }
}

3. 题目2：

题目链接：https://leetcode.cn/problems/shu-zu-zhong-shu-zi-chu-xian-de-ci-shu-ii-lcof/

3.1 题目介绍

在一个数组 nums 中除一个数字只出现一次之外，其他数字都出现了三次。请找出那个只出现一次的数字。

【测试用例】：
示例1：

输入：nums = [3,4,3,3]
输出：4

示例2：

输入：nums = [9,1,7,9,7,9,7]
输出：1

【条件约束】：

限制：

• 1 <= nums.length <= 10000
• 1 <= nums[i] < 2^31

3.2 题解 – 位运算 – O(n)

时间复杂度O(n)，空间复杂度O(1)

【解题思路】：
因为三个相同的数字的异或结果还是该数字，因此我们在这里就不能再使用异或运算解决该问题了，不过我们还是可以沿用位运算的思路：

1. 如果一个数字出现三次，那么它的二进制表示的每一位（0 或者 1）也出现三次；
2. 如果把所有出现三次的数字的二进制表示的每一位都分别加起来，那么每一位的和都能被 3 整除；
3. 我们把数组中所有数字的二进制表示的每一位都加起来，如果某一位的和能被 3 整除，那么那个只出现一次的数字二进制表示中对应的那一位是 0；否则就是 1.

……
这种解法的时间效率是 O(n)，我们需要一个长度为 32 的辅助数组存储二进制表示的每一位的和。当然，除此之外，还有其它解法：

1. 从排序数组中找到只出现一次的数字，但排序需要额外的 O(nlogn) 的时间；
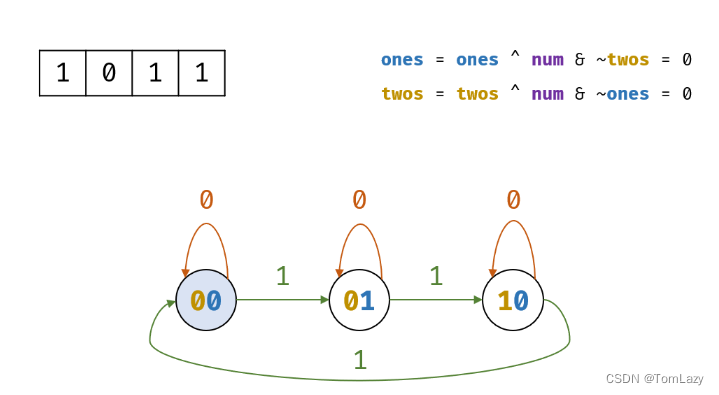
2. 用一个哈希表来记录数组中每个数字出现的次数，但这个哈希表需要额外的 O(n) 的空间；
3. 有限状态自动机：各二进制位的 位运算规则相同 ，因此只需考虑一位即可。如下图所示，对于所有数字中的某二进制位 1 的个数，存在 3 种状态，即对 3 余数为 0,1,2 ；该方法虽然效率较高，但也较难理解

class Solution {
    // Solution1：位运算
    public int singleNumber(int[] nums) {
        // 定义辅助数组 counts，用来存储二进制表示的每一位的和
        int[] counts = new int[32];
        // 循环遍历数组中的所有数
        for(int num : nums) {
            // 将该数的32位分别存入数组
            for(int j = 0; j < 32; j++) {
                counts[j] += num & 1;
                num = num >> 1;
            }
        }
        int res = 0, m = 3;
        for(int i = 0; i < 32; i++) {
            // 移位处理
            res <<= 1;
            // 如果 某一位的和能被 3 整除，那么那个只出现一次的数字
            // 二进制表示中对应的哪一位是0；否则就是1
            res |= counts[31 - i] % m;
        }
        return res;
    }
}

有限状态自动机：

class Solution {
    public int singleNumber(int[] nums) {
        int ones = 0, twos = 0;
        for(int num : nums){
            ones = ones ^ num & ~twos;
            twos = twos ^ num & ~ones;
        }
        return ones;
    }
}

4. 参考资料

[1] 剑指 Offer 56 - I. 数组中数字出现的次数（位运算，清晰图解）