形式语言与自动机总结---上下文无关文法(CFG)

news2025/11/1 6:52:19

第5章上下文无关文法:

设计文法:

做题的时候发现了一个正则表达式到文法的算法 R规则

根据正则式推导右线性文法_右线性文法表达ab*_Pluto °的博客-CSDN博客

举例

设计文法的关键在于理解递归性,文法是一个迭代器

1.The set { $a^{i}b^{j}c^{k}$ | i ≠ j or j ≠ k}, that is, the set of strings of a's followed by b's followed by c's, such that there are either a different number of a's and b's or a different number of b's and c's, or both.

上方的做法是错误的做法因为没有考虑i=j=k的情况。

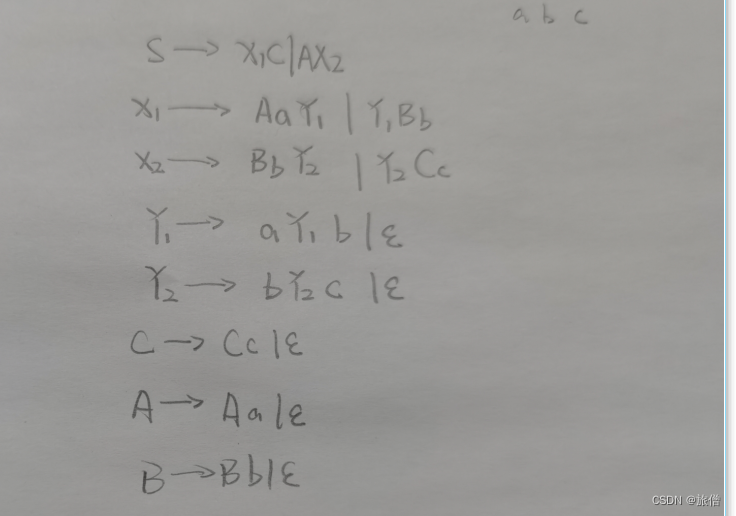
修改之后的结果

2.The set { $a^{i}b^{j}c^{k}$ |i=j|j=k} is generated by G = ( { S , T , U , A , C } , { a , b , c } , P , S )) with production P:

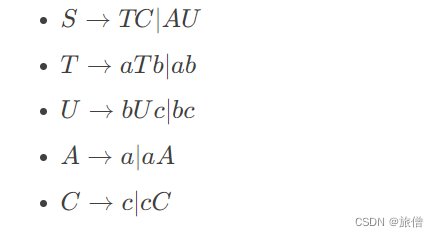
3.请为语言L = { $0^{n}1^{m} m\neq n$ }设计文法

4.设计0、1构成的串的文法，0 1数量不相等.

$S\rightarrow X_{1}|X_{2}$
$E\rightarrow1E0E|E0E1E|\varepsilon$
$X_{1}\rightarrow Y_{1}X_{1} | Y_{1}$
$Y_1\rightarrow E1E$
$Y_2\rightarrow E0E$

5. The set of all strings 0’s and 1’s that are not of the form ww, that is , not equal to any string repeated.

$S\rightarrow A|B|AB|BA$
$A\rightarrow CAC|a$
$B\rightarrow CBC|b$
$C\rightarrow a|b$

6.The set of all strings with twice as many 0's as 1's.

$S\rightarrow S0S0S1S|S0S1S0S|S1S0S0S|\varepsilon$

7.设计 Lj≥2i = { $a^{i}b^{j}$ | j ≥ 2i} 的文法.

S→AB
A→aAbb I 空串
B→Bb I 空串

8. L= { $0^{n}1^{n}$ | n $\geq$ 0 and n $\neq$ 3}

$S\rightarrow \varepsilon |01|0011|0000A1111$
$A\rightarrow 0A1|\varepsilon$

9.L(0 0* 11* 22* 00* 11* 22* 00* 11* 22*) Hint : The language defined by the regular expression.

分析:看起来像是012202012然后每一个的子字符可以重复, $(00^{*}11^{*}22^{*})^{3}$

$S\rightarrow AAA$ 相当于三次方
$A\rightarrow 0A_{1}1B2C$
$A_1\rightarrow 0A_{1}|\varepsilon$
$B\rightarrow 1B|\varepsilon$
$C\rightarrow 2C|\varepsilon$

10. L = { $a^{i}b^{j}|i\neq jand i\neq 2j$ |}

explaination:分成两种情况： $i\neq j \, \, and \,\, i \neq 2j$

$\Rightarrow i<j\, \, |\, \, j<i<2j\, \, |i>2j$

$S\rightarrow X_{1}|X_{2}|X_{3}$

11.L ={ ${a^{i}b^{j}c^{k}|i+j\neq k}$ }

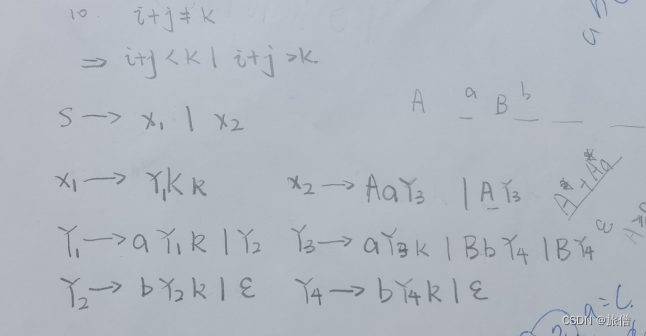
验证某个串是否在文法中:派生使用树来判断字符串是否在文法中

12.构造右线性文法:

(1) $S\rightarrow AB|BA$

$A\rightarrow aA|\varepsilon$ $B\rightarrow bB | \varepsilon$

(2) $S\rightarrow aS\, \, |\,\,bS\,\,|abb$

(3) $S\rightarrow bA \,\,\,\,\,\,\, A\rightarrow aA|a$

(4) 正则语言是(a+b)*(aa+bb)*(a+b)* 所以根据R规则

$S\rightarrow (a+b)S\,\,|\,\,bbA\,\,|\,\,aaA$

$A\rightarrow (a+b)A\,\,| \varepsilon$ $A\rightarrow (a+b)A|\varepsilon$

13. Design CFG for strings in {0,1} * in which the number of 0s is greater than or equal to the number of 1s.

$S\rightarrow 0S1|1S0|SS|0S|\varepsilon$

14.Design CFG for L = {w ∈ {(, )} ∗ | w is a string of balanced parentheses}.(括号匹配)

$S\rightarrow \,S(S)S|\varepsilon$

$S\rightarrow (S)|SS|\varepsilon$

15.L ={ $a^{i}b^{j}c^{k}(i+j=k)$ } 感觉构造PDA然后转换比较简单

$S\rightarrow aDc|\varepsilon$

$D\rightarrow aDb|\varepsilon$

16 L ={ $a^{i}b^{j}c^{k}(j=2(i+k))$ }的CFG

$S\rightarrow AB$

$A\rightarrow aBbb|\varepsilon$

$B\rightarrow bbBc|\varepsilon$

17.L={ $a^{i}b^{j}c^{k}(k=i+j)$ } 的CFG

$S\rightarrow aDc$

$D\rightarrow bDc|\varepsilon$

文法的歧义性

1.判断一个语言具有歧义性，画出两种树

2.让你消除歧义性：重新设计文法。

文法的化简

消除无用的符号

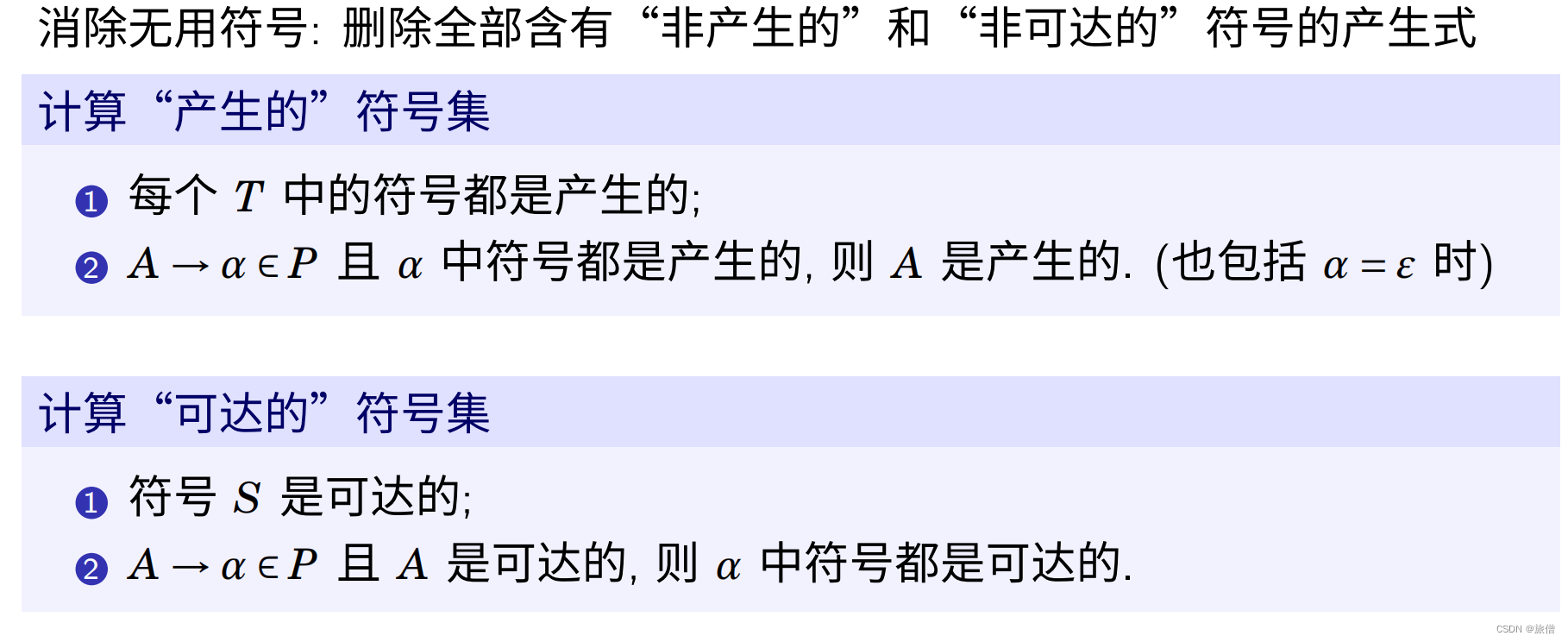
一定要注意顺序

先消除产生的
再消除可达的
否则消除不干净

先消除非产生的 $S\rightarrow a$ $A\rightarrow b$

再消除非可达的 $S\rightarrow a$

为啥要化简:自动机不能识别空产生式,多一步生成的操作注意顺序的问题，有利于优化编译器的识别。

消除空产生式:

$S\rightarrow AB|A|B$

$A\rightarrow aA|a$

$B\rightarrow bB|b$

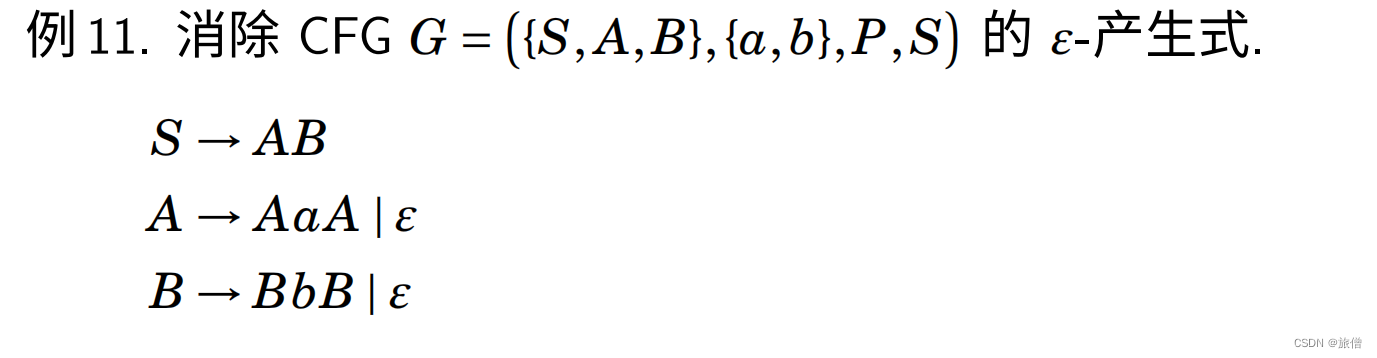
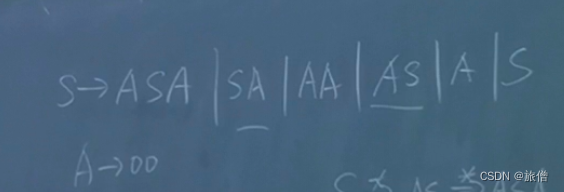
消除单元产生式

文法化简可靠顺序

消除无用符号

CNF范式

算法:

PDA转换成CFG

泵引理

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/423311.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

形式语言与自动机总结---上下文无关文法(CFG)

第5章上下文无关文法:

设计文法:

举例

文法的歧义性

文法的化简

消除空产生式:

消除单元产生式

文法化简可靠顺序

消除无用符号

CNF范式

PDA转换成CFG

泵引理

相关文章

AIGC时代，分享11款超实用AI生成内容检测工具

进程优先级

Talk预告 | ICLR‘23 斯坦福大学计算机系博士后吴泰霖：学习可控的自适应多分辨率物理仿真

灌区泵站及闸门控制自动化系统

AJAX起步入门——介绍和使用

多线程并发编程笔记07（小滴课堂）容器

ChatGPT最强对手Claude使用教程

MongoDB初认识

asp.net博客管理系统统VS开发sqlserver数据库web结构c#编程Microsoft Visual Studio

国产化ChatGPT来袭，景联文科技提供专业数据采集标注服务，人手一个专属ChatGPT或成为可能

Doris数据模型

影子账户——权限维持

MySQL的学习

Linux学习笔记——网络基础一

rc.local脚本延时启动

人工智能专题-知识表示

jenkins——环境变量、节点配置以及节点环境变量的使用

“三箭齐发”，诸葛智能三大产品全新升级，助力企业迈向数字化经营 | 爱分析调研

HTML5 ＜li＞标签、HTML5 ＜legend＞标签

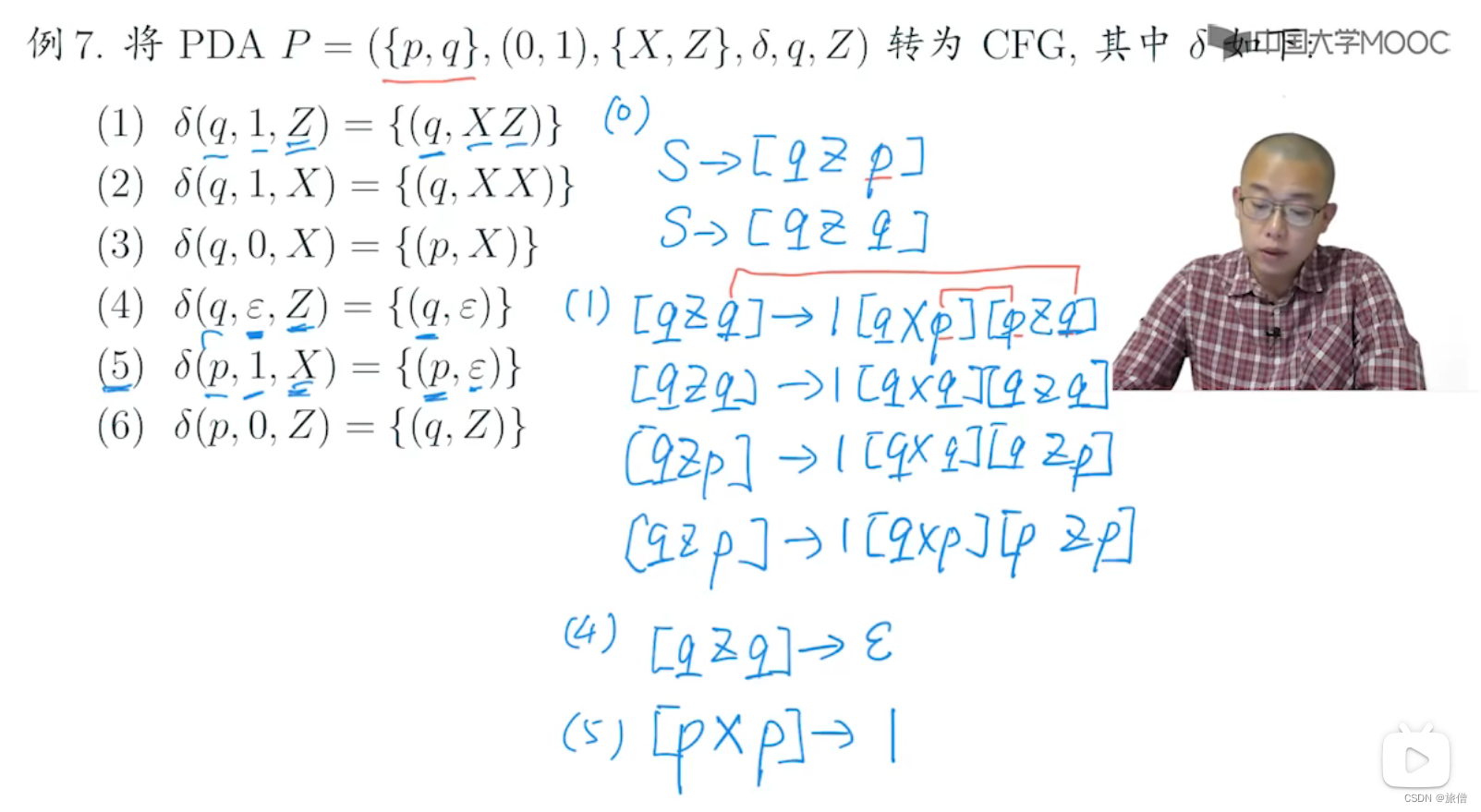
机器学习入门实例-加州房价预测-2（数据整理）