Leetcode.1631 最小体力消耗路径

news2024/11/17 3:33:46

题目链接

Leetcode.1631 最小体力消耗路径 Rating ： 1948

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns的地图 heights，其中 heights[row][col]表示格子 $(ro w, co l)$ 的高度。一开始你在最左上角的格子 $(0, 0)$ ，且你希望去最右下角的格子 $(ro w s - 1, co l u mn s - 1)$ （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的 体力值 是路径上相邻格子之间 高度差绝对值 的 最大值 决定的。

请你返回从左上角走到右下角的最小 体力消耗值 。

示例 1：

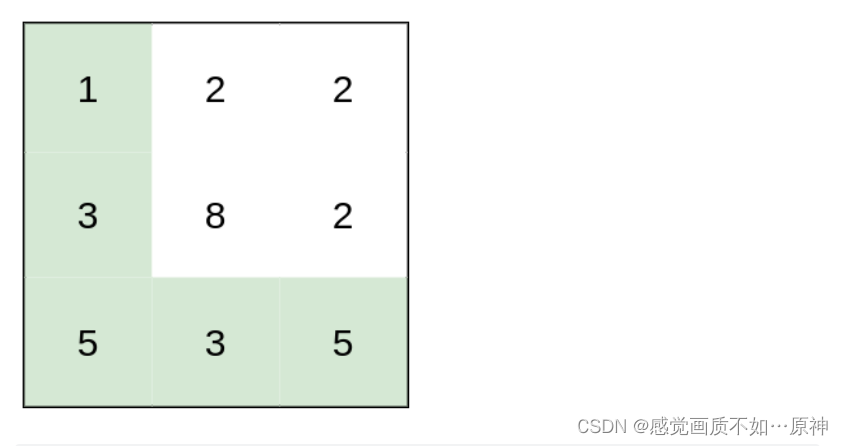
在这里插入图片描述

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

示例 2：

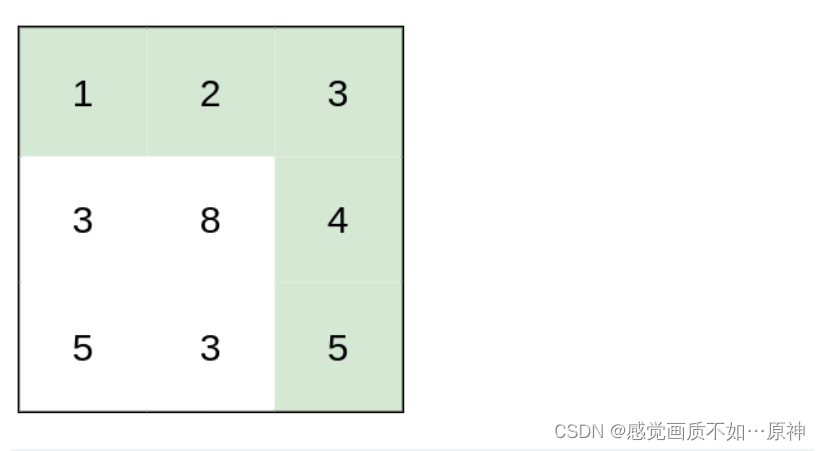
在这里插入图片描述

输入：heights = [[1,2,3],[3,8,4],[5,3,5]]
输出：1
解释：路径 [1,2,3,4,5] 的相邻格子差值绝对值最大为 1 ，比路径 [1,3,5,3,5] 更优。

示例 3：

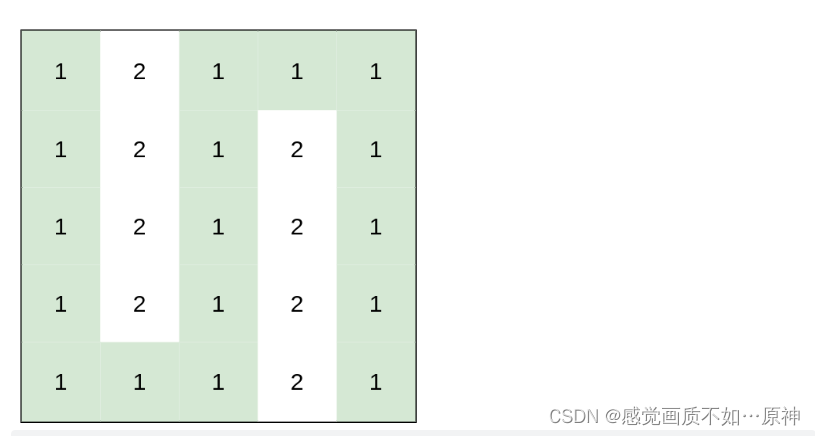
在这里插入图片描述

输入：heights = [[1,2,1,1,1],[1,2,1,2,1],[1,2,1,2,1],[1,2,1,2,1],[1,1,1,2,1]]
输出：0
解释：上图所示路径不需要消耗任何体力。

提示：

$ro w s == h e i g h t s . l e n g t h$
$co l u mn s == h e i g h t s [i] . l e n g t h$
$1 <= ro w s, co l u mn s <= 100$
$1 <= heights[i][j] <= 10^6$

解法：二分 + bfs

将原问题抽象为：

将每个格子抽象成图中的一个点；
将每两个相邻的格子之间连接一条边，长度为这两个格子本身 权值的差的绝对值 ；
原问题转化为求左上角到右下角的最短路径（路径长度为整条路径上的最大的那个权值）

我们可以二分边的权值 $mi d$ ，即 $\leq mid$ 的边才将其联通。最后我们判断从起点 $(0, 0)$ 能否到终点 $(m - 1, n - 1)$ 即可。

时间复杂度： $O (mn * l o g r)$

C++代码：


using PII = pair<int,int>;

class Solution {
    static constexpr int dir[4][2] = {{0,-1},{-1,0},{0,1},{1,0}};
public:
    int minimumEffortPath(vector<vector<int>>& g) {
        int m = g.size() , n = g[0].size();

        int l = 0 , r = 1e6;
        
        while(l < r){
            int mid = (l + r) >> 1;

            //判断位置是否被方问过了
            vector<bool> st(m * n);
            
            queue<PII> q;
            //起点入队
            q.emplace(0,0);
            st[0] = true;

            while(!q.empty()){
                auto [x,y] = q.front();
                q.pop();

                for(int i = 0;i < 4;i++){
                    int dx = x + dir[i][0] , dy = y + dir[i][1];
                    if(dx < 0 || dx >= m || dy < 0 || dy >= n) continue;
                    if(st[dx * n + dy] || abs(g[x][y] - g[dx][dy]) > mid) continue;
                    st[dx * n + dy] = true;
                    q.emplace(dx,dy);
                }
            }

            if(st[m * n - 1]) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};