文章目录

一、线段数Segment Tree
- 1.1 线段树的优势
- - 1.1.2 数组实现线段树
- 1.2 线段树结构
- - 1.2.1 创建线段树
  - 1.2.2 线段树中的区间查询
  - 1.2.3 线段树的更新
二、字典树 Trie
- 1.2 字典树结构
- - 1.2.1 创建Trie
  - 1.2.2 Trie查询
三、并查集
- 3.1 并查集的实现
- - 3.1.1 QuickFind
  - 3.1.1 QuickUnion
  - - 初始化
    - union示例

一、线段数Segment Tree

也叫区间树

1.1 线段树的优势

一面墙，长度n，每次选择一段染色
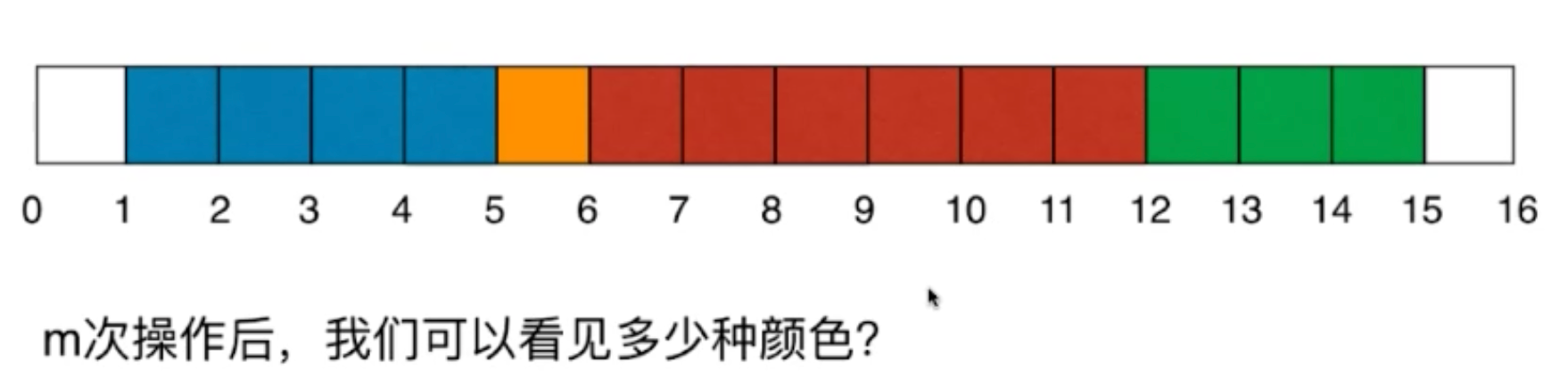
在这里插入图片描述
关注的是一个个区间

染色操作：更新区间
查询

1.1.2 数组实现线段树

可以很快想到直接用数组实现
在这里插入图片描述
数组实现时间复杂度很高，需要优化

1.2 线段树结构

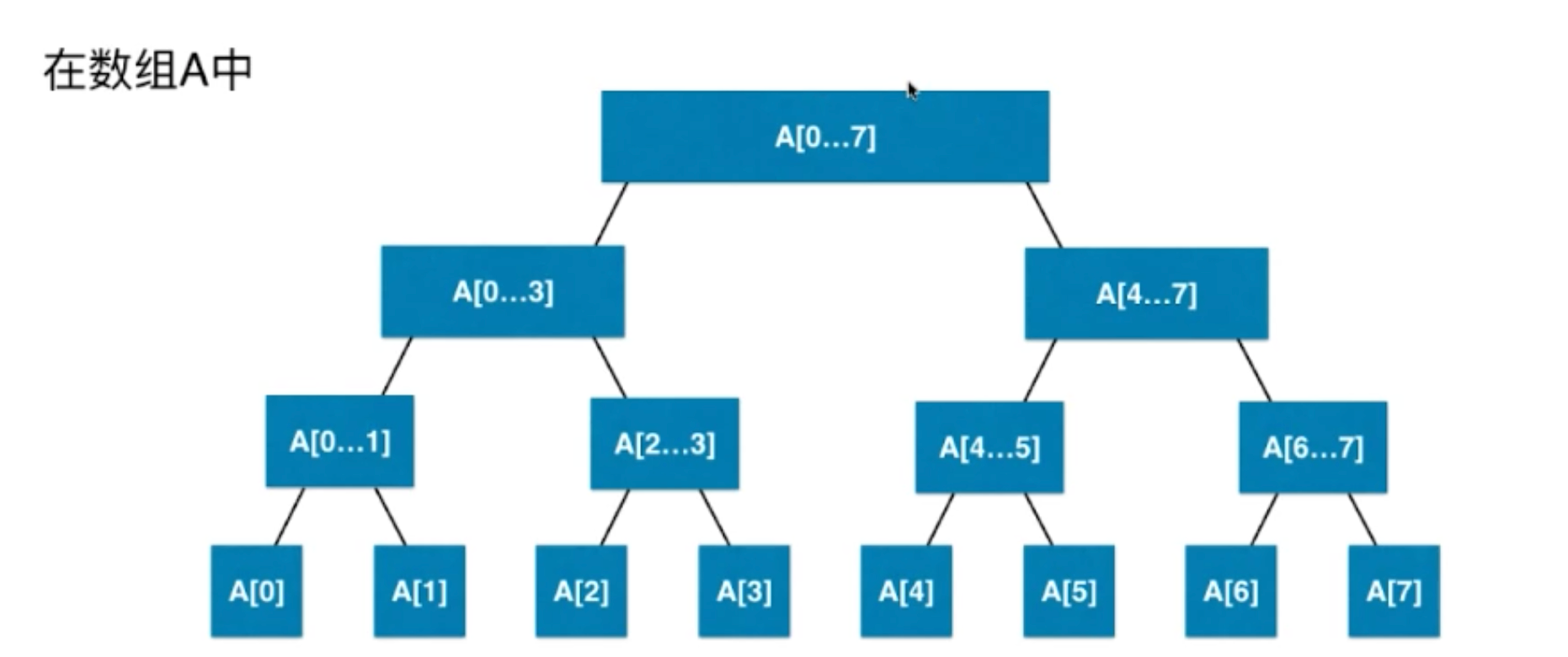
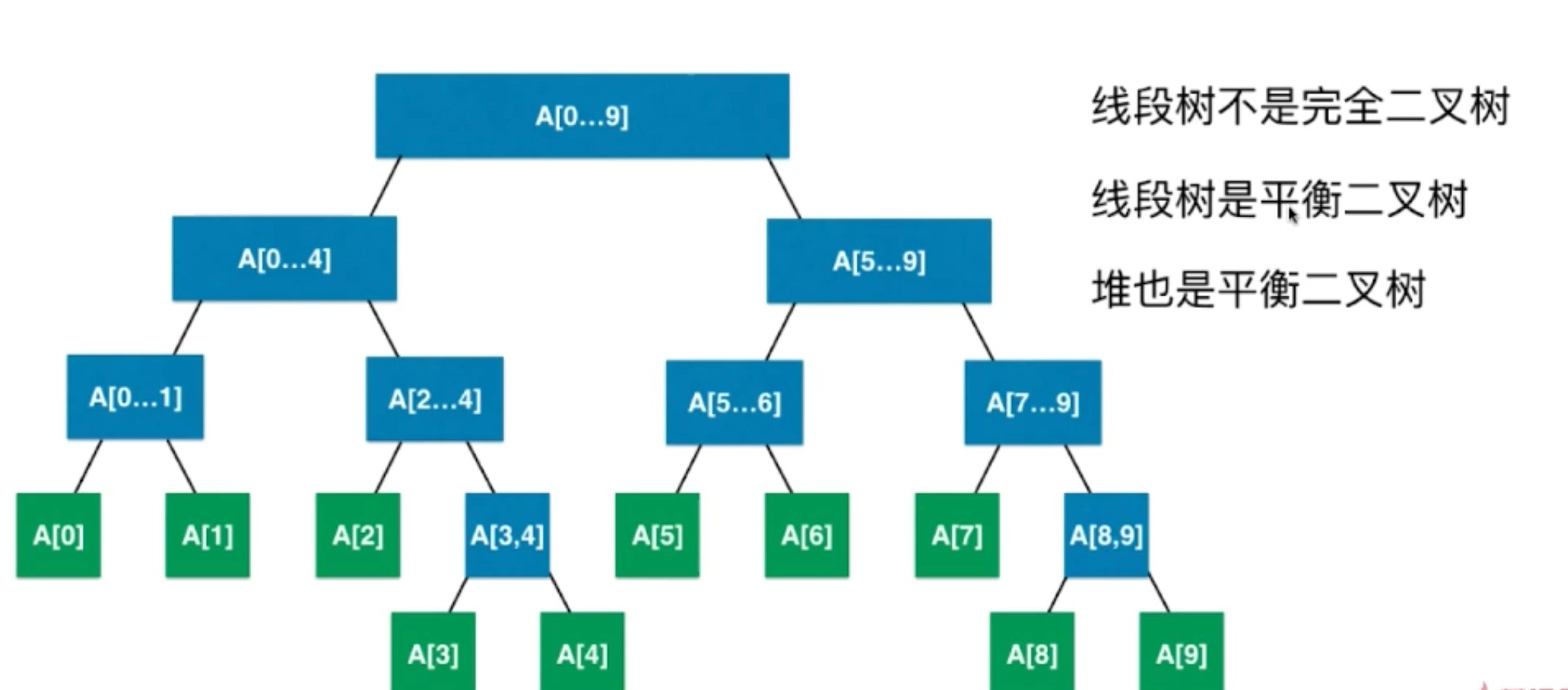
在这里插入图片描述

在这里插入图片描述
平衡二叉树：最大层 - 最小层 <= 1

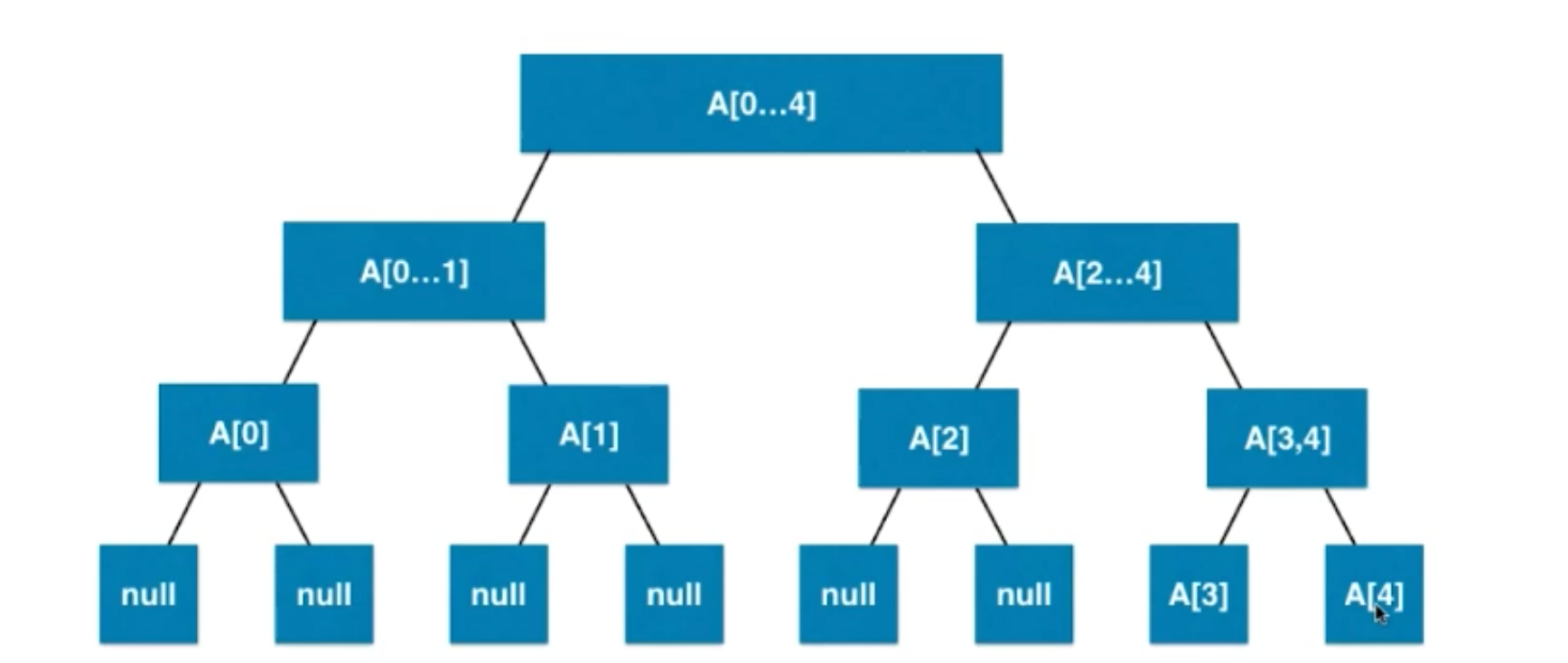
1.2.1 创建线段树

在这里插入图片描述
区间有n个元素，数组要有多少？

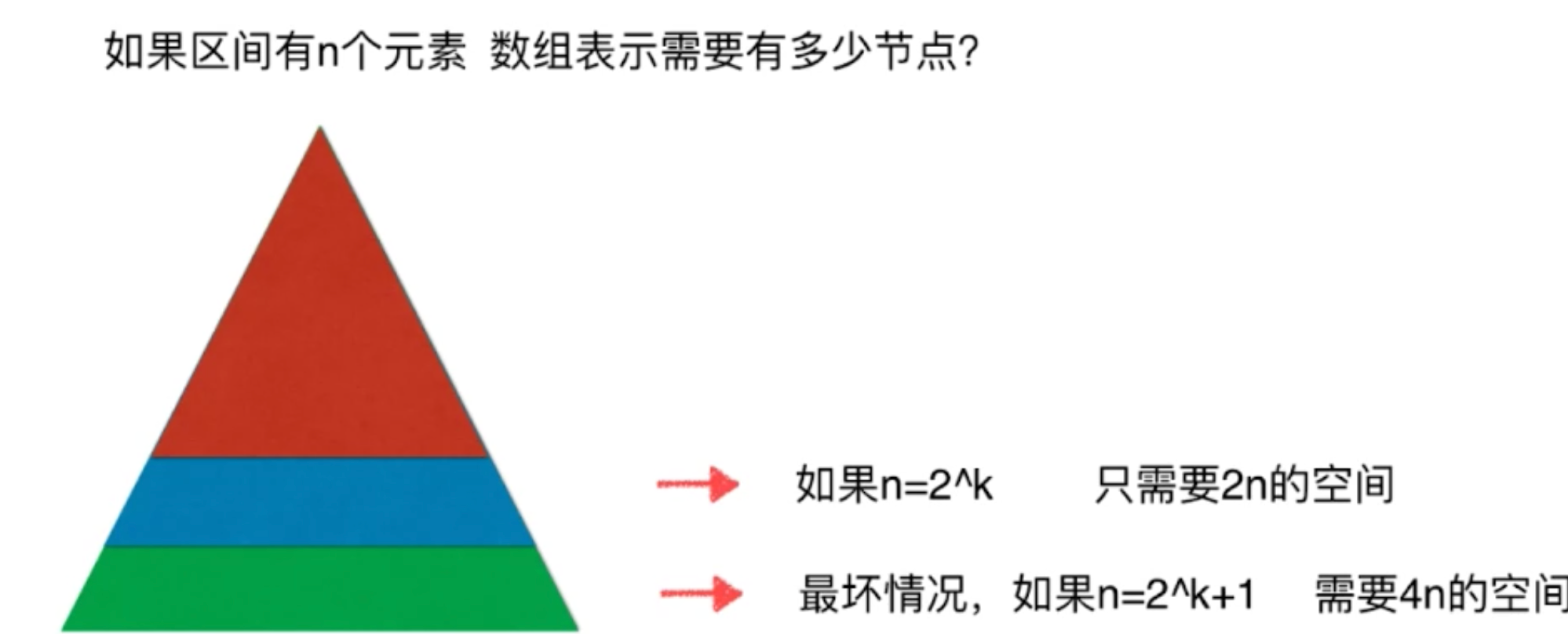
在这里插入图片描述
最差的情况4n，有接近一半的空间是浪费：

public class SegmentTree<E> {

    private E[] tree;
    private E[] data;
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger){

        this.merger = merger;

        data = (E[])new Object[arr.length];
        for(int i = 0 ; i < arr.length ; i ++)
            data[i] = arr[i];

        tree = (E[])new Object[4 * arr.length];
        buildSegmentTree(0, 0, arr.length - 1);
    }

    // 在treeIndex的位置创建表示区间[l...r]的线段树
    private void buildSegmentTree(int treeIndex, int l, int r){

        if(l == r){
            tree[treeIndex] = data[l];
            return;
        }

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);

        // int mid = (l + r) / 2;边界问题，l r 特别大 溢出
        int mid = l + (r - l) / 2;
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeIndex, mid + 1, r);

		//组合 和 业务逻辑有关
        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

    public int getSize(){
        return data.length;
    }

    public E get(int index){
        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal.");
        return data[index];
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return 2*index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return 2*index + 2;
    }

    @Override
    public String toString(){
        StringBuilder res = new StringBuilder();
        res.append('[');
        for(int i = 0 ; i < tree.length ; i ++){
            if(tree[i] != null)
                res.append(tree[i]);
            else
                res.append("null");

            if(i != tree.length - 1)
                res.append(", ");
        }
        res.append(']');
        return res.toString();
    }
}

public interface Merger<E> {
    E merge(E a, E b);
}

public class Main {

    public static void main(String[] args) {

        Integer[] nums = {-2, 0, 3, -5, 2, -1};
//        SegmentTree<Integer> segTree = new SegmentTree<>(nums,
//                new Merger<Integer>() {
//                    @Override
//                    public Integer merge(Integer a, Integer b) {
//                        return a + b;
//                    }
//                });

        SegmentTree<Integer> segTree = new SegmentTree<>(nums,
                (a, b) -> a + b);
        System.out.println(segTree);
    }
}

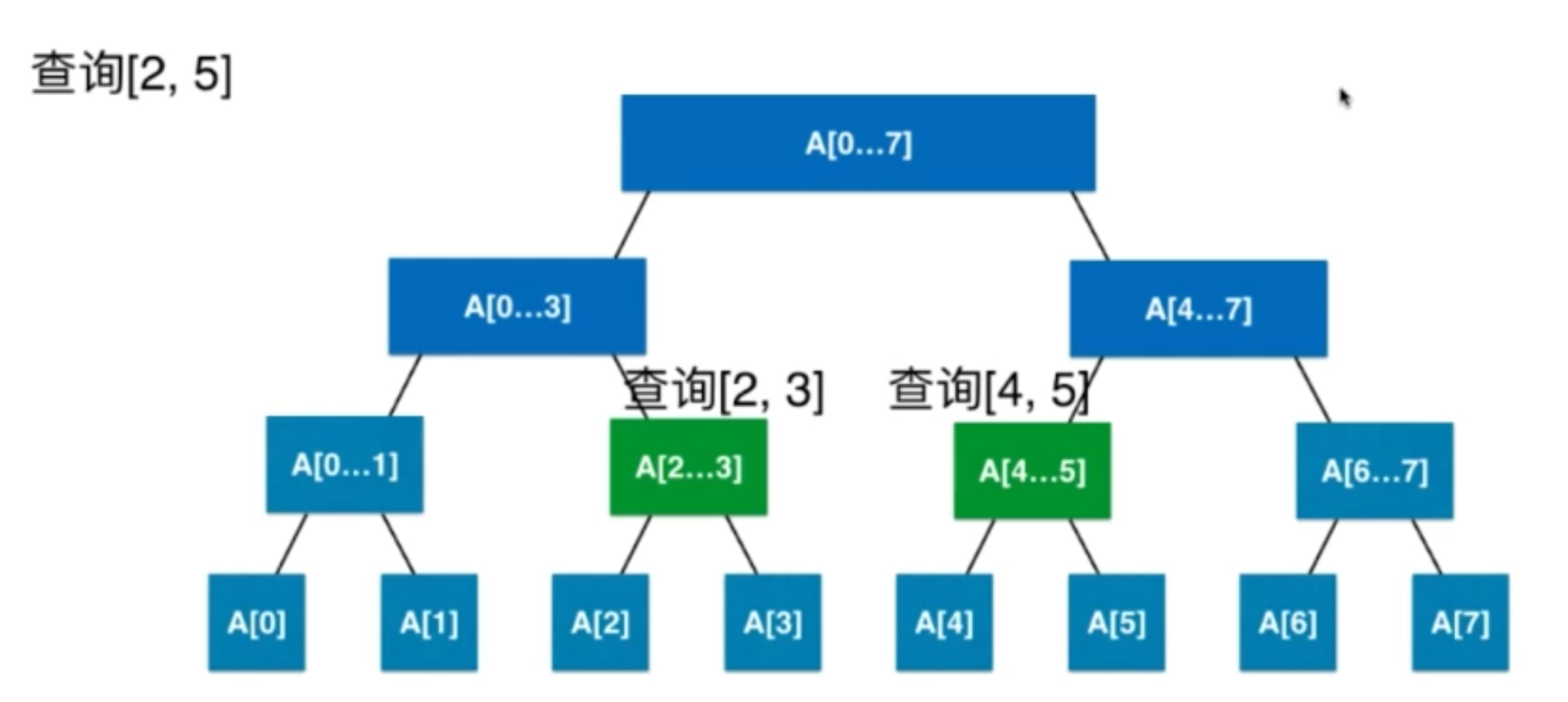
1.2.2 线段树中的区间查询

在这里插入图片描述

    public E get(int index){
        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal.");
        return data[index];
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return 2*index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return 2*index + 2;
    }

    // 返回区间[queryL, queryR]的值
    public E query(int queryL, int queryR){

        if(queryL < 0 || queryL >= data.length ||
                queryR < 0 || queryR >= data.length || queryL > queryR)
            throw new IllegalArgumentException("Index is illegal.");

        return query(0, 0, data.length - 1, queryL, queryR);
    }

    // 在以treeIndex为根的线段树中[l...r]的范围里，搜索区间[queryL...queryR]的值
    private E query(int treeIndex, int l, int r, int queryL, int queryR){

        if(l == queryL && r == queryR)
            return tree[treeIndex];

        int mid = l + (r - l) / 2;
        // treeIndex的节点分为[l...mid]和[mid+1...r]两部分

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if(queryL >= mid + 1)
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        else if(queryR <= mid)
            return query(leftTreeIndex, l, mid, queryL, queryR);

        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult, rightResult);
    }

1.2.3 线段树的更新


    // 将index位置的值，更新为e
    public void set(int index, E e){

        if(index < 0 || index >= data.length)
            throw new IllegalArgumentException("Index is illegal");

        data[index] = e;
        set(0, 0, data.length - 1, index, e);
    }

    // 在以treeIndex为根的线段树中更新index的值为e
    private void set(int treeIndex, int l, int r, int index, E e){

        if(l == r){
            tree[treeIndex] = e;
            return;
        }

        int mid = l + (r - l) / 2;
        // treeIndex的节点分为[l...mid]和[mid+1...r]两部分

        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if(index >= mid + 1)
            set(rightTreeIndex, mid + 1, r, index, e);
        else // index <= mid
            set(leftTreeIndex, l, mid, index, e);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeIndex]);
    }

二、字典树 Trie

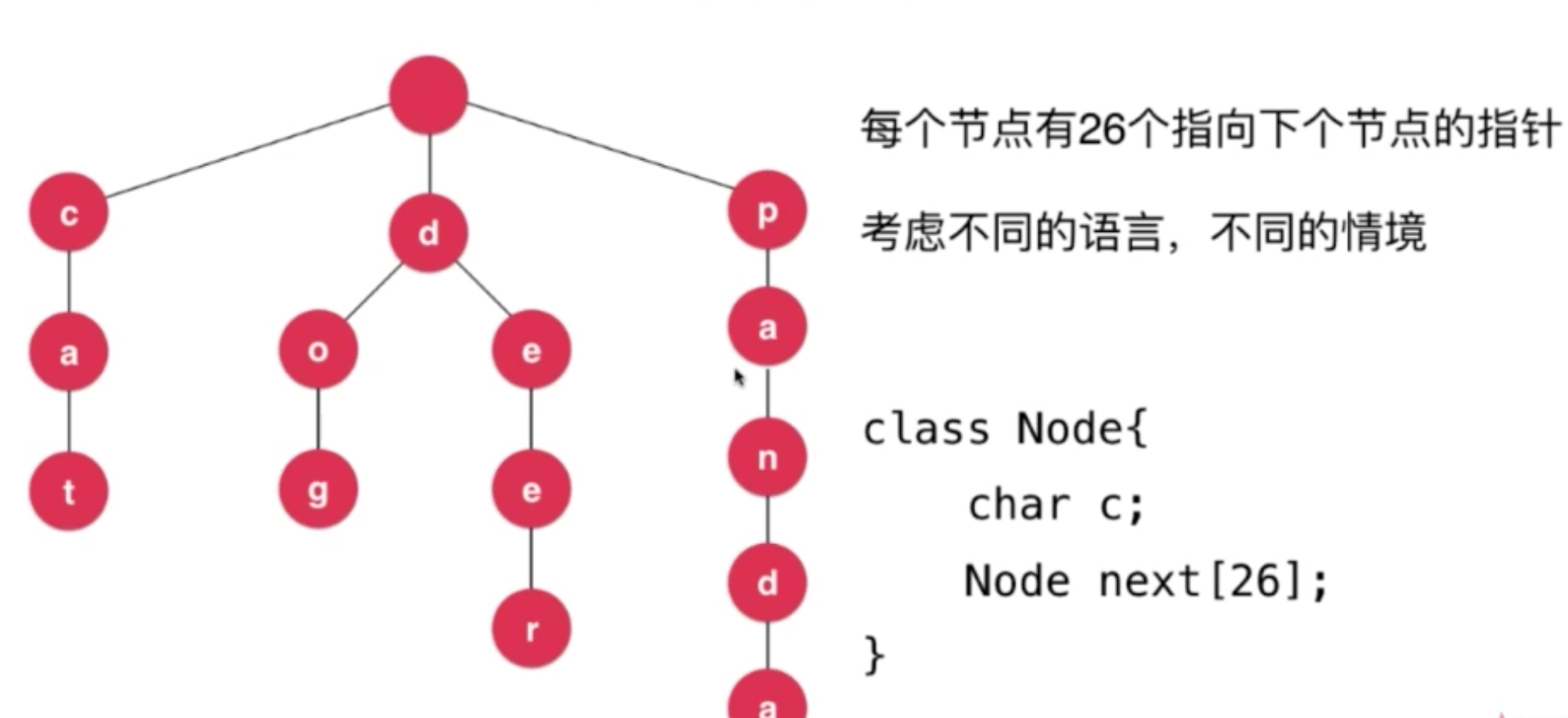
在这里插入图片描述

区分大小写、字符，可以设计的更灵活，用Map 灵活若干
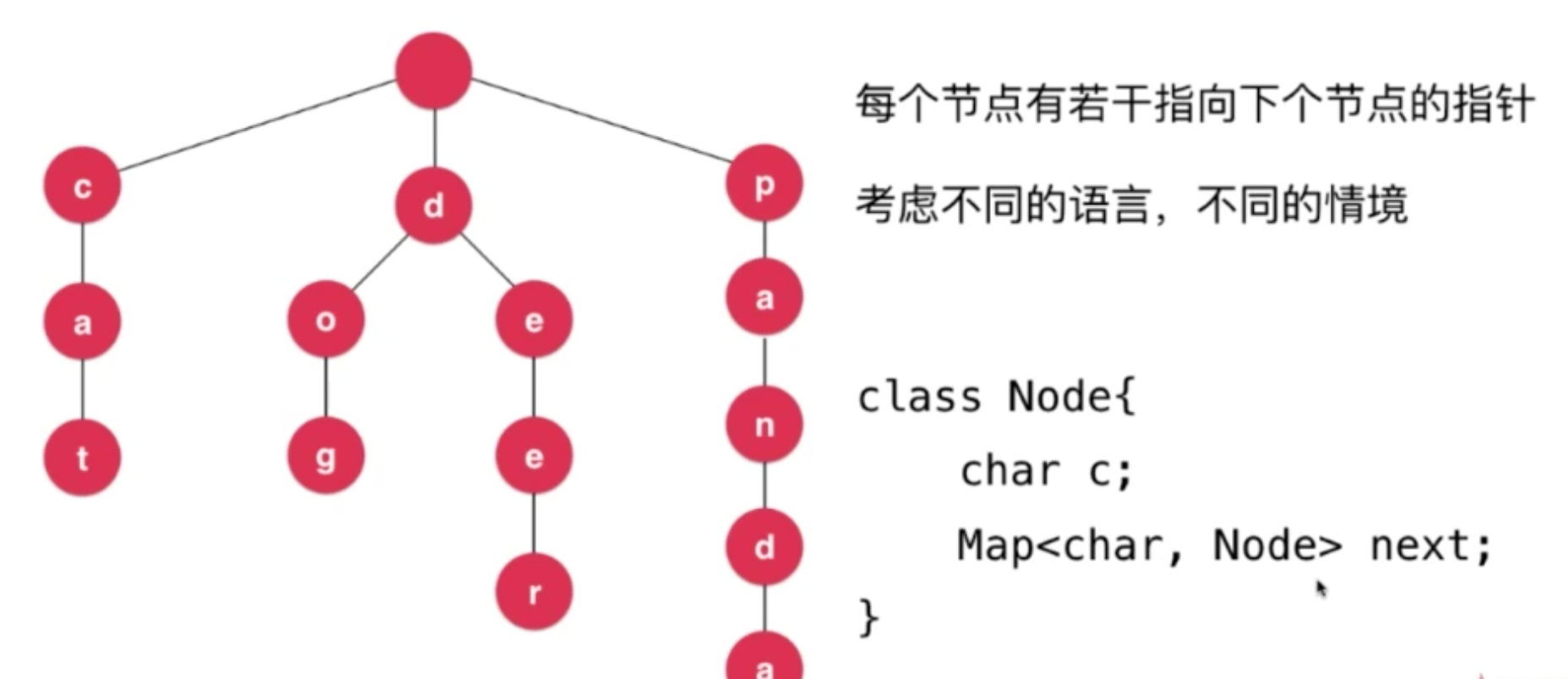
在这里插入图片描述

查找之前就已经知道节点的内容，因此可以省略char c
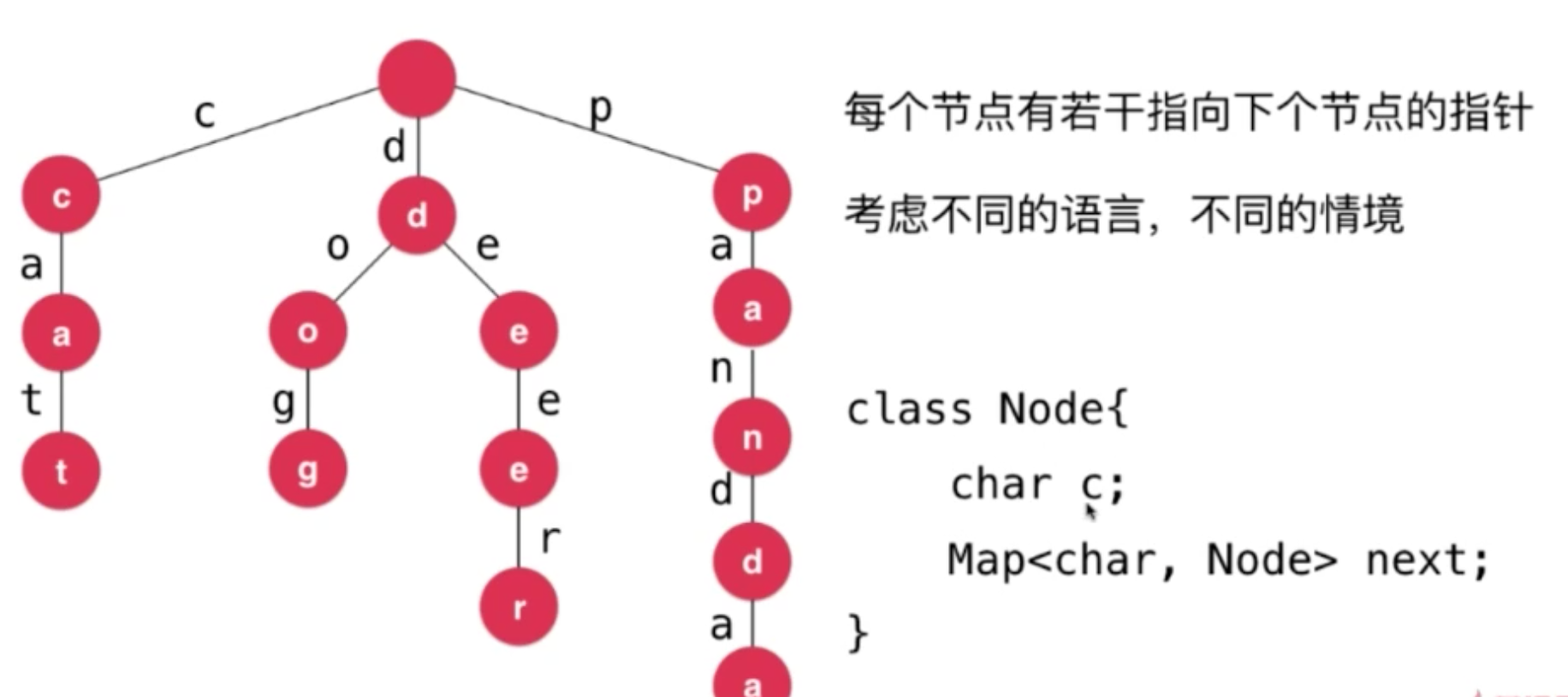
在这里插入图片描述
有一些单词中间就可能是一个单词 pan(平底锅) panda(熊猫)
因此需要指定一个标记 isWord ，来标记是否是完整的单词

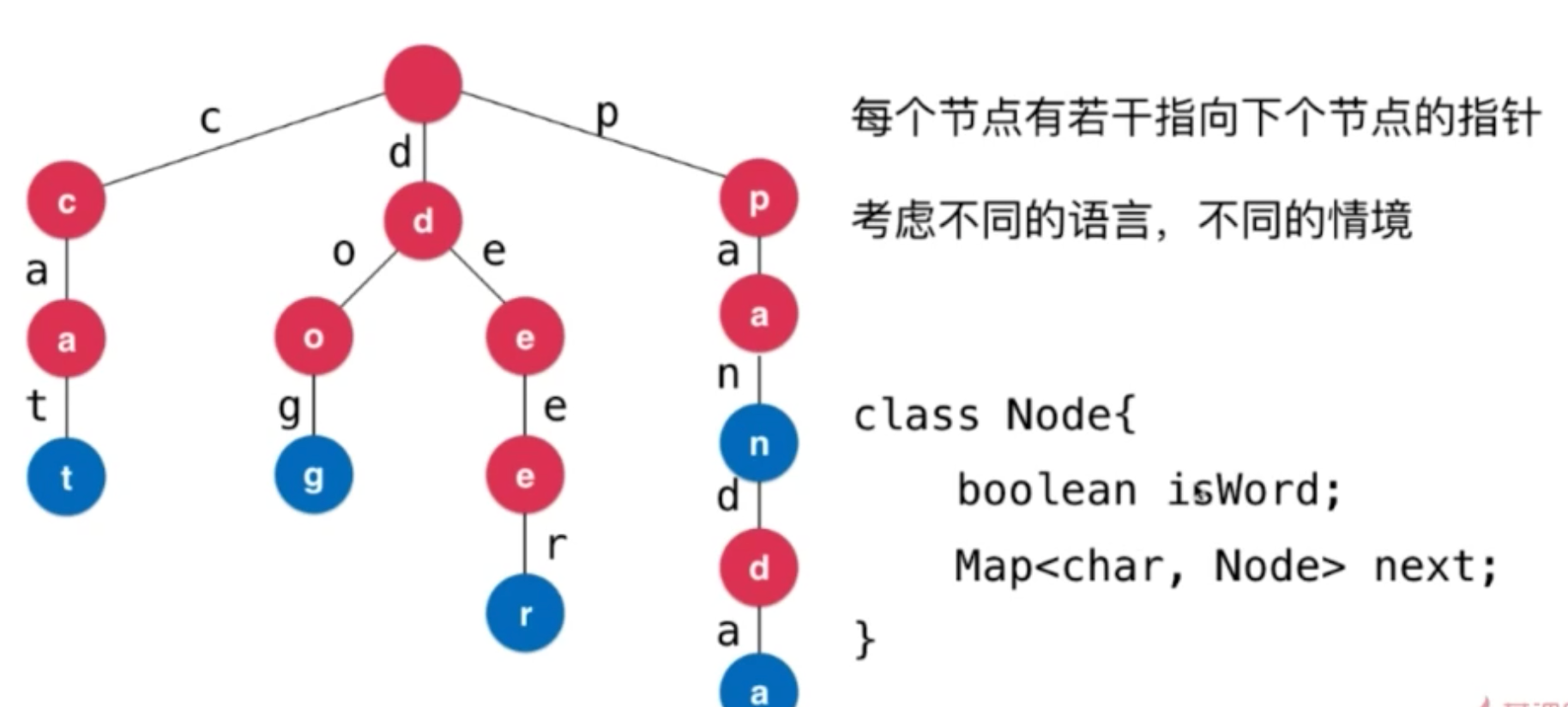
1.2 字典树结构

1.2.1 创建Trie

import java.util.TreeMap;

public class Trie {

    private class Node{

        public boolean isWord;
        public TreeMap<Character, Node> next;

        public Node(boolean isWord){
            this.isWord = isWord;
            next = new TreeMap<>();
        }

        public Node(){
            this(false);
        }
    }

    private Node root;
    private int size;

    public Trie(){
        root = new Node();
        size = 0;
    }

    // 获得Trie中存储的单词数量
    public int getSize(){
        return size;
    }

    // 向Trie中添加一个新的单词word
    public void add(String word){

        Node cur = root;
        for(int i = 0 ; i < word.length() ; i ++){
            char c = word.charAt(i);
            if(cur.next.get(c) == null)
                cur.next.put(c, new Node());
            cur = cur.next.get(c);
        }

        if(!cur.isWord){
            cur.isWord = true;
            size ++;
        }
    }
}

1.2.2 Trie查询

    // 查询单词word是否在Trie中
    public boolean contains(String word){

        Node cur = root;
        for(int i = 0 ; i < word.length() ; i ++){
            char c = word.charAt(i);
            if(cur.next.get(c) == null)
                return false;
            cur = cur.next.get(c);
        }
        //查询到了，但是有可能不是终止，pan  pandas
        //所以不能直接返回true
        return cur.isWord;
    }

三、并查集

子节点 —> 父节点的数结构

并查集可以应用到很多点之间是否有连接的问题
(脉脉，各个用户一层层之间连接)
在这里插入图片描述
是否连接问题(A–>B : T/F) & 路径问题(A----->X----->Z----->E------>B)
减少多余的计算

public interface UF {

    int getSize();
    boolean isConnected(int p, int q); //不关心pq是谁，可以直接存索引
    void unionElements(int p, int q);
}

并不考虑add 操作，一般都是一次性初始化

3.1 并查集的实现

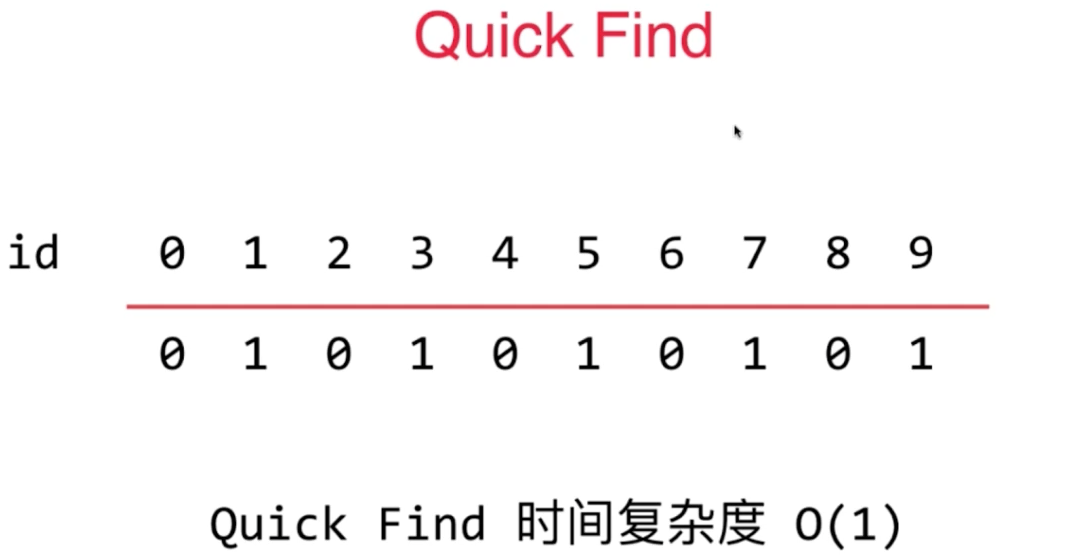
在这里插入图片描述

下边 0 1 代表在0 1 的集合中

在这里插入图片描述
一组集合，看是否在同一个下面的 0 1 中，

3.1.1 QuickFind

在这里插入图片描述


    // 查找元素p所对应的集合编号
    // O(1)复杂度
    private int find(int p) {
        if(p < 0 || p >= id.length)
            throw new IllegalArgumentException("p is out of bound.");

        return id[p];
    }

    // 查看元素p和元素q是否所属一个集合
    // O(1)复杂度
    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

在这里插入图片描述
union(1,4):1 和 4 在同一个集合中，因此需要改变4组的下面的值
时间复杂度O(n)

    // 合并元素p和元素q所属的集合
    // O(n) 复杂度
    @Override
    public void unionElements(int p, int q) {

        int pID = find(p);
        int qID = find(q);

        if (pID == qID)
            return;

        // 合并过程需要遍历一遍所有元素, 将两个元素的所属集合编号合并
        for (int i = 0; i < id.length; i++)
            if (id[i] == pID)
                id[i] = qID;
    }

3.1.1 QuickUnion

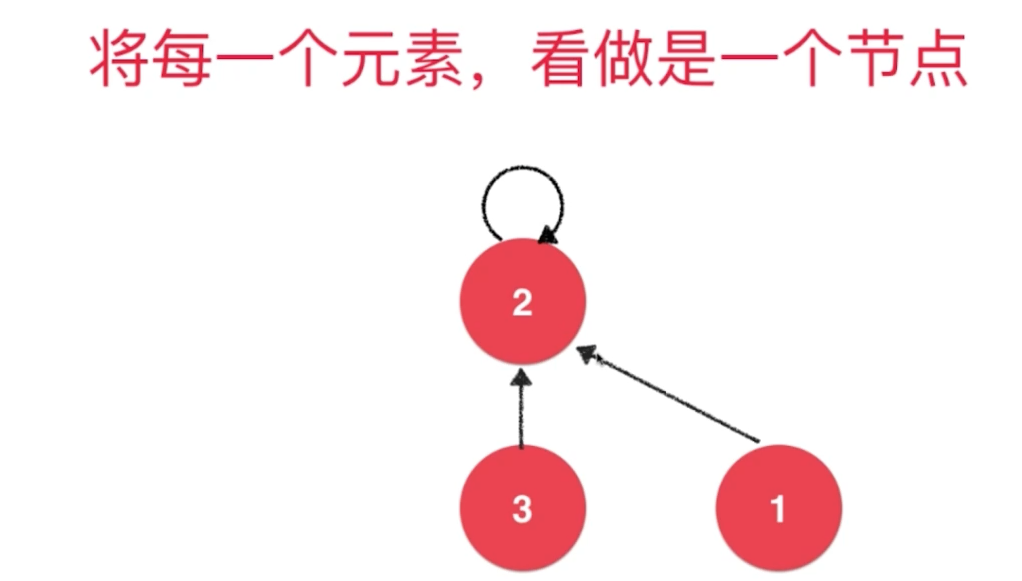
在这里插入图片描述
3 ----> 2 根节点
union(3,1)
1 ----> 2 根节点

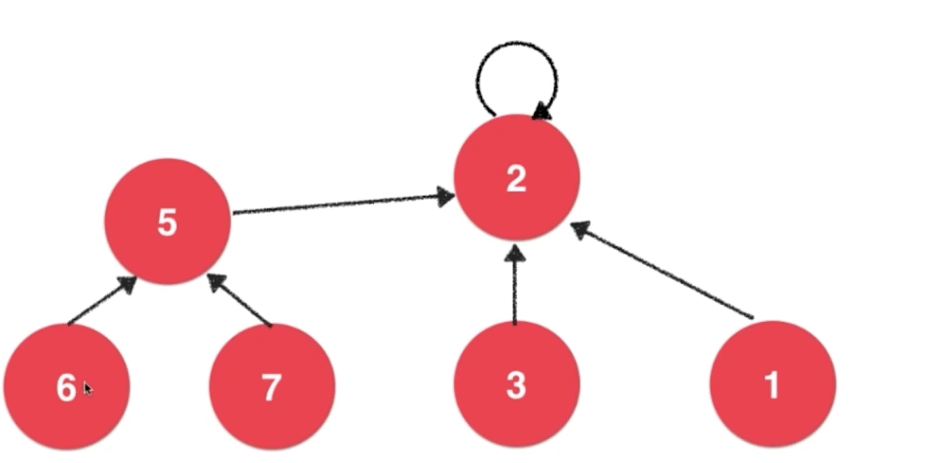
在这里插入图片描述
union(7,3)
7的根节点5 -----> 3的根节点

初始化

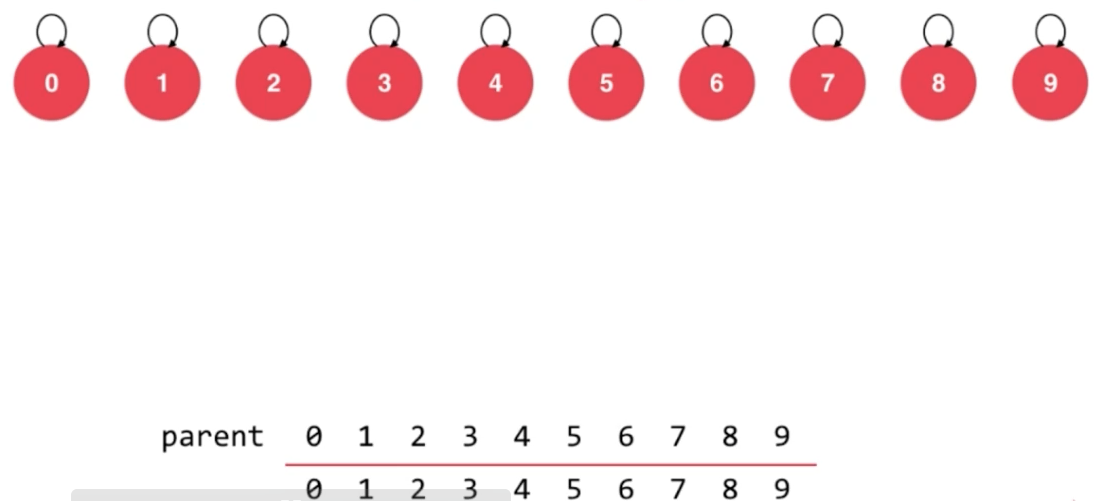
在这里插入图片描述
每个节点父节点都是自己

union示例

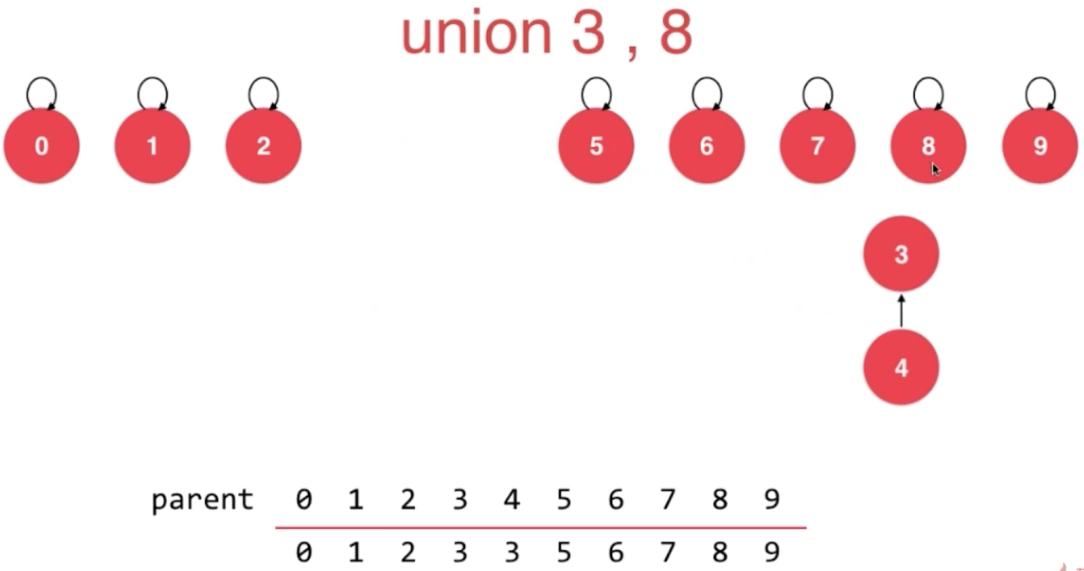
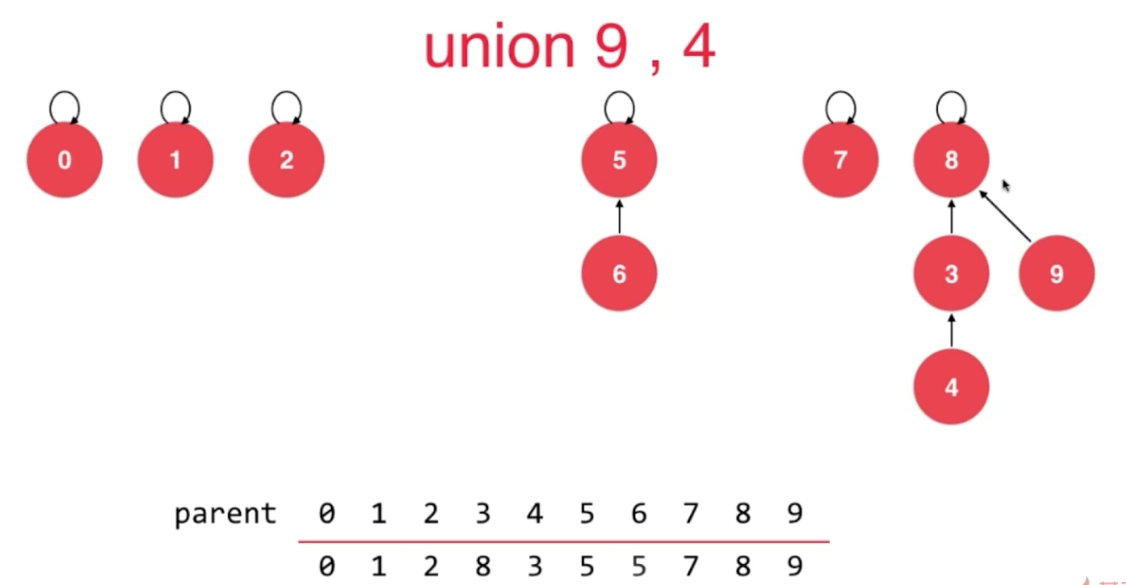
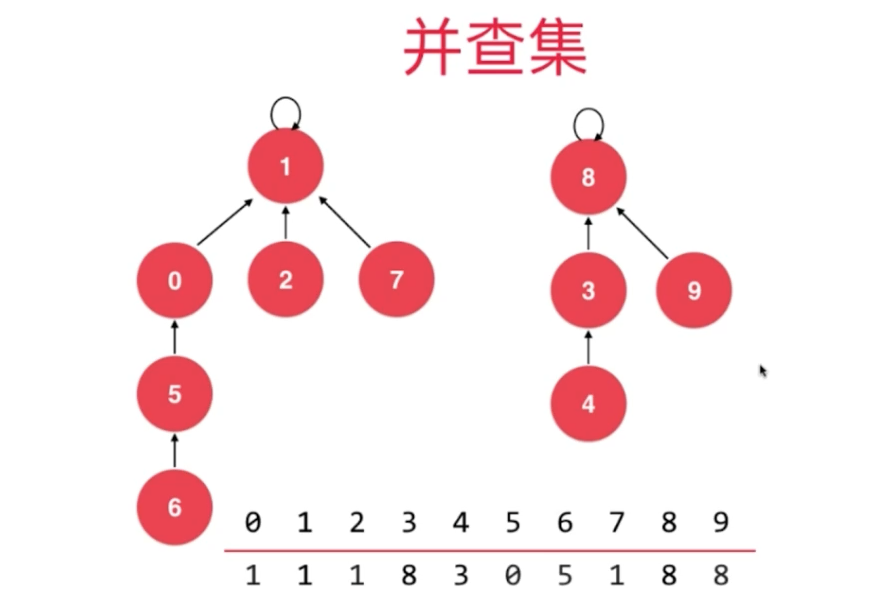
在这里插入图片描述

// 我们的第二版Union-Find
public class UnionFind2 implements UF {

    // 我们的第二版Union-Find, 使用一个数组构建一棵指向父节点的树
    // parent[i]表示第一个元素所指向的父节点
    private int[] parent;

    // 构造函数
    public UnionFind2(int size){

        parent = new int[size];

        // 初始化, 每一个parent[i]指向自己, 表示每一个元素自己自成一个集合
        for( int i = 0 ; i < size ; i ++ )
            parent[i] = i;
    }

    @Override
    public int getSize(){
        return parent.length;
    }

    // 查找过程, 查找元素p所对应的集合编号
    // O(h)复杂度, h为树的高度
    private int find(int p){
        if(p < 0 || p >= parent.length)
            throw new IllegalArgumentException("p is out of bound.");

        // 不断去查询自己的父亲节点, 直到到达根节点
        // 根节点的特点: parent[p] == p
        while(p != parent[p])
            p = parent[p];
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度, h为树的高度
    @Override
    public boolean isConnected( int p , int q ){
        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O(h)复杂度, h为树的高度
    @Override
    public void unionElements(int p, int q){

        int pRoot = find(p);
        int qRoot = find(q);

        if( pRoot == qRoot )
            return;

        parent[pRoot] = qRoot;
    }
}