第一题：子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

提示：

• 1 <= nums.length <= 10
• -10 <= nums[i] <= 10
• nums 中的所有元素 互不相同

解题思路：

任意一个子集，都可以用全部数组元素，每个元素包含，或不包含来表示。假如包含记为1，不包含记为0。如 [1, 2, 3] ，那么可以表示为

子集	0/1序列
[]	000
[1]	001
[2]	010
[3]	100
[1, 2]	011
[1, 3]	101
[2, 3]	110
[1, 2, 3]	111

可以发现 0/1 序列二进制数的范围，刚好是十进制从 0 到 $2^n-1$。那么，我们要做的，其实就只是把这个范围的数，按二进制，取每一位的数字，如果为1，表示原数组同样的索引位置，存放的元素存在子集中

1. 从 $0$ 开始遍历到 $2^n-1$，即 0/1 序列的十进制数。
   其中 $2^n$ 使用二进制表示，即第 n 位为 1 ，其他位为 0 的数。可以使用 1<< n 来表示。
   如：二进制数 100000 共有 6 位，转换为十进制即 $2^6$，也即 1 左移 6 位。
2. 每次遍历的 0/1 序列数，转换为二进制数后，取每一位数字。这里每一位，即 0 到 数组长度 的位数来取。取一个数 x ，二进制的第 j 位，可以把 x 右移 j 位，再和 1 进行按位与操作。如 50 ，二进制即 110010 ，第 0 位为最后一位，那么，要取第 1 位（即倒数第二位）的 1，可以先右移 1位，即 50 >> 1 ，得到 11001，然后和1按位与计算
3. 第二步取得的每一位数字，如果是1，则去原数组该索引位置获取元素，保存子集中

代码实现：

class Solution {
    public List<List<Integer>> subsets(int[] nums) {
        int n = nums.length;
        List<List<Integer>> subset = new ArrayList<>();
        for(int i = 0;i < (1 << n);i++) {
            List<Integer> sub = new ArrayList<>();
            for(int j = 0;j < n;j++) {
                if(((i >> j) & 1) == 1) {
                    sub.add(nums[j]);
                }
            }
            subset.add(sub);
        }
        return subset;
    }
}

第二题：组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。

示例 1：

输入：n = 4, k = 2
输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

示例 2：

输入：n = 1, k = 1
输出：[[1]]

提示：

• 1 <= n <= 20
• 1 <= k <= n

解题思路：

假如 n=4, k=2 ，即要在 [1, 2, 3, 4] 中求 2 个数的组合。
那么对每个组合来说， 1~4 范围内的每个数字都只有 包含 与 不包含 两种情况
则 dfs(1, 4) 可以分解为 dfs(1) 的组合与 dfs(2, 4) 组合：
（1） dfs(1) 为 1 的组合，即 [1] （包含 1 ）、 [] （不包含 1 ）。
（2）如果 dfs(1) 包含1，则 dfs(2, 4) 需要有 k-1=2-1=1 个元素来构建组合
（3）如果 dfs(1) 不包含1，则 dfs(2, 4) 需要有 k-0=2 个元素来构建组合

同样的， dfs(2, 4) = dfs(2) + dfs(3, 4) dfs(3, 4) = dfs(3) + dfs(4) 。

由以上分解的问题，最终可以采取如下步骤：

1. 从1开始遍历到4，求取组合，保存在 List<List< Integer > > ，记为 ret 。
2. 搜索到的组合保存在一个双端队列 Deque 中，记为 sub ，如果 sub 长度为 k ，则保存 sub 到 ret 。
3. 每次遍历，先包含当前数字 cur ，即 sub 添加 cur ；同时进一步求解子问题 cur+1 到 n 的组合。这里最终的组合都包含 cur 。
4. 求不包含当前数字 cur 的组合，所以还需要把 sub 中最后的元素 cur 删除；同时进一步求解子问题 cur+1到 n 的组合。这里最终组合都不包含 cur

代码实现：

class Solution {
      List<List<Integer>> ret = new ArrayList<>();
      Deque<Integer> sub = new ArrayDeque<>();
    public List<List<Integer>> combine(int n, int k) {
        dfs(n,k,1);
        return ret;
    }
    private void dfs(int n,int k,int cur) {
        if(sub.size() == k) {
            ret.add(new ArrayList(sub));
            return;
        }
        for(int i = cur;i <= n;i++) {
            sub.addLast(i);
            dfs(n,k,i+1);
            sub.removeLast();
        }
    } 
}

第三题：全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

输入：nums = [0,1]
输出：[[0,1],[1,0]]

示例 3：

输入：nums = [1]
输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

解题思路：

本题为一个回溯问题，实际上就是一个决策树的遍历过程。

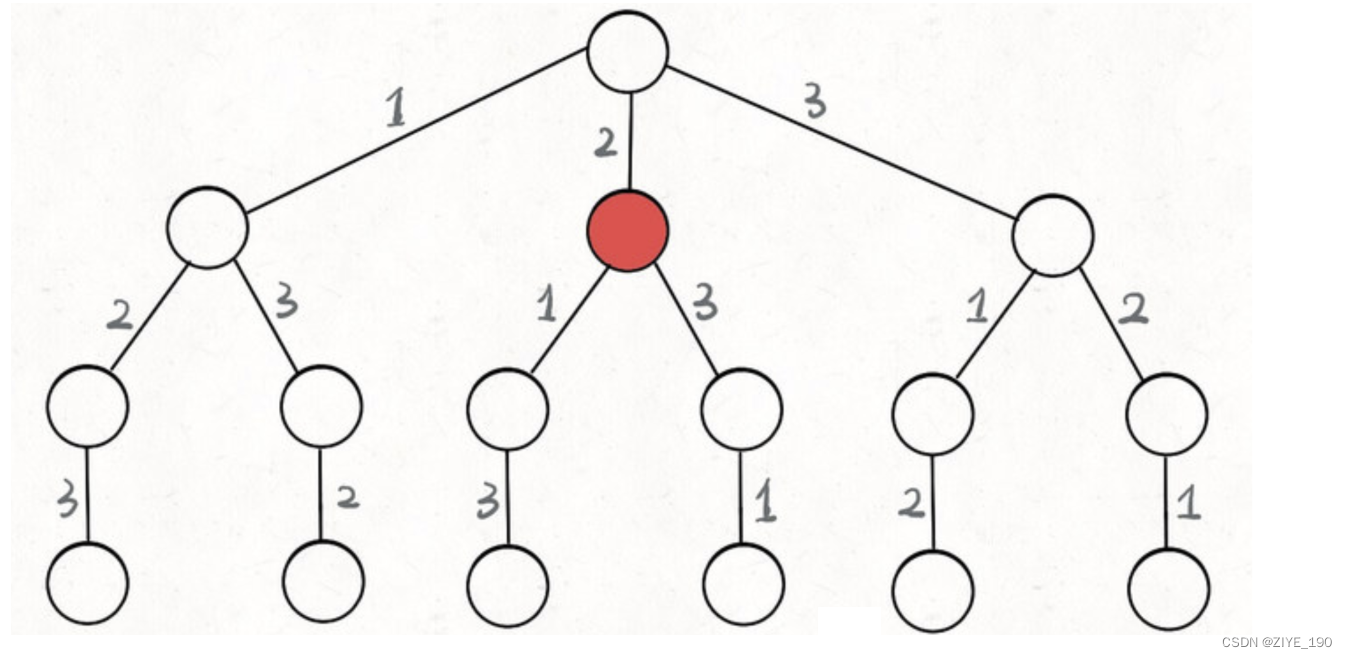
1. 路径：用双向队列sub接收已经做出的选择。
2. 选择列表：当前可以做的选择。
3. 结束条件：当sub的大小等于nums时，无法再做选择。

代码实现：

class Solution {
    List<List<Integer>> ret = new ArrayList<>();
    Deque<Integer> sub = new ArrayDeque<>();
    public List<List<Integer>> permute(int[] nums) {
        backTrack(nums);
        return ret;
    }
    private void backTrack(int[] nums) {
        if(sub.size() == nums.length) {
            ret.add(new ArrayList(sub));
            return;
        }
        for(int i = 0;i < nums.length;i++) {
            if(!sub.contains(nums[i])) {
            sub.addLast(nums[i]);
            backTrack(nums);
            sub.removeLast(); 
            }
        }
    }
}

第四题：全排列II

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

示例 2：

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

解题思路：

数组中包含了重复的数字，要求我们返回不重复的全排列，那么，我们可以将数组升序排序，这样如果相邻元素一样，在决策树就可以不选择同一层中，和上一个相同的元素

要判断同一层中的相邻元素，即数组相邻元素是否一样，需要再维护一个数组每个元素状态的列表：可以设置为boolean 数组，长度和原数组一样，当已选择，则同索引上的状态设为 true 。这样，我们在路径中，选择元素时，就可以不选择：

1. 已选择该元素，不再选择
2. 同一层相邻的上一个元素，和当前元素相等，且上一个元素未选择，则当前元素也不选择

代码实现：

class Solution {
    List<List<Integer>> ret = new ArrayList<>();
    Deque<Integer> sub = new ArrayDeque<>();
    boolean[] visits;
    public List<List<Integer>> permuteUnique(int[] nums) {
        visits = new boolean[nums.length];
        Arrays.sort(nums);
        backTrack(nums);
        return ret;
    }
    private void backTrack(int[] nums) {
        if(sub.size() == nums.length) {
            ret.add(new ArrayList(sub));
            return;
        }
        for(int i = 0;i < nums.length;i++) {
           if(visits[i] ||(i > 0 && nums[i] == nums[i-1] && !visits[i-1])) {
               continue;
           }
            sub.addLast(nums[i]);
            visits[i] = true;
            backTrack(nums);
            sub.removeLast(); 
            visits[i] = false;
        }
    }
}

第五题：括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例 1：

输入：n = 3
输出：[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”]

示例 2：

输入：n = 1
输出：[“()”]

提示：

• 1 <= n <= 8

解题思路：

本题属于全排列的一种变形，可以看出，输出的结果，为 n 个左括号，与 n 个右括号，在满足 左括号必须以正确的顺序闭合条件下的全排列。
本题使用搜索回溯算法+剪枝来实现

• 当前左右括号都有大于 0 个可以使用的时候，才产生分支；
• 产生左分支的时候，只看当前是否还有左括号可以使用；
• 产生右分支的时候，需要已选择的左括号数量大于已选择的右括号数量；
• 递归结束条件：在左边和右边剩余的括号数都等于 0的时候

代码实现：

class Solution {
    List<String> ret = new ArrayList<>();
    StringBuilder path = new StringBuilder();
    public List<String> generateParenthesis(int n) {
        backtrack(n,0,0);
        return ret;
    }
    private void backtrack(int n,int left,int right) {
        if(path.length() == n*2) {
            ret.add(path.toString());
            return;
        }   
        if(left < n) {
            path.append('(');
            backtrack(n,left+1,right);
            path.deleteCharAt(path.length()-1);
        }
        if(right < left) {
            path.append(')');
            backtrack(n,left,right+1);
            path.deleteCharAt(path.length()-1);
        }
    }
}