目录
- 前言
- 题目
- 1.按照二叉搜索树特性遍历整棵二叉搜索树,
- 2. 本题思路分析:
- 3. 算法实现
- 4. 算法坑点
前言
我在刷卡哥的“代码随想录”,自己的总结笔记均会放在“算法刷题-代码随想录”该专栏下。
代码随想录此题链接
题目
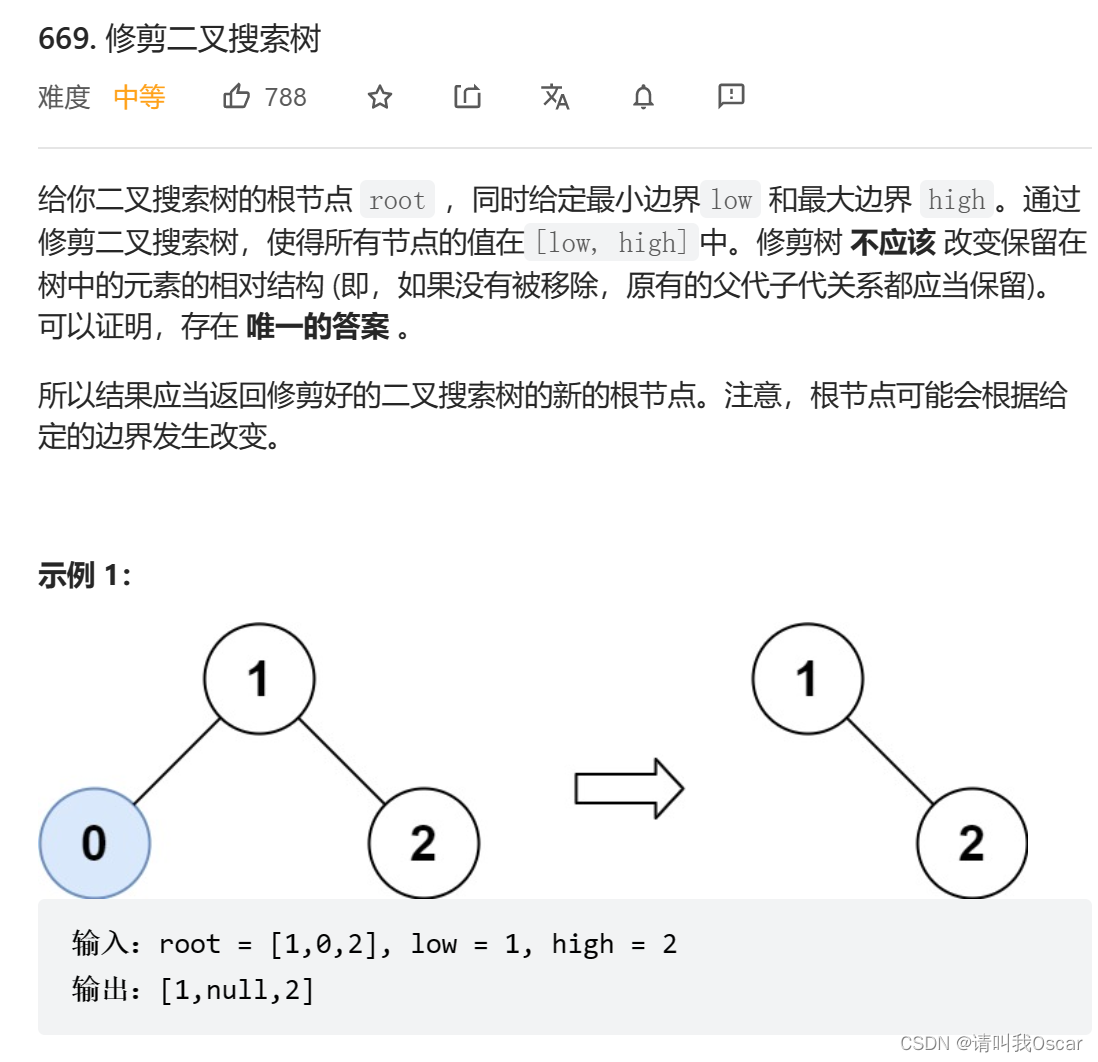
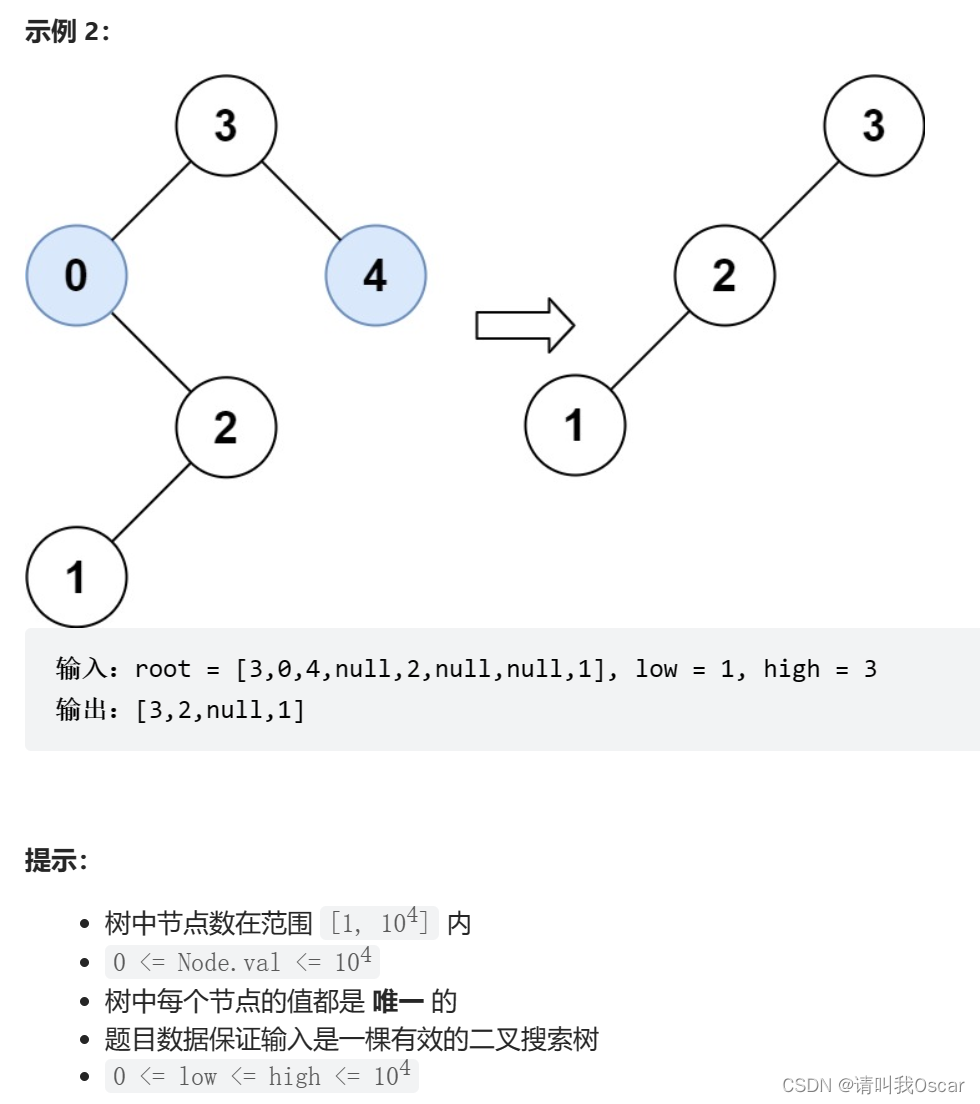
1.按照二叉搜索树特性遍历整棵二叉搜索树,
在遍历过程中,替换掉其中不满足条件的二叉搜索树的节点。
2. 本题思路分析:
递归三部曲:
- 参数与返回值:
- 参数:当前节点cur和需要保留的上下区间边界值:low,high。
- 返回值:返回TreeNode类型对象
- 终止条件:当前节点为null,说明遍历结束,直接返回null即可。
- 单层循环逻辑:
- 如果当前节点的值小于low,则说明该节点应该删除,但是有可能该节点的右孩子节点在区间内,所以应该把该节点的右孩子节点替代该节点。递归写法就应该是递归函数带上当前节点的右孩子为参数,返回结果直接赋值给当前节点(相当于替换了用右孩子替换了当前节点,并返回替换后的当前节点(现在其实已经是右孩子了))。
- 如果当前节点的值大于high,则说明该节点应该删除,但是有可能该节点的左孩子节点在区间内,所以应该把该节点的左孩子节点替代该节点。递归写法就应该是递归函数带上当前节点的左孩子为参数,返回结果直接赋值给当前节点(相当于替换了用左孩子替换了当前节点,并返回替换后的当前节点(现在其实已经是左孩子了))。
- 正常递归(遍历整个二叉搜索树的步骤),将递归函数带上当前节点的左孩子节点,并将返回值赋值给当前节点的左孩子;将递归函数带上当前节点的右孩子节点,并将返回值赋值给当前节点的右孩子;
- 最后返回这个当前节点。
3. 算法实现
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null){
return null;
}
if(root.val < low){
root = trimBST(root.right,low,high);
return root;
}else if(root.val > high){
root = trimBST(root.left,low,high);
return root;
}
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
return root;
}
}
以下为优化写法
class Solution {
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null){
return null;
}
if(root.val < low){
return trimBST(root.right,low,high);
}else if(root.val > high){
return trimBST(root.left,low,high);
}
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);
return root;
}
}
4. 算法坑点
- 本题,最主要的是理解,修建二叉搜索树是在遇到不满足节点时,将它可能满足条件的某一边的孩子节点与它替换。
if(root.val < low){
root = trimBST(root.right,low,high);
return root;
}else if(root.val > high){
root = trimBST(root.left,low,high);
return root;
}
- 并且记得要有常规遍历整个二叉搜索树的过程。
root.left = trimBST(root.left,low,high);
root.right = trimBST(root.right,low,high);