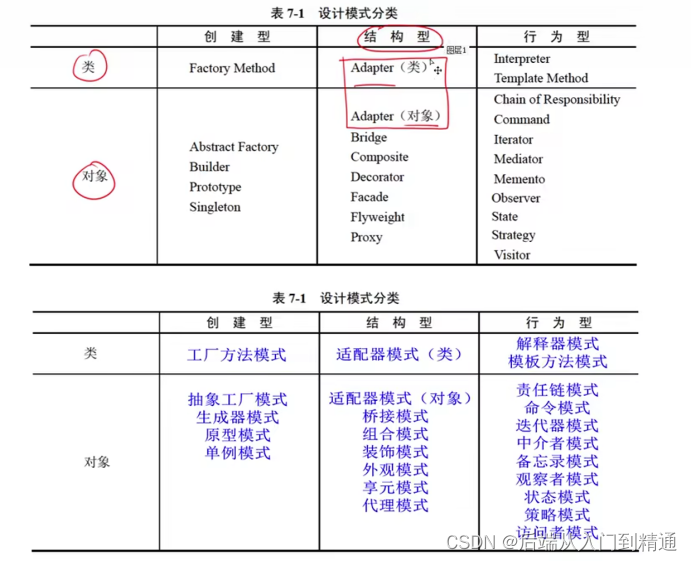
线段树的结构
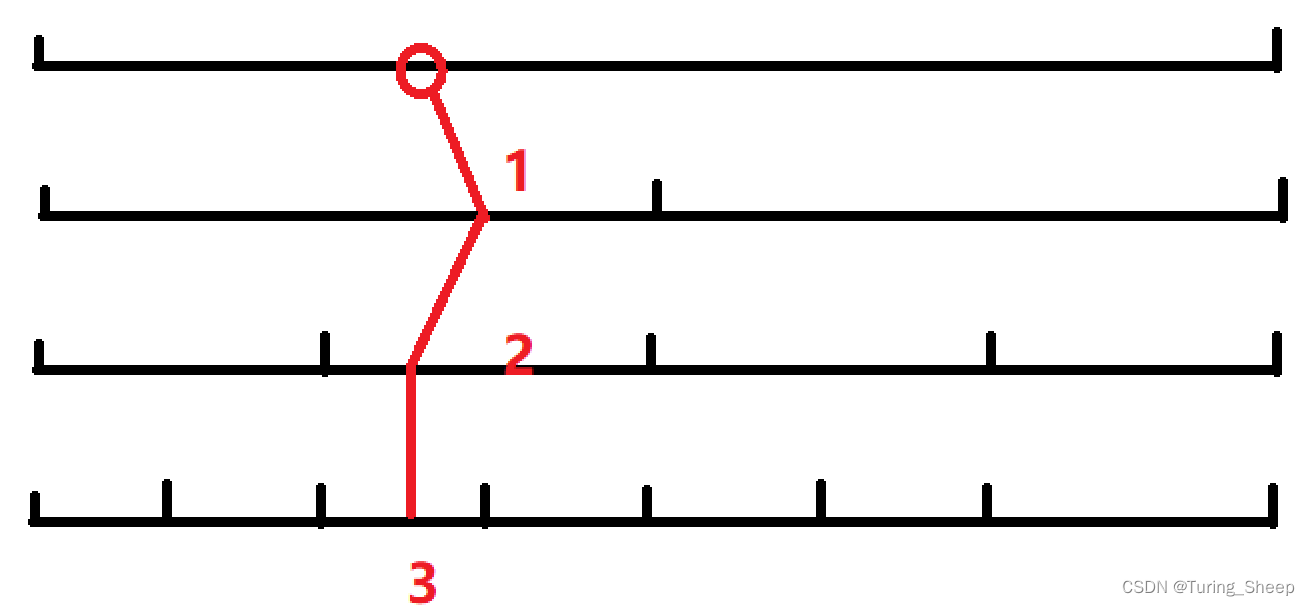
线段树是一棵二叉树,其结点是一条“线段”——[a,b],它的左儿子和右儿子分别是这条线段的左半段和右半段,即[a, (a+b)/2 ]和[(a+b)/2 ,b]。线段树的叶子结点是长度为1的单位线段[a,a+1]。下图就是一棵根为[1,10]的线段树:
易证一棵以[a,b]为根的线段树结点数是2*(b-a)-1。由于线段树是一棵平衡树,因此一棵以[a,b]为根结点的线段树的深度为log2(2*(b-a))。
线段树中的结点一般采取如下数据结构:
其中a,b分别表示线段的左端点和右端点,Left,Right表示左儿子和右儿子的编号。因此我们可以用一个一维数组来表示一棵线段树:
Tree:array[1..Maxn] of TreeNode;
a,b,Left,Right这4个域是描述一棵线段树所必须的4个量。根据实际需要,我们可以增加其它的域,例如增加Cover域来计算该线段被覆盖的次数,bj域用来表示结点的修改标记(后面将会提到)等等。
线段树的建立
我们可以用一个简单的过程建立一棵线段树。

线段树中的线段插入和删除
增加一个Cover的域来计算一条线段被覆盖的次数,即数据结构变为:

因此在MakeTree的时候应顺便把Cover置0。
线段的插入
插入一条线段[c,d]

线段的删除
删除一条线段[c,d]

线段树的简单应用
掌握了线段树的建立,插入和删除这3条操作,就能用线段树解决一些最基本的统计问题了。例如给出一系列线段[a,b] (0< a < b < 10000)覆盖在数轴上,然后求该数轴上共有多少个单位长度[k,k+1]被覆盖了。我们便可以在读入一系列线段[a,b]的时候,同时调用过程Insert(1)。等所有线段都插入完后,就可以进行统计了:

像这样的基本静态统计问题,线段树是可以很方便快捷地解决的。但是我们会留意到,如果处理一些动态统计问题,比如说一些需要用到删除和修改的统计,困难就出现了。
『例1』
在数轴上进行一系列操作。每次操作有两种类型,一种是在线段[a,b]上涂上颜色,另一种将[a,b]上的颜色擦去。问经过一系列的操作后,有多少条单位线段[k,k+1]被涂上了颜色。
这时我们就面临了一个问题——线段的删除。但线段树中线段的删除只能是把已经放入的线段删掉,例如我们没有放置[3,6]这条线段,删除[3,6]就是无法做到的了。而这道题目则不同,例如在[1,15]上涂了颜色,我们可以把[4,9]上的颜色擦去,但线段树中只是插入了[1,15]这条线段,要删除[4,9]这条线段显然是做不到的。因此,我们有必要对线段树进行改进。
线段树的改进
【关键词:状态下沉,标志向下扩散】
用回刚刚那个例子。给[1,15]涂上色后,再把[4,9]的颜色擦去。很明显[1,15]这条线段已经不复存在,只剩下[1,4]和[9,15],所以我们必须对线段树进行修改,才能使它符合改变了的现实。我们不难想到把[1,15]这条线段删去,再插入线段[1,4]和[9,15]。但事实上并非如此简单。如下图:
若先前我们已经插入了线段[8,11],[1,8]。按上面的做法,只把[1,15]删去,然后插入[1,4],[9,15]的话,[1,8],[8,11]这两条线段并没有删去,但明显与实际不符了。于是[1,8],[8,11]也要修改。这时疑问就来了。若以线段[1,15]为根的整棵线段树中的所有结点之前都已经插入过,即我们曾经这样涂过颜色:[1,2],[2,3],……,[14,15],[1,3],[3,5],……,[13,15],[1,5],…………,[1,15]。然后把[1,15]上的颜色擦去。那么整个线段树中的所有结点的状态就都与实际不符了,全都需要修改。修改的复杂度就是线段树的结点数,即2*(15-1)=28。如果不是[1,15]这样的小线段,而是[1,30000]这样的线段,一个擦除动作就需要O(59998)的复杂度去修改,显然效率十分低(比直接模拟的O(30000)还差)。
为了解决这个问题,我们给线段树的每一个结点增加一个标记域(以下用bj来表示标记域)。增加一个标记域有什么用呢?如下图:
以[1,5]为根的整棵线段树的全部结点都已涂色。现把[1,5]上的颜色擦去。则整棵线段树的结点的状态都与实际不符了。可是我们并不一定要对所有结点都进行修改,因为有些结点以后可能根本不会有被用到的时候。例如我们做完擦去[1,5]的操作之后,只是想询问[3,5]是否有涂上颜色。那么我们对[1,2],[2,3],[1,3],[3,4],[4,5]等线段的修改就变成无用功了。为了避免无用功的出现,我们引入标记域bj。具体操作如下:
1、擦去线段[a,b]之后,给它的左儿子和右儿子都做上标记,令它们的bj=-1。
2、每次访问一条线段,首先检查它是否被标记,若其bj=-1,则进行如下操作:
①将该线段的状态改为未被覆盖,并把该线段设为未被标记,bj=0。
②把该线段的左右儿子都设为被标记,bj=-1。
对线段[1,5]进行了这样的操作后就不需要对整棵线段树都进行修改了。原理很简单。以线段[3,4]为例。若以后有必要访问[3,4],则必然先访问到它的父亲[3,5],而[3,5]的bj=-1,因此进行①、②的操作后,[3,5]的状态变为未被覆盖,并且把他的标记传递给了他的儿子——[3,4]和[4,5]。接着访问[3,4]的时候,它的bj=-1,我们又把[3,4]的状态变为未被覆盖。可见,标记会顺着访问[3,4]的路一直传递到[3,4],使得我们知道要对[3,4]的状态进行修改,避免了错误的产生。同时,当我们需要用到[3,4]的时候才会进行修改,如果根本不需要用它,修不修改都无所谓了,并不会影响程序的正确性。因此这种方法在保持了正确性的同时有避免了无意义的操作,提高了程序的效率。
进行标记更新的代码如下:

每次访问线段[a,b]之前,首先检查它是否被标记,如果是则调用过程Clear进行状态修改。这样做只是在访问的时候顺便进行修改,复杂度是O(1),程序效率依然很高。
于是,引入标记域后,本题中插入和删除的过程大致如下:
插入过程 Insert
1、若该线段被标记,则调用Clear过程
2、若线段状态为被涂色,则退出过程(线段已被涂色,无需再插入它或它的子线段)
3、若涂色的区域覆盖了该线段,则该线段的状态变为被涂色,并退出过程
4、若涂色的区域与该线段的左半截的交集非空,则调用左儿子的插入过程
5、若涂色的区域与该线段的右半截的交集非空,则调用右儿子的插入过程
删除过程 Delete

1、若该线段被标记,则退出过程(该线段已被赋予被擦除的“义务”,无需再次赋予)
2、若擦除的区域覆盖了该线段,则该线段的状态变为未被涂色,并将其左右儿子都做上标记,退出过程
3、若该线段的状态为被涂色,则
① 该线段状态变为未被涂色
② 将其左右儿子做上标记
③ 插入线段[a,c]和[d,b]
4、若该线段的状态为未被涂色,则
①若擦除区域与该线段的左半截的交集非空,则调用左儿子的擦除过程
②若擦除区域与该线段的右半截的交集非空,则调用右儿子的擦除过程
归纳一下标记域的思想及如何使用。如果我们对整条线段[a,b]进行操作的话,我们就可以只是给[a,b]的左右儿子做上标记,而无需对以[a,b]为根的整棵子树中的所有结点进行修改。原理就是对下面的所有结点[c,d],都有[c,d] [a,b],因此[a,b]状态的改变也就代表了[c,d]状态的改变。
本着这个思想,标记域的使用形式并不是固定的,而是多样的,具体形式如何要视题目而定,但只要理解了它的思想,总能想到如何确定作标记的方式,维持线段树的高效。