【MATLAB图像处理实用案例详解（10）】——基于Kalman滤波的目标跟踪预测红色小球位置

news2025/6/15 17:53:11

一、Kalman滤波

Kalman 滤波算法是一个最优化自回归数据处理算法，对于很多问题的解決，它是最优、效率最高甚至是最有用的。Kalman 滤波的广泛应用己经超过30年，领域包括机器人导航、控制、传感器数据融合以及军事方面的雷达系统、导弹追踪等。近年来 Kalman 滤波被应用于数宇图像处理，例如人脸识别、图像分割、目标跟踪、图像边缘检测等。
首先要引入一个离散控制过程的系统，该系统可用一个线性随机微分方程来描述：
$X (k) = A X (k - 1) + B U (k) + W (k)$
系统的测量值为：
$Z (k) = H X (k) + V (k)$
上面两个式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。A和B是系统参数，对于多模型系统，它们为矩阵。Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。它们被假设成高斯白噪声，其协方差分别是Q和R（这里假设它们不随系统状态变化而变化）。
对于满足上面条件的线性微分系统，Kalman滤波器是最优的闲心处理器。下面用Kalman滤波器来估计系统的最优化输出。
首先利用系统的过程模型来预测下一状态的系统。假设现在的系统状态是k，根据系统的模型，基于系统的上衣状态可以预测出现在状态：
$X (k ∣ k - 1) = A X (k - 1∣ k - 1) + B U (k)$
上式中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。
到现在为止，系统结果已经更新，可是对应于X(k|k-1)的协方差还没有更新。用P表示协方差。
$P (k ∣ k - 1) = A P (k - 1∣ k - 1) A^{'} + Q$
式中，P(k|k-1)是X(k|k-1)对应的协方差，P(k-1|k-1)是X(k-1|k-1)对应的协方差，A’表示A的转置矩阵，Q是系统过程的协方差。上式就是Kalman滤波器5个公式当中的前两个，也就是对系统的预测。
目前，已有现在状态的预测结果，然后再收集现在状态的测量值，结合预测值和测量值，就可以得到现在状态k的最优化估计值X(k|k)：
$X (k ∣ k) = X (k ∣ k - 1) + K g (k) (Z (k) - H X (k ∣ k - 1))$
上式中，Kg为卡尔曼增益：
$K g (k) = P (k ∣ k - 1) H^{'} / H P (k ∣ k - 1) H^{'} + R$
为了使Kalman滤波器不断地运行下去直到系统过程结束，还要更新k状态下X(k|k)的协方差：
P(k|k)=(I-Kg(k)H)P(k|k-1)
上式中，I为单位阵，对于单模型单测量，I=1。当系统进入k+1状态时，P(k|k)就是上式中的P(k-1|k-1).这样，算法就可以自回归的运算下去。

上面五个公式就是Kalman滤波的5个基本公式。

二、Kalman滤波源程序

Kalman滤波源程序如下：

%Kalman滤波
clear all
N=800;
w(1)=0;
%系统预测的随机白噪声
w=randn(1,N) 
x(1)=0;
a=1;
for k=2:N;
%系统的预测值
x(k)=a*x(k-1)+w(k-1); 
end
%测量值的随机白噪声
V=randn(1,N); 
q1=std(V);
Rvv=q1.^2;
q2=std(x);
Rxx=q2.^2;
q3=std(w);
Rww=q3.^2;
c=0.2;
%测量值
Y=c*x+V; 
p(1)=0;
s(1)=0;
for t=2:N;
%前一时刻X的协方差系数
p1(t)=a.^2*p(t-1)+Rww; 
%Kalman增益
b(t)=c*p1(t)/(c.^2*p1(t)+Rvv); 
%经过滤波后的信号
s(t)=a*s(t-1)+b(t)*(Y(t)-a*c*s(t-1)); 
%t状态下x(t|t)的协方差系数
p(t)=p1(t)-c*b(t)*p1(t); 
end
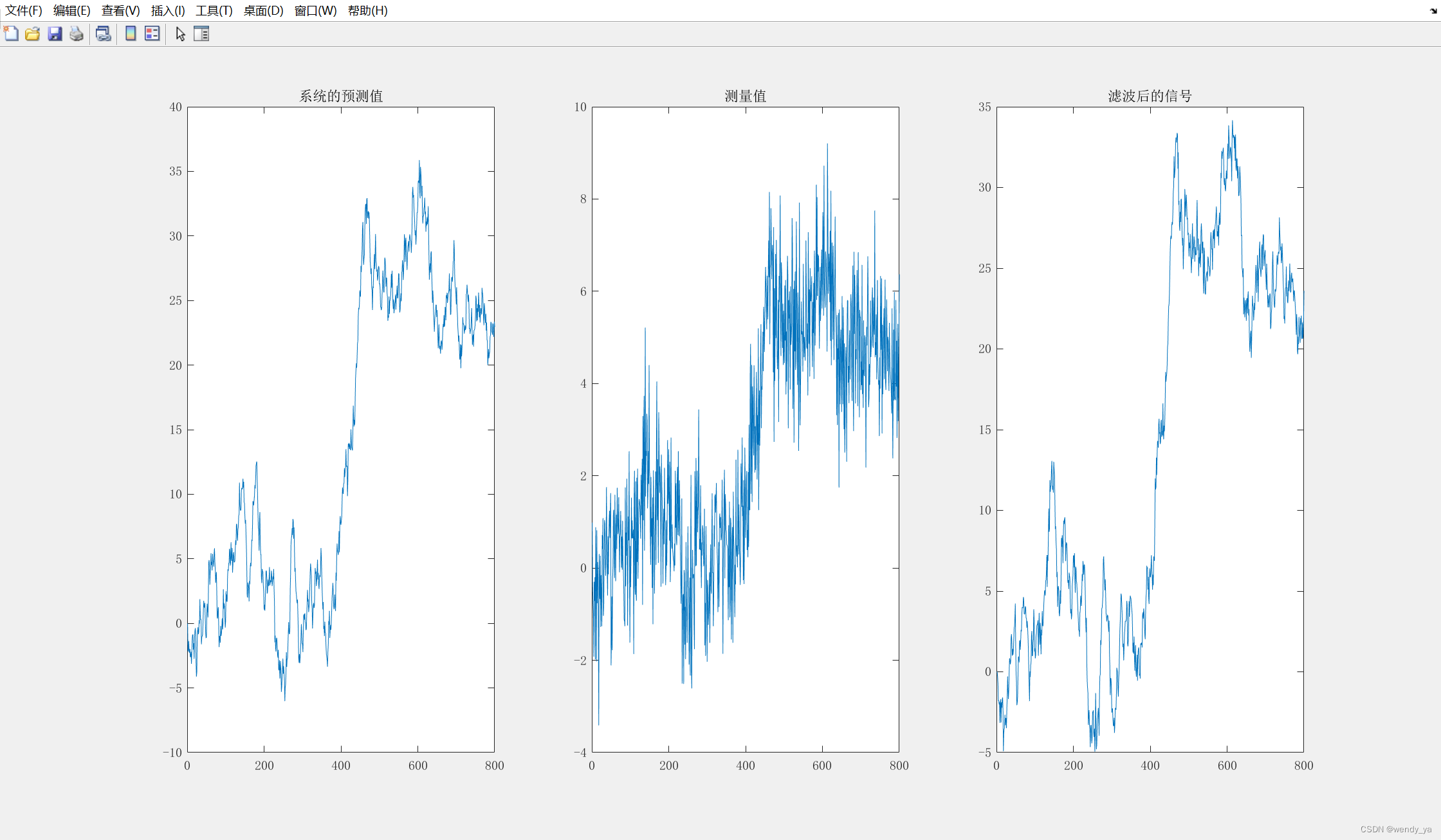
subplot(131)
plot(x)
title('系统的预测值')
subplot(132)
plot(Y)
title('测量值')
subplot(133)
plot(s)
title('滤波后的信号')

运行结果如下：
在这里插入图片描述

三、Kalman滤波预测红色小球位置程序实现

Kalman滤波是一种最优化递归处理算法，其具有如下特点：
①Kalman滤波充分利用如下信息估计感兴趣变量当前的取值：系统和测量装置的动态特性；系统噪声、测量误差和动态模型的不确定性的统计描述；感兴趣变量的初始条件的相关信息。
②Kalman滤波不需要保存先前的数据，当进行新的测量时也不需要对原来数据进行处理。
③Kalman滤波算法获得理想滤波效果的前提是，必须已知系统模型以及系统噪声和量测噪声的统计模型。
④Kalman滤波的噪声过程必须为零均值白噪声。

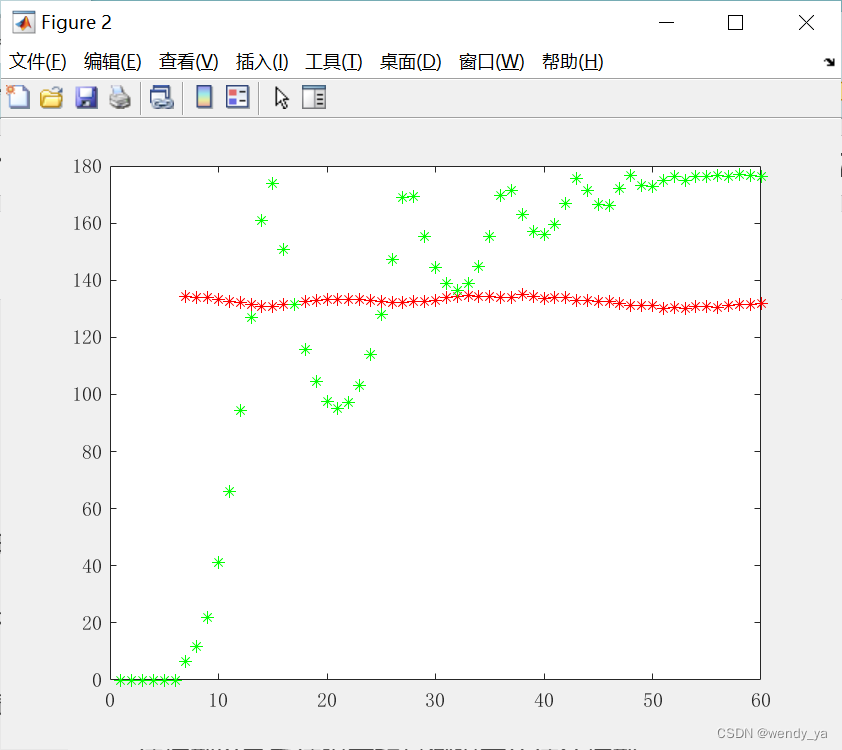
运行结果如下：
在这里插入图片描述
球横纵坐标的位置曲线如下：