一 二叉树入门
之前我们实现的符号表中,不难看出,符号表的增删查操作,随着元素个数N的增多,其耗时也是线性增多的,时间复杂度都是O(n),为了提高运算效率,接下来我们学习树这种数据结构。
1.1 树的基本定义
树是我们计算机中非常重要的一种数据结构,同时使用树这种数据结构,可以描述现实生活中的很多事物,例如家谱、单位的组织架构、等等。
树是由n(n>=1)个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
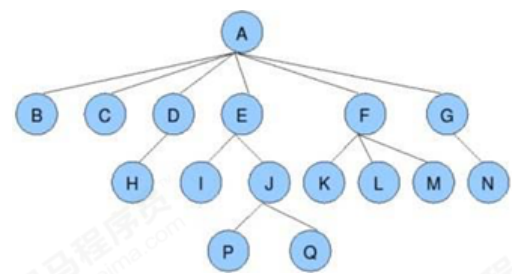
树具有以下特点:
- 每个结点有零个或多个子结点;
- 没有父结点的结点为根结点;
- 每一个非根结点只有一个父结点;
- 每个结点及其后代结点整体上可以看做是一棵树,称为当前结点的父结点的一个子树;
1.2 树的相关术语
结点的度:
一个结点含有的子树的个数称为该结点的度;
叶结点:
度为0的结点称为叶结点,也可以叫做终端结点
分支结点:
度不为0的结点称为分支结点,也可以叫做非终端结点
结点的层次:
从根结点开始,根结点的层次为1,根的直接后继层次为2,以此类推
结点的层序编号:
将树中的结点,按照从上层到下层,同层从左到右的次序排成一个线性序列,把他们编成连续的自然数。
树的度:
树中所有结点的度的最大值
树的高度(深度):
树中结点的最大层次
森林:
m(m>=0)个互不相交的树的集合,将一颗非空树的根结点删去,树就变成一个森林;给森林增加一个统一的根结点,森林就变成一棵树
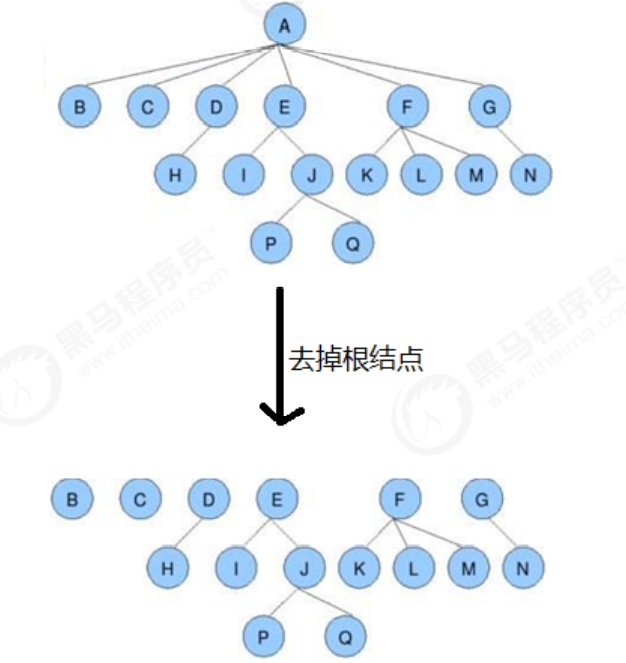
孩子结点:
一个结点的直接后继结点称为该结点的孩子结点
双亲结点(父结点):
一个结点的直接前驱称为该结点的双亲结点
兄弟结点:
同一双亲结点的孩子结点间互称兄弟结点
1.3 二叉树的基本定义
二叉树就是度不超过2的树(每个结点最多有两个子结点)
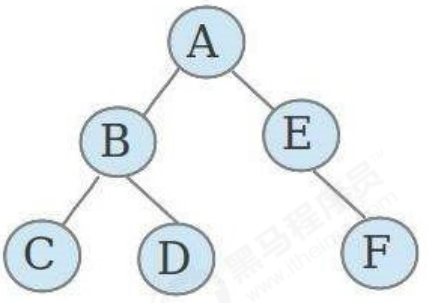
满二叉树:
一个二叉树,如果每一个层的结点树都达到最大值,则这个二叉树就是满二叉树
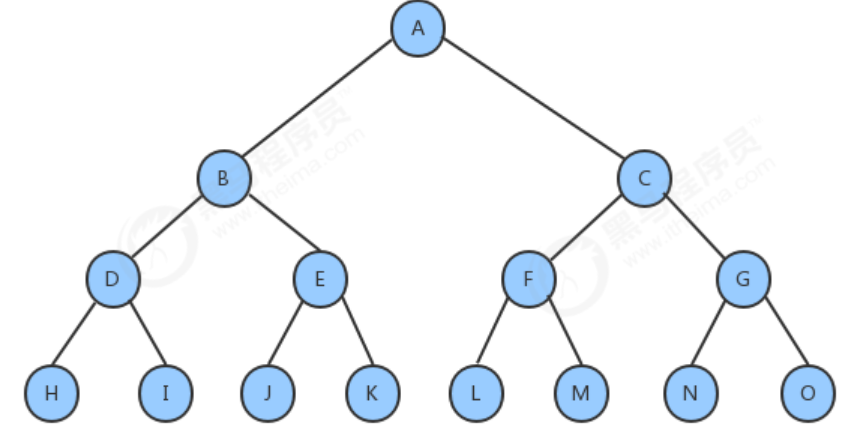
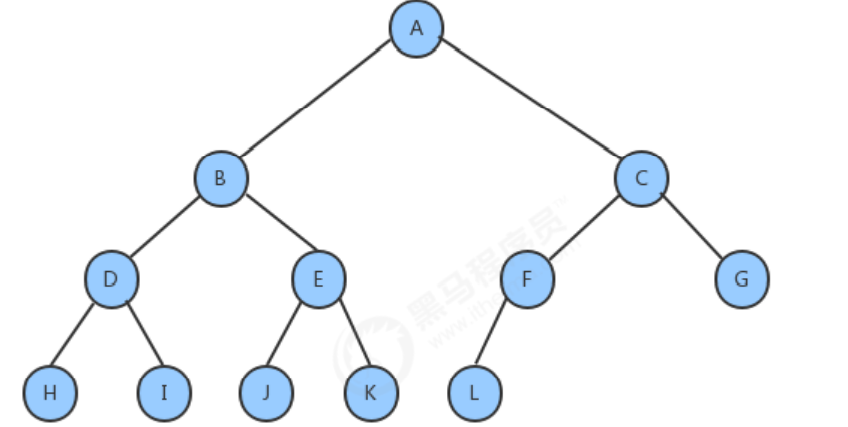
完全二叉树:
叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树
1.4 二叉查找树的创建
1.4.1二叉树的结点类
根据对图的观察,我们发现二叉树其实就是由一个一个的结点及其之间的关系组成的,按照面向对象的思想,我们设计一个结点类来描述结点这个事物。
结点类API设计:

代码实现:
private class Node<Key,Value>{
//存储键
public Key key;
//存储值
private Value value;
//记录左子结点
public Node left;
//记录右子结点
public Node right;
public Node(Key key, Value value, Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
1.4.2 二叉查找树API设计

1.4.3 二叉查找树实现
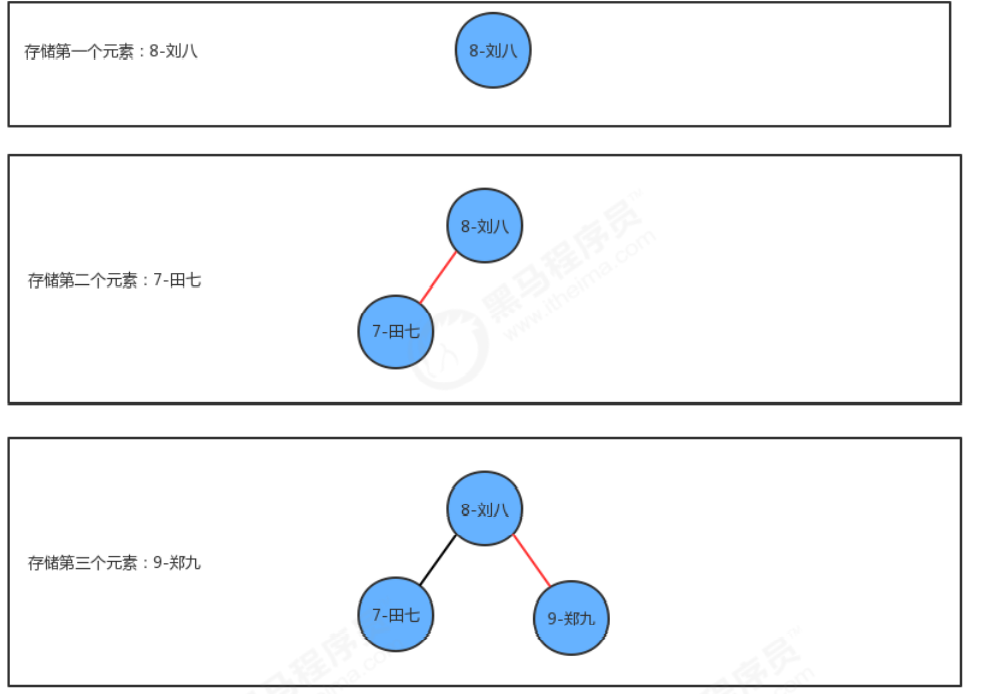
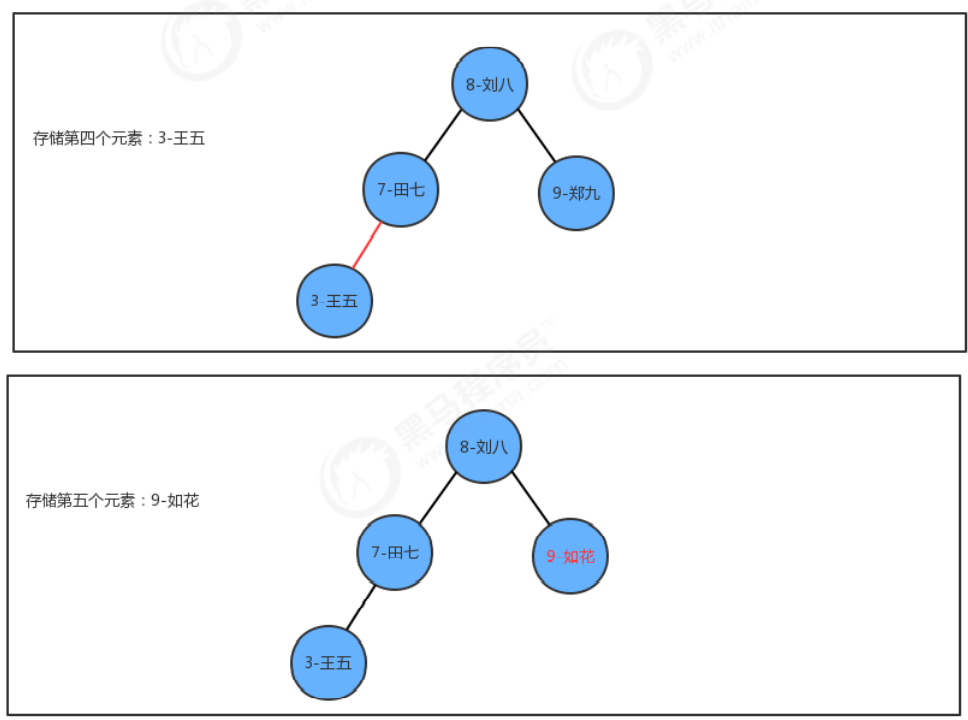
插入方法put实现思想:
- 如果当前树中没有任何一个结点,则直接把新结点当做根结点使用
- 如果当前树不为空,则从根结点开始:
2.1 如果新结点的key小于当前结点的key,则继续找当前结点的左子结点;
2.2 如果新结点的key大于当前结点的key,则继续找当前结点的右子结点;
2.3 如果新结点的key等于当前结点的key,则树中已经存在这样的结点,替换该结点的value值即可。
查询方法get实现思想:
从根节点开始:
- 如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;
- 如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;
- 如果要查询的key等于当前结点的key,则树中返回当前结点的value。
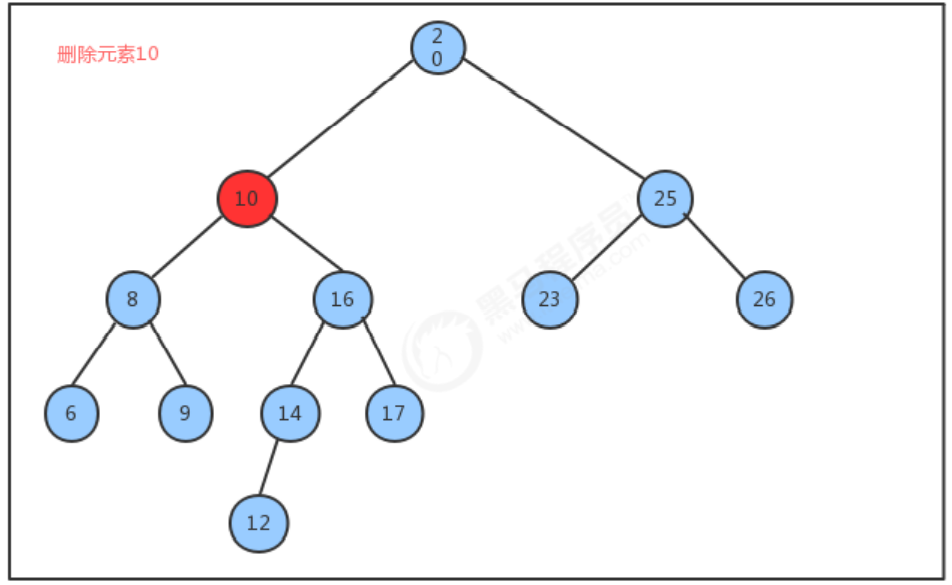
删除方法delete实现思想:
- 找到被删除结点;
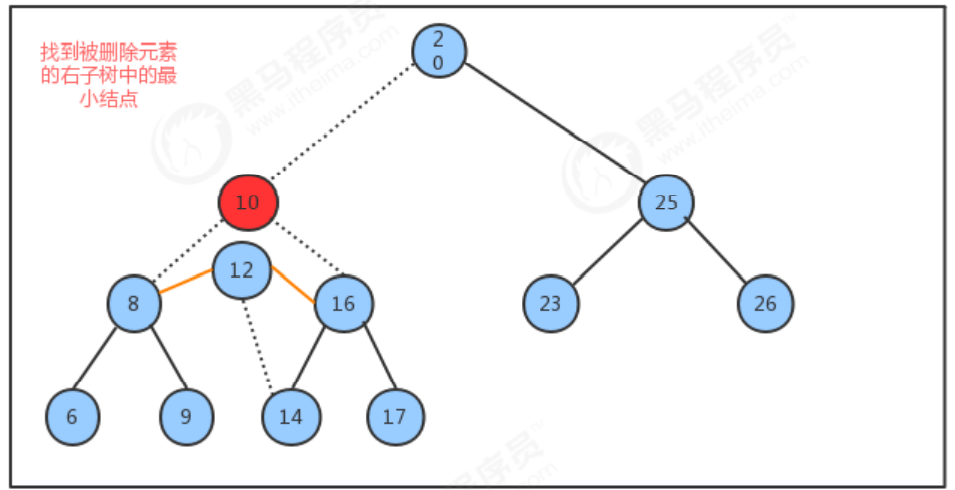
- 找到被删除结点右子树中的最小结点minNode
- 删除右子树中的最小结点
- 让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点minNode的右子树
- 让被删除结点的父节点指向最小结点minNode

代码:
//二叉树代码
public class BinaryTree<Key extends Comparable<Key>, Value> {
//记录根结点
private Node root;
//记录树中元素的个数
private int N;
//获取树中元素的个数
public int size() {
return N;
}
//向树中添加元素key-value
public void put(Key key, Value value) {
root = put(root, key, value);
}
//向指定的树x中添加key-value,并返回添加元素后新的树
private Node put(Node x, Key key, Value value) {
if (x == null) {
//个数+1
N++;
return new Node(key, value, null, null);
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//新结点的key大于当前结点的key,继续找当前结点的右子结点
x.right = put(x.right, key, value);
} else if (cmp < 0) {
//新结点的key小于当前结点的key,继续找当前结点的左子结点
x.left = put(x.left, key, value);
} else {
//新结点的key等于当前结点的key,把当前结点的value进行替换
x.value = value;
}
return x;
}
//查询树中指定key对应的value
public Value get(Key key) {
return get(root, key);
}
//从指定的树x中,查找key对应的值
public Value get(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//如果要查询的key大于当前结点的key,则继续找当前结点的右子结点;
return get(x.right, key);
} else if (cmp < 0) {
//如果要查询的key小于当前结点的key,则继续找当前结点的左子结点;
return get(x.left, key);
} else {
//如果要查询的key等于当前结点的key,则树中返回当前结点的value。
return x.value;
}
}
//删除树中key对应的value
public void delete(Key key) {
root = delete(root, key);
}
//删除指定树x中的key对应的value,并返回删除后的新树
public Node delete(Node x, Key key) {
if (x == null) {
return null;
}
int cmp = key.compareTo(x.key);
if (cmp > 0) {
//新结点的key大于当前结点的key,继续找当前结点的右子结点
x.right = delete(x.right, key);
} else if (cmp < 0) {
//新结点的key小于当前结点的key,继续找当前结点的左子结点
x.left = delete(x.left, key);
} else {
//新结点的key等于当前结点的key,当前x就是要删除的结点
//1.如果当前结点的右子树不存在,则直接返回当前结点的左子结点
if (x.right == null) {
return x.left;
}
//2.如果当前结点的左子树不存在,则直接返回当前结点的右子结点
if (x.left == null) {
return x.right;
}
//3.当前结点的左右子树都存在
//3.1找到右子树中最小的结点
Node minNode = x.right;
while (minNode.left != null) {
minNode = minNode.left;
}
//3.2删除右子树中最小的结点
Node n = x.right;
while (n.left != null) {
if (n.left.left == null) {
n.left = null;
} else {
n = n.left;
}
}
//3.3让被删除结点的左子树称为最小结点minNode的左子树,让被删除结点的右子树称为最小结点
minNode的右子树
minNode.left = x.left;
minNode.right = x.right;
//3.4让被删除结点的父节点指向最小结点minNode
x = minNode;
//个数-1
N--;
}
return x;
}
private class Node {
//存储键
public Key key;
//存储值
private Value value;
//记录左子结点
public Node left;
//记录右子结点
public Node right;
public Node(Key key, Value value, Node left, Node right) {
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<Integer, String> bt = new BinaryTree<>();
bt.put(4, "二哈");
bt.put(1, "张三");
bt.put(3, "李四");
bt.put(5, "王五");
System.out.println(bt.size());
bt.put(1,"老三");
System.out.println(bt.get(1));
System.out.println(bt.size());
bt.delete(1);
System.out.println(bt.size());
}
}
1.4.4 二叉查找树其他便捷方法
1.4.4.1 查找二叉树中最小的键
在某些情况下,我们需要查找出树中存储所有元素的键的最小值,比如我们的树中存储的是学生的排名和姓名数据,那么需要查找出排名最低是多少名?这里我们设计如下两个方法来完成:

//找出整个树中最小的键
public Key min(){
return min(root).key;
}
//找出指定树x中最小的键所在的结点
private Node min(Node x){
if (x.left!=null){
return min(x.left);
}else{
return x;
}
}
1.4.4.2 查找二叉树中最大的键
在某些情况下,我们需要查找出树中存储所有元素的键的最大值,比如我们的树中存储的是学生的成绩和学生的姓名,那么需要查找出最高的分数是多少?这里我们同样设计两个方法来完成:

//找出整个树中最大的键
public Key max(){
return max(root).key;
}
//找出指定树x中最大键所在的结点
public Node max(Node x){
if (x.right!=null){
return max(x.right);
}else{
return x;
}
}
1.5 二叉树的基础遍历
很多情况下,我们可能需要像遍历数组数组一样,遍历树,从而拿出树中存储的每一个元素,由于树状结构和线性结构不一样,它没有办法从头开始依次向后遍历,所以存在如何遍历,也就是按照什么样的搜索路径进行遍历的问题。
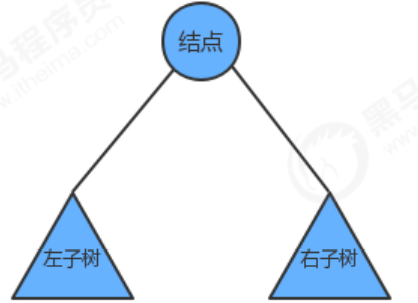
我们把树简单的画作上图中的样子,由一个根节点、一个左子树、一个右子树组成,那么按照根节点什么时候被访问,我们可以把二叉树的遍历分为以下三种方式:
- 前序遍历;
先访问根结点,然后再访问左子树,最后访问右子树 - 中序遍历;
先访问左子树,中间访问根节点,最后访问右子树 - 后序遍历;
先访问左子树,再访问右子树,最后访问根节点
如果我们分别对下面的树使用三种遍历方式进行遍历,得到的结果如下:
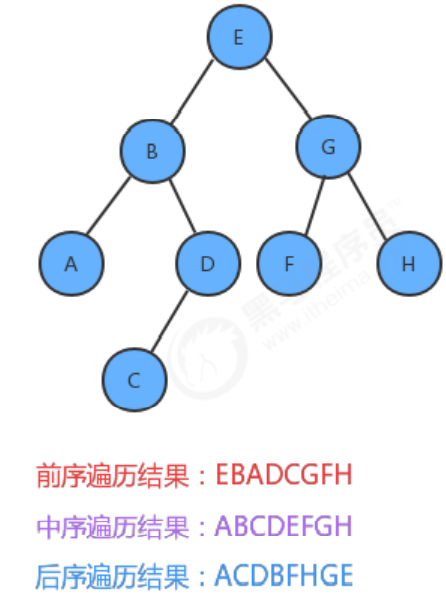
1.5.1 前序遍历
我们在4.4中创建的树上,添加前序遍历的API:
public Queue<Key> preErgodic():使用前序遍历,获取整个树中的所有键
private void preErgodic(Node x,Queue<Key> keys):使用前序遍历,把指定树x中的所有键放入到keys队列中
实现过程中,我们通过前序遍历,把,把每个结点的键取出,放入到队列中返回即可。
实现步骤:
- 把当前结点的key放入到队列中;
- 找到当前结点的左子树,如果不为空,递归遍历左子树
- 找到当前结点的右子树,如果不为空,递归遍历右子树
代码:
//使用前序遍历,获取整个树中的所有键
public Queue<Key> preErgodic(){
Queue<Key> keys = new Queue<>();
preErgodic(root,keys);
return keys;
}
//使用前序遍历,把指定树x中的所有键放入到keys队列中
private void preErgodic(Node x,Queue<Key> keys){
if (x==null){
return;
}
//1.把当前结点的key放入到队列中;
keys.enqueue(x.key);
//2.找到当前结点的左子树,如果不为空,递归遍历左子树
if (x.left!=null){
preErgodic(x.left,keys);
}
//3.找到当前结点的右子树,如果不为空,递归遍历右子树
if (x.right!=null){
preErgodic(x.right,keys);
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<String, String> bt = new BinaryTree<>();
bt.put("E", "5");
bt.put("B", "2");
bt.put("G", "7");
bt.put("A", "1");
bt.put("D", "4");
bt.put("F", "6");
bt.put("H", "8");
bt.put("C", "3");
Queue<String> queue = bt.preErgodic();
for (String key : queue) {
System.out.println(key+"="+bt.get(key));
}
}
}
1.5.2 中序遍历
我们在1.4中创建的树上,添加前序遍历的API:
public Queue<Key> midErgodic():使用中序遍历,获取整个树中的所有键
private void midErgodic(Node x,Queue<Key> keys):使用中序遍历,把指定树x中的所有键放入到keys队列中
实现步骤:
- 找到当前结点的左子树,如果不为空,递归遍历左子树
- 把当前结点的key放入到队列中;
- 找到当前结点的右子树,如果不为空,递归遍历右子树
代码:
//使用中序遍历,获取整个树中的所有键
public Queue<Key> midErgodic(){
Queue<Key> keys = new Queue<>();
midErgodic(root,keys);
return keys;
}
//使用中序遍历,把指定树x中的所有键放入到keys队列中
private void midErgodic(Node x,Queue<Key> keys){
if (x==null){
return;
}
//1.找到当前结点的左子树,如果不为空,递归遍历左子树
if (x.left!=null){
midErgodic(x.left,keys);
}
//2.把当前结点的key放入到队列中;
keys.enqueue(x.key);
//3.找到当前结点的右子树,如果不为空,递归遍历右子树
if (x.right!=null){
midErgodic(x.right,keys);
}
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<String, String> bt = new BinaryTree<>();
bt.put("E", "5");
bt.put("B", "2");
bt.put("G", "7");
bt.put("A", "1");
bt.put("D", "4");
bt.put("F", "6");
bt.put("H", "8");
bt.put("C", "3");
Queue<String> queue = bt.midErgodic();
for (String key : queue) {
System.out.println(key+"="+bt.get(key));
}
}
}
1.5.3 后序遍历
我们在1.4中创建的树上,添加前序遍历的API:
public Queue<Key> afterErgodic():使用后序遍历,获取整个树中的所有键
private void afterErgodic(Node x,Queue<Key> keys):使用后序遍历,把指定树x中的所有键放入到keys队列中
实现步骤:
- 找到当前结点的左子树,如果不为空,递归遍历左子树
- 找到当前结点的右子树,如果不为空,递归遍历右子树
- 把当前结点的key放入到队列中;
代码
//使用后序遍历,获取整个树中的所有键
public Queue<Key> afterErgodic(){
Queue<Key> keys = new Queue<>();
afterErgodic(root,keys);
return keys;
}
//使用后序遍历,把指定树x中的所有键放入到keys队列中
private void afterErgodic(Node x,Queue<Key> keys){
if (x==null){
return;
}
//1.找到当前结点的左子树,如果不为空,递归遍历左子树
if (x.left!=null){
afterErgodic(x.left,keys);
}
//2.找到当前结点的右子树,如果不为空,递归遍历右子树
if (x.right!=null){
afterErgodic(x.right,keys);
}
//3.把当前结点的key放入到队列中;
keys.enqueue(x.key);
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<String, String> bt = new BinaryTree<>();
bt.put("E", "5");
bt.put("B", "2");
bt.put("G", "7");
bt.put("A", "1");
bt.put("D", "4");
bt.put("F", "6");
bt.put("H", "8");
bt.put("C", "3");
Queue<String> queue = bt.afterErgodic();
for (String key : queue) {
System.out.println(key+"="+bt.get(key));
}
}
}
1.6 二叉树的层序遍历
所谓的层序遍历,就是从根节点(第一层)开始,依次向下,获取每一层所有结点的值,有二叉树如下:
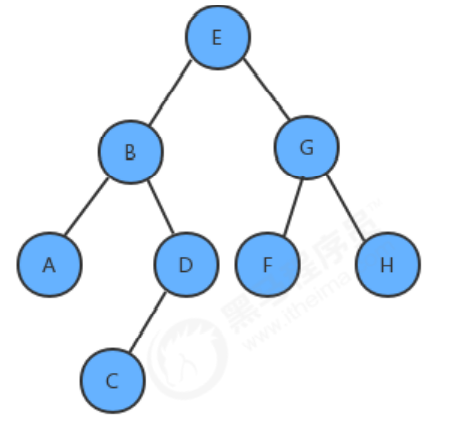
那么层序遍历的结果是:EBGADFHC
我们在4.4中创建的树上,添加层序遍历的API:
public Queue<Key> layerErgodic():使用层序遍历,获取整个树中的所有键
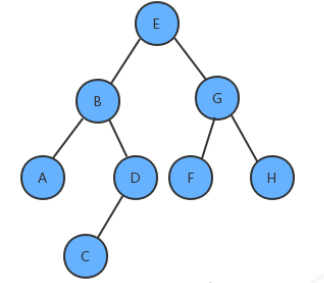
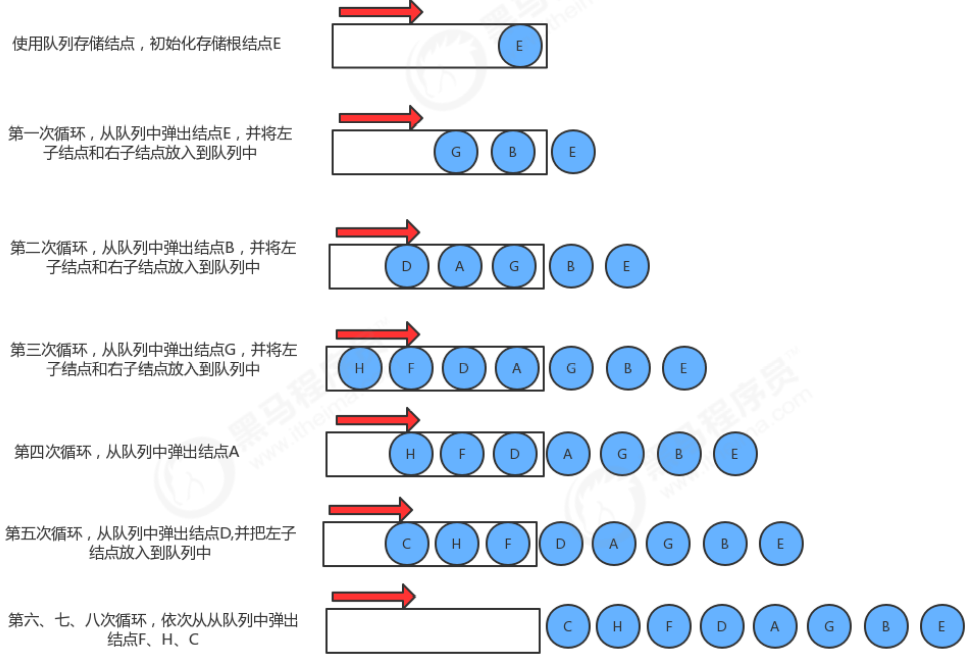
实现步骤:
- 创建队列,存储每一层的结点;
- 使用循环从队列中弹出一个结点:
2.1 获取当前结点的key;
2.2 如果当前结点的左子结点不为空,则把左子结点放入到队列中
2.3 如果当前结点的右子结点不为空,则把右子结点放入到队列中
代码
//使用层序遍历得到树中所有的键
public Queue<Key> layerErgodic(){
Queue<Key> keys = new Queue<>();
Queue<Node> nodes = new Queue<>();
nodes.enqueue(root);
while(!nodes.isEmpty()){
Node x = nodes.dequeue();
keys.enqueue(x.key);
if (x.left!=null){
nodes.enqueue(x.left);
}
if (x.right!=null){
nodes.enqueue(x.right);
}
}
return keys;
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<String, String> bt = new BinaryTree<>();
bt.put("E", "5");
bt.put("B", "2");
bt.put("G", "7");
bt.put("A", "1");
bt.put("D", "4");
bt.put("F", "6");
bt.put("H", "8");
bt.put("C", "3");
Queue<String> queue = bt.layerErgodic();
for (String key : queue) {
System.out.println(key+"="+bt.get(key));
}
}
}
1.7 二叉树的最大深度问题
需求:
给定一棵树,请计算树的最大深度(树的根节点到最远叶子结点的最长路径上的结点数)
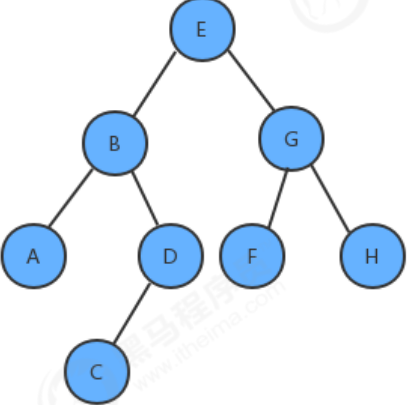
上面这棵树的最大深度为4。
实现:
我们在1.4中创建的树上,添加如下的API求最大深度:
public int maxDepth():计算整个树的最大深度
private int maxDepth(Node x):计算指定树x的最大深度
实现步骤:
- 如果根结点为空,则最大深度为0;
- 计算左子树的最大深度;
- 计算右子树的最大深度;
- 当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1
代码:
//计算整个树的最大深度
public int maxDepth() {
return maxDepth(root);
}
//计算指定树x的最大深度
private int maxDepth(Node x) {
//1.如果根结点为空,则最大深度为0;
if (x == null) {
return 0;
}
int max = 0;
int maxL = 0;
int maxR = 0;
//2.计算左子树的最大深度;
if (x.left != null) {
maxL = maxDepth(x.left);
}
//3.计算右子树的最大深度;
if (x.right != null) {
maxR = maxDepth(x.right);
}
//4.当前树的最大深度=左子树的最大深度和右子树的最大深度中的较大者+1
max = maxL > maxR ? maxL + 1 : maxR + 1;
return max;
}
//测试代码
public class Test {
public static void main(String[] args) throws Exception {
BinaryTree<String, String> bt = new BinaryTree<>();
bt.put("E", "5");
bt.put("B", "2");
bt.put("G", "7");
bt.put("A", "1");
bt.put("D", "4");
bt.put("F", "6");
bt.put("H", "8");
bt.put("C", "3");
int i = bt.maxDepth();
System.out.println(i);
}
}
1.8 折纸问题
需求:
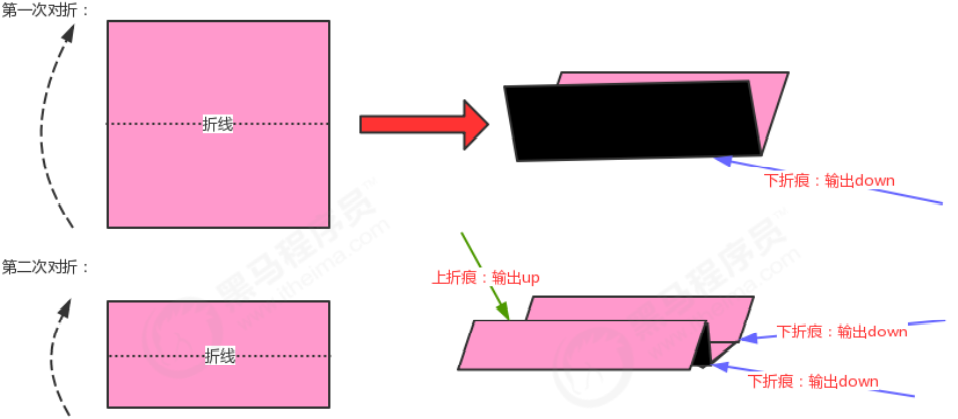
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时 折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2 次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一 个输入参数N,代表纸条都从下边向上方连续对折N次,请从上到下打印所有折痕的方向 例如:N=1时,打印: down;N=2时,打印: down down up
分析:
我们把对折后的纸张翻过来,让粉色朝下,这时把第一次对折产生的折痕看做是根结点,那第二次对折产生的下折痕就是该结点的左子结点,而第二次对折产生的上折痕就是该结点的右子结点,这样我们就可以使用树型数据结构来描述对折后产生的折痕。
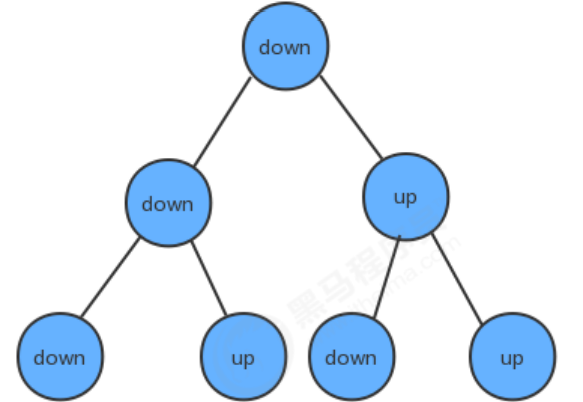
这棵树有这样的特点:
- 根结点为下折痕;
- 每一个结点的左子结点为下折痕;
- 每一个结点的右子结点为上折痕;
实现步骤:
- 定义结点类
- 构建深度为N的折痕树;
- 使用中序遍历,打印出树中所有结点的内容;
构建深度为N的折痕树:
- 第一次对折,只有一条折痕,创建根结点;
- 如果不是第一次对折,则使用队列保存根结点;
- 循环遍历队列:
3.1 从队列中拿出一个结点;
3.2 如果这个结点的左子结点不为空,则把这个左子结点添加到队列中;
3.3 如果这个结点的右子结点不为空,则把这个右子结点添加到队列中;
3.4 判断当前结点的左子结点和右子结点都不为空,如果是,则需要为当前结点创建一个值为down的左子结点,一个值为up的右子结点。
代码:
public class PaperFolding {
public static void main(String[] args) {
//构建折痕树
Node tree = createTree(3);
//遍历折痕树,并打印
printTree(tree);
}
//3.使用中序遍历,打印出树中所有结点的内容;
private static void printTree(Node tree) {
if (tree==null){
return;
}
printTree(tree.left);
System.out.print(tree.item+",");
printTree(tree.right);
}
//2.构建深度为N的折痕树;
private static Node createTree(int N) {
Node root = null;
for (int i = 0; i <N ; i++) {
if (i==0){
//1.第一次对折,只有一条折痕,创建根结点;
root = new Node("down",null,null);
}else{
//2.如果不是第一次对折,则使用队列保存根结点;
Queue<Node> queue = new Queue<>();
queue.enqueue(root);
//3.循环遍历队列:
while(!queue.isEmpty()){
//3.1从队列中拿出一个结点;
Node tmp = queue.dequeue();
//3.2如果这个结点的左子结点不为空,则把这个左子结点添加到队列中;
if (tmp.left!=null){
queue.enqueue(tmp.left);
}
//3.3如果这个结点的右子结点不为空,则把这个右子结点添加到队列中;
if (tmp.right!=null){
queue.enqueue(tmp.right);
}
//3.4判断当前结点的左子结点和右子结点都不为空,如果是,则需要为当前结点创建一个值为down的左子结点,一个值为up的右子结点。
if (tmp.left==null && tmp.right==null){
tmp.left = new Node("down",null,null);
tmp.right = new Node("up",null,null);
}
}
}
}
return root;
}
//1.定义结点类
private static class Node{
//存储结点元素
String item;
//左子结点
Node left;
//右子结点
Node right;
//结点类
private static class Node<T>{
public T item;//存储元素
public Node left;
public Node right;
public Node(T item, Node left, Node right) {
this.item = item;
this.left = left;
this.right = right;
}
}
}