试题E：蜂巢

解析

很明显的一道坐标计算问题，只是通过看似比较复杂的描述而已。
题目定义了一种行走方向，大概就是一共六种行走方向，如果以o为原点，建立坐标系，那么方向0和3就是x轴。其他方向为分力即可，如1就是(-0.5,0.5)，2就是(0.5,0.5)，然后计算步数就好了。

• 模拟行走路径，然后拆分为我们定义的坐标
• 通过两点坐标，计算步数
  $$f(w,x,y,z)=abs(w-x)+abs(y-z)$$

证明：
对于正六边形而言，每个夹角都为120°，那么如图：

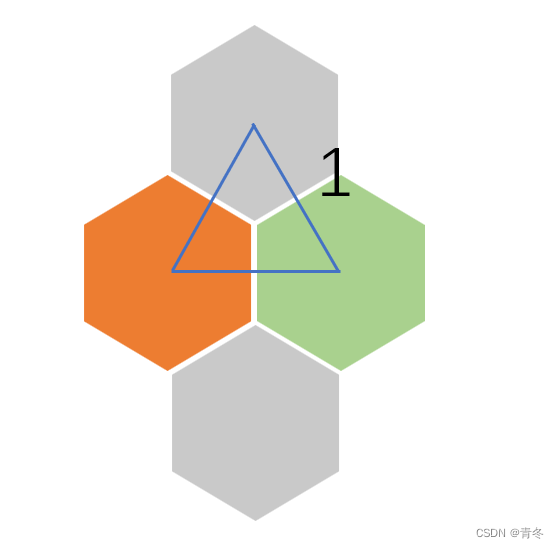
连接三个正六边形中心的线段长都一样并且设为1则边际线切分为两半为0.5，刚好距离计算从黄到灰为0.5+0.5=1 。

代码

package com.maggot.maggotscheduler.bootstrap.utils.lanqiaobei13;

/**
 * @author huangyichun
 */
public class E蜂巢 {
    public static void main(String[] args) {
        XY B = getxy(0, 5, 3);
        XY C = getxy(2, 3, 2);
        System.out.println(B);
        System.out.println(C);
        System.out.println("B.getFarFrom(C) = " + B.getFarFrom(C));
    }


    public static XY getxy(int d, double p, double q) {
        switch (d) {
            case 0:
                return new XY(-p + q / 2, 0 + q / 2);
            case 1:
                return new XY(-p / 2 + q, p / 2);
            case 2:
                return new XY(p / 2 + q / 2, p / 2 - q / 2);
            case 3:
                return new XY(p - q / 2, 0 - q / 2);
            case 4:
                return new XY(p / 2 - q, -p / 2);
            case 5:
                return new XY(-p / 2 - q / 2, -p / 2 + q / 2);
            default:
                return new XY(0, 0);
        }
    }


    private static class XY {
        double x;
        double y;

        public XY(double x, double y) {
            this.x = x;
            this.y = y;
        }

        public double getFarFrom(XY other) {
            return Math.abs(x - other.x) + Math.abs(y - other.y);
        }

        @Override
        public String toString() {
            return "XY{" +
                    "x=" + x +
                    ", y=" + y +
                    '}';
        }
    }
}