---

前言

约数和质数一样在蓝桥杯考试中是在数论中考察频率较高的一种，在省赛考察的时候往往就是模板题，难度大一点会结合其他知识点考察，但是仍然会用到模板，这里有三大模板，第一个是试除法求约数个数，第二个是求约数个数，第三个是求约数的和(来自y总的三个模型）

---

一、约数是什么

约数(约数的含义是什么) 1、意思 1.大约的数目。 2.一个数能够整除另一数，这个数就是另一数的约数。如2，3，4，6都能整除12，因此2，3，4，6都是12的约数。也叫因数。最后俩个都插到这个动态数组中，但是注意

---

二、三大模板

1、试除法求约数个数

算法思想：算x的约数，对 小于等于x的根号数求约数，当你求得一个约数，对应的也有另一个数是约数，就比如算12的约数，当算出3是约数,可得 4（12/ 3）也是12的约数。但是注意如果16的约数4对应的约数还是4不能在被放进去，所以要加一个特判

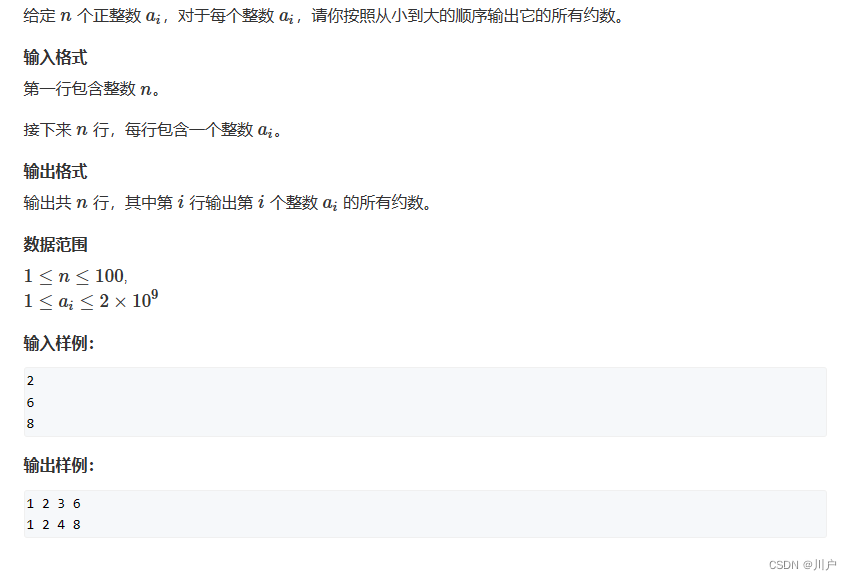
代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> get_divisors(int n)
{
    vector <int> res;
    for(int i = 1;i <= n / i; i ++)
    {
        if(n % i == 0){
            res.push_back(i);
            if(i != n / i) res.push_back(n/i);
        }
    }
    sort(res.begin(),res.end());
    return res;
}
int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int x;
        cin >> x;
        vector <int> res;
        res = get_divisors(x);
        for(auto c : res)
        {
            cout << c << " ";
        }
        cout << endl;
            
    
    }
}

2、求约数个数

如果有一个数n，且 n = p1^c1 * p2 ^ c2 * p3 ^c3 + ...... + pn^cn;

那么它的约数个数和就等于 (c1 + 1 ) * ( c2 + 1 ) * (c3 + 1 ) ....(cn + 1);

p1^c1,这样的数就是上文中所介绍的质因数，通过求质因数，在求c1 + 1的值即可。

题目·

 代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
const int mod = 1e9 + 7;
typedef long long LL;
using namespace std;
int main()
{
    unordered_map <int,int> primes;
    int n;
    cin >> n;
    while (n -- )
    {
        int x;
        cin >> x;
        for(int i = 2;i <= x / i;i ++)
        {
            while(x % i == 0)
            {
                x /= i;
                primes[i] ++;
            }
            
        }
        if(x > 1) primes[x] ++;
    }
    
    LL res = 1;
    for(auto c: primes)
    {
        res  = res * (c.second + 1) % mod;
    }
    cout << res << endl;
}

3、求约数之和

如果有一个数n，且 n = p1^c1 * p2 ^ c2 * p3 ^c3 + ...... + pn^cn;

那么它的约数之和为（p1^0  + p2^1 + p3 ^3 + .. +p^c1） * ... *( pn^c1 + pn^c2 +pn^c3  + ...+ pn^cn)

求解方法和上面一样，先是解出质因数，然后求出约数和的过程很巧妙，看下面代码

题目

 

题解

#include <bits/stdc++.h>
typedef long long LL;
const int mod = 1e9 + 7;
using namespace std;
int main()
{
    unordered_map<int,int> primes;   //一个值存的是这个质因数，第二个存的是指数
    int n;
    cin >>n;
    while (n -- )
    {
        int x;
        cin >> x;
        for(int i = 2;i <= x / i;i ++)
        {
            while(x % i == 0) 
            {
               x /= i;
               primes[i] ++ ;   // 指数加一
            }
        
        }
        if(x > 1) primes[x] ++;
    }
    LL res = 1;
    for(auto c : primes)
    {
        int a = c.first,b = c.second;
        LL t = 1;
        while(b--)  t = (t * a + 1) % mod;
        res = res * t % mod;
    }
    cout << res << endl;
}

最后一步为什么会用这个t ，假设开始时为 

t : 1   

t :p+ 1 （t = 1 *p + 1）

t : p^2 + p  +1 ( t = (p+1) * p +1 )\

....

最后t : t=p^b+p^b−1+…+1

 

四、求最大公约数

求最大公约数，要用到欧几里得算法，就是 gcd (a,b) = gcd(b,a%b），注意b为0的时候按照欧几里得算法，b等于0，取a；

题目

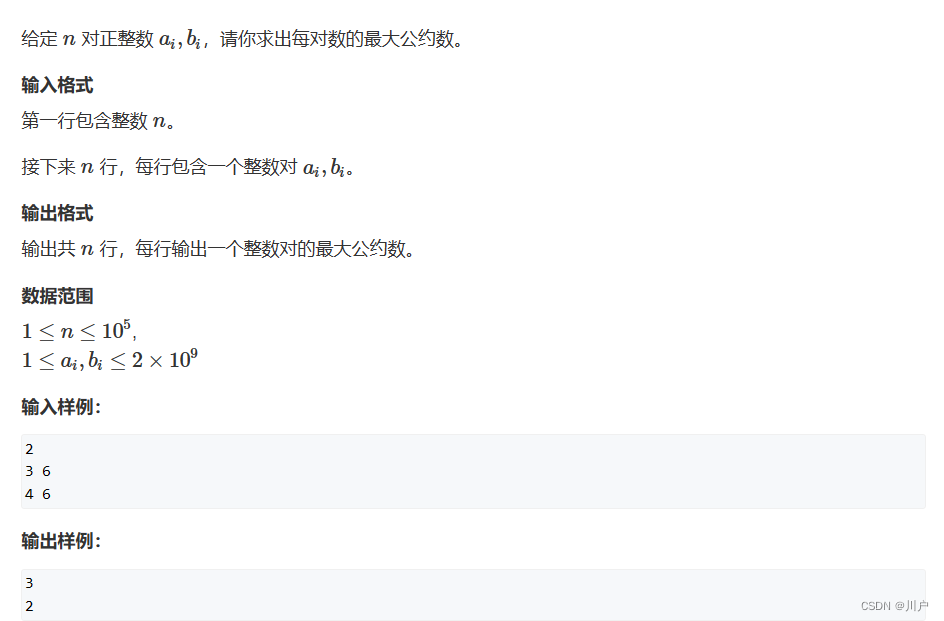
 代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
int gcd(int a,int b)
{
    return b ? gcd(b,a%b):a ;  //b为0的时候按照欧几里得算法，b等于0，取a
}

int main()
{
    int n;
    cin >> n;
    while(n --)
    {
        int a,b;
        cin >> a >> b;
        int t =gcd(a,b);
        cout << t <<endl;
    }
}

 

---

 

三、真题演练

2020填空题

题目

题目描述

本题为填空题，只需要算出结果后，在代码中使用输出语句将所填结果输出即可。

12000001200000 有多少个约数（只计算正约数）。

运行限制

• 最大运行时间：1s
• 最大运行内存: 128M

代码

#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_map>
const int mod = 1e9 + 7;
typedef long long LL;
using namespace std;
int main()
{
    unordered_map <int,int> primes;
 
    int x;
    x = 1200000;
    for(int i = 2;i <= x / i;i ++)
    {
        while(x % i == 0)
        {
            x /= i;
            primes[i] ++;
        }
            
    }
    if(x > 1) primes[x] ++;

    LL res = 1;
    for(auto c: primes)
    {
        res  = res * (c.second + 1) % mod;
    }
    cout << res << endl;
}