2023.3.13~4.13持续更新

目录

🍎注意

🌼前言

🌼十，KMP（留坑）

🌼十一，Trie（留坑）

🌼十二，BFS

👊(一)1562. 微博转发

🌳AC  BFS暴力 + queue + stack(未完成)

🌳AC  Floyd-Warshall暴力

👊（二）机器人的运动范围

🌳BFS  AC  40%

🌳BFS  AC  75%

🌳BFS  AC  100%

🌳DFS  AC  100%

👊（三）188. 武士风度的牛

👊（四）P1451 求细胞数量

🌳暴力BFS

🌳暴力DFS

👊（五）1810: [NewOJ Week 4] 超级骑士

🌳广搜  AC

🌳深搜  AC

🌼十三，

🌼十四，

🌼十五，Dijkstra

🌼十六，

🌼十七，

🌼十八，

🌼十九，

🌼二十，

🍋总结 

---

🍎注意

上篇博客写完第8个题型已经32747字了，卡得写不动了，敲完一行字等10秒才显示

每10个题型写一个博客，分为上中下三个博客，12万字收尾

后续再补充剩下两个博客地址

(上)(1条消息) 30个题型+代码(冲刺2023蓝桥杯)(上)_码龄?天的博客-CSDN博客

🌼前言

前缀和√，差分√，二分√，双指针√，递归√，递推√，BFS√，DFS，Dijkstra, Floyd，质数筛，最大公约数，背包dp，线性dp，区间dp，组合计数，快速幂，哈希√，并查集√，博弈论 

每个类型第一题来自AcWing蓝桥杯集训-每日一题

1，花5块钱

2，上洛谷找替代 / 原题 

题型有

前缀和，差分，二分，双指针，递推，递归，并查集，哈希，单调队列，
KMP，Trie，BFS，DFS，拓扑排序，Dijkstra，Floyd，最小生成树，
最近公共祖先，二分图，筛质数，最大公约数，快速幂，组合计数，博弈论，
背包DP，线性DP，区间DP，树型DP，树状数组，线段树，矩阵乘法 

如果你想冲省一，拿22年A组为例，你得拿60分，也就是2道填空题 + 4道编程题

5 + 5 + 10 + 10 + 15 + 15

省赛需要掌握的有：

前缀和，差分，二分，双指针，递归，递推，BFS，DFS，Dijkstra, Floyd，质数筛，最大公约数，背包dp，线性dp，区间dp，组合计数，快速幂，哈希，并查集，博弈论

围绕省赛需要掌握的类型，针对性地下手

先给大家看个时间复杂度（来源于AcWing）

🌼十，KMP（留坑）

👂 Secret Base (吉他版)（未闻花名(绝美指弹吉他)） - uBio高尾和树 - 单曲 - 网易云音乐 

→ KMP算法笔记 - AcWing

→ KMP 算法详解 - AcWing

→ 字符串匹配 - OI Wiki (oi-wiki.org)

→ 前缀函数与 KMP 算法 - OI Wiki (oi-wiki.org)

→ KMP算法详解-彻底清楚了(转载+部分原创) - sofu6 - 博客园 (cnblogs.com)

→ KMP算法详解_小轩爱学习的博客-CSDN博客

→ KMP 算法详解 - 知乎 (zhihu.com)

→ 数据结构KMP算法配图详解（超详细）_kmp算法图解_哈顿之光的博客-CSDN博客

🌼十一，Trie（留坑）

👂 想去海边 - 夏日入侵企画 - 单曲 - 网易云音乐

🌼十二，BFS

👂 逝年 - 夏小虎 - 单曲 - 网易云音乐

👇BFS科普博客

→ 《啊哈算法第四章之bfs》（17张图解）_码龄?天的博客-CSDN博客

先将科普博客敲一遍

就是将迷宫按二维数组输入，0表示空地，1表示障碍物，输出起点到终点的步数

由于是一步一步扩展的，这个步数就是最短路

⚠ 只有边权为1，才能用用BFS求最短路

//迷宫2维数组里, 1障碍, 0未走过的空地, -1走过的空地
#include<cstdio> //scanf(), printf()
int a[51][51];
struct note
{
    int x, y, s; //横坐标,纵坐标,步数
};
int main()
{
    struct note que[2501]; //声明队列为结构体
    int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组

    int n, m; //n行m列
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i)
        for(int j = 1; j <= m; ++j)
            scanf("%d", &a[i][j]);

    int startx, starty, p, q; //起点终点坐标
    scanf("%d%d%d%d", &startx, &starty, &p, &q);

    //队列初始化
    int head = 1, tail = 1;
    //往队列插入迷宫入口坐标
    que[tail].x = startx;
    que[tail].y = starty;
    que[tail].s = 0; //入口步数为0
    tail++;
    a[startx][starty] = -1; //标记走过

    int flag = 0; //标记是否到达终点
    //当队列不为空
    int tx, ty; //临时变量
    while(head < tail) {
        //枚举四个方向
        for(int i = 0; i < 4; ++i) {
            tx = que[head].x + next[i][0];
            ty = que[head].y + next[i][1];
            //判断越界
            if(tx < 1 || ty < 1 || tx > n || ty > m)
                continue;
            //判断不为障碍且未走过
            if(a[tx][ty] == 0) {
                //bfs每个点只入队一次
                a[tx][ty] = -1;
                //新的点入队
                que[tail].x = tx;
                que[tail].y = ty;
                que[tail].s = que[head].s + 1; //上一步再+1
                tail++; //放最后
            }
            //到达终点
            if(tx == p && ty == q) {
                flag = 1;
                break;
            }
        }
        if(flag) break;
        head++; //继续后续点的扩展
    }
    //tail指向队尾下一位, 要-1
    printf("%d", que[tail - 1].s);
    return 0;
}

5 4
0 0 1 0
0 0 0 0
0 0 1 0
0 1 0 0
0 0 0 1
1 1 4 3
7

👇看动图 

→ 图文详解 DFS 算法 和 BFS 算法 - 墨天轮 (modb.pro)

→ 熬夜怒肝，图解算法！BFS和DFS的直观解释_Jack-Cui的博客-CSDN博客

👇bfs适用场景

→ 什么时候用DFS，什么时候用BFS? - 菜鸟龙* - 博客园 (cnblogs.com)

→ (1条消息) DFS和BFS应用场景（什么时候用）_bfs与dfs应用场景_binddddd的博客-CSDN博客

👊(一)1562. 微博转发

1562. 微博转发 - AcWing题库

标签：图论，BFS，中等，PAT甲级

 

思路

由样例可知，求最大转发量，就是求L层以内，关注这个用户的人数（不包括用户自己）

所以是有向图的多源最短路

嗯。。我不会邻接表，邻接矩阵和堆优化，所以只能暴力了，所幸这题数据量不大，暴力似乎也能过

🌳AC  BFS暴力 + queue + stack(未完成)

对每个点BFS一次

⚠ 只有边权为1，才能用用BFS求最短路

1，每个点要记录当前层数

2，同时用 st 数组判断是否访问过，防止重复入队

但是暴力bfs结合queue和stack，以减少代码量

bla...
//水一下，不会用Bfs做，先空着

🌳AC  Floyd-Warshall暴力

1，用一个二维数组存储图

2，Floyd，O(n^3)时间复杂度--暴力

3，最后要开O2优化

👇floyd科普博客（核心代码只有5行）

→ 最短路之Floyd-Warshall（10张图解）_码龄?天的博客-CSDN博客

再默写一遍floyd

#include<cstdio>
int e[10][10], k,i,j,n,m, t1,t2,t3, inf = 1e9;
int main()
{
    scanf("%d%d", &n, &m);
    //初始化地图
    for(i = 1; i <= n; ++i)
        for(j = 1; j <= n; ++j)
            if(i != j)
                e[i][j] = inf;
    //读入边
    for(i = 0; i < m; ++i) {
        scanf("%d%d%d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }
    //Floyd核心代码5行
    for(k = 1; k <= n; ++k)
        for(i = 1; i <= n; ++i)
            for(j = 1; j <= n; ++j)
                if(e[i][j] > e[i][k] + e[k][j])
                    e[i][j] = e[i][k] + e[k][j];
    //打印i到j的最短路
    for(i = 1; i <= n; ++i) {
        for(j = 1; j <= n; ++j)
            printf("   %d", e[i][j]);
        printf("\n");
    }
    return 0;
}

注意AC代码有个小坑，因为输入的第i组数据，表示i所关注的几个人，所以

代码第34行是 e[j][i] <= L，而不是 e[i][j] <= L

样例过了，再编一组测试

8 2
3 3 4 7
3 4 8 1
1 6
1 5
2 6 4
0
0
2 3 4
8 1 2 3 4 5 6 7 8
1
0
3
4
4
5
2
1

说下AC之前的2次错误吧

1，Segmentation Fault，内存超限，e[10][10] --> e[1010][1010]

2，Time Limit Exceeded，时间超限，可我寻思别人也能Floyd过，我咋不行

因为第一行没加#pragma GCC optimize(2)

这个是什么呢，类似洛谷的O2优化，而且蓝桥杯是支持的

它的好处是常数优化，卡极限AC，当然也有坏处

据说PAT不开O2优化能过，但是AcW不开就time limit

AC  代码

#pragma GCC optimize(2)
#include<cstdio>
int e[1010][1010], k,i,j,n,q, t1, inf = 1e9;
int main() //询问q次
{
    int L;
    scanf("%d%d", &n, &L);
    //初始化图
    for(i = 1; i <= n; ++i)
        for(j = 1; j <= n; ++j)
            if(i != j)
                e[i][j] = inf; //infinity无穷
    //读入边
    for(i = 1; i <= n; ++i) { //读入n次关注的人
        scanf("%d", &j); //关注j个人
        while(j) {
            j--;
            scanf("%d", &t1);
            e[i][t1] = 1; //顶点i到顶点t1距离为1
        }
    }
    //Floyd核心代码
    for(k = 1; k <= n; ++k)
        for(i = 1; i <= n; ++i)
            for(j = 1; j <= n; ++j)
                if(e[i][j] > e[i][k] + e[k][j])
                    e[i][j] = e[i][k] + e[k][j];
    //q次询问
    scanf("%d", &q);
    while(q) {
        q--;
        int ans = 0;
        scanf("%d", &i);
        for(int j = 1; j <= n; ++j)
            if(i != j && e[j][i] <= L) //注意是j指向i
                ans += 1;
        printf("%d\n", ans);
    }
    return 0;
}

所以说，Floyd的O(n^3)做这种数据量的题，也是有点勉强的，但放在蓝桥杯，数据量不太大的情况，足以骗到80%的分 

👊（二）机器人的运动范围

24. 机器人的运动范围 - AcWing题库

标签：BFS，DFS，简单，剑指offer

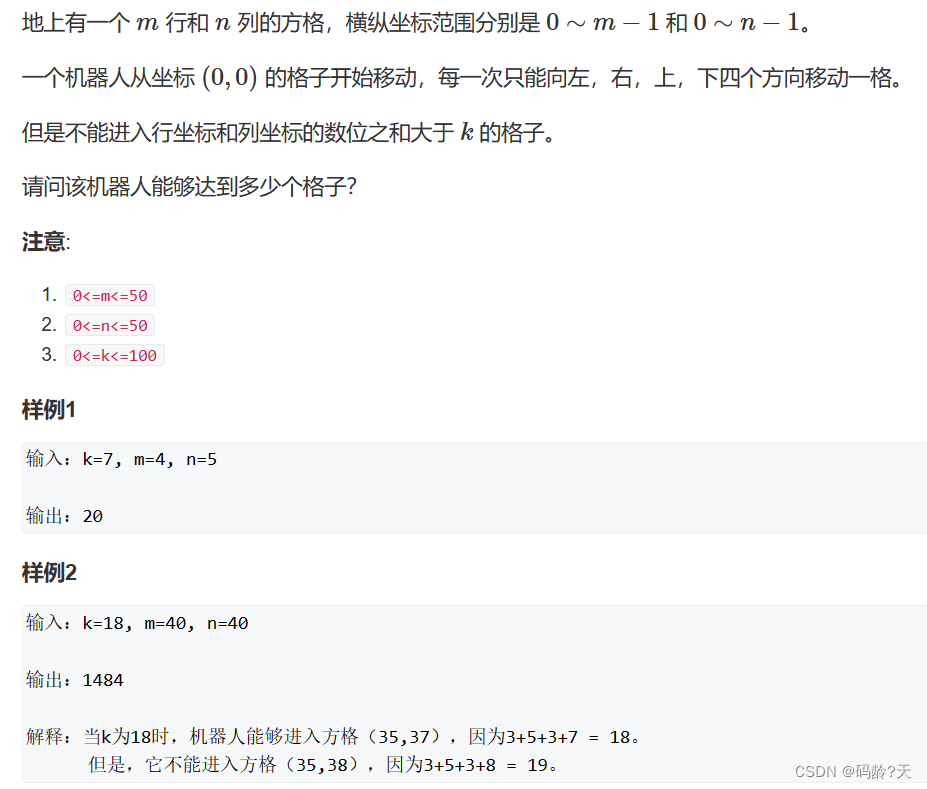
我一开始想，谁这么傻，不是两层暴力就出来了吗

🌳BFS  AC  40%

class Solution {
public:
    int get_num(int x, int y)
    {
        int s = 0;
        while(x) {
            s += x % 10;
            x /= 10;
        }
        while(y) {
            s += y % 10;
            y /= 10;
        }
        return s;
    }
    int movingCount(int threshold, int rows, int cols)
    {
        int ans = 0;
        for(int i = 0; i < rows; ++i)
            for(int j = 0; j < cols; ++j) {
                int now = get_num(i, j);
                if(now <= threshold)
                    ans += 1;
            }
        return ans;
    }
};

但我忽略了现实条件，有个真实不虚的机器人在移动，它是不可以飞的，而由于判断小于k的要求是，每一位相加判断（而不是两数相加），所以存在get_num(i, j) <= k但机器人无法到达的情况

所以还是得用BFS

🌳BFS  AC  75%

class Solution {
public:
    int getnum(int x, int y)
    {
        int s = 0;
        while(x) {
            s += x % 10;
            x /= 10;
        }
        while(y) {
            s += y % 10;
            y /= 10;
        }
        return s;
    }
    struct node
    {
        int x, y, s; //横坐标,纵坐标,路程
    };
    int movingCount(int k, int rows, int cols)
    {
        int book[51][51] = {0};
        struct node q[2510]; //队列扩展大于50*50即可
        //初始化队列
        int head = 0, tail = 0;
        q[tail].x = 0;
        q[tail].y = 0;
        q[tail].s = 1;
        tail++;
        book[0][0] = 1; //标记起点走过
        int tx, ty; //临时变量
        int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组
        //当队列不为空
        while(head < tail) {
            for(int i = 0; i < 4; ++i) {
                tx = q[head].x + next[i][0];
                ty = q[head].y + next[i][1];
                //判断边界
                if(tx < 0 || ty < 0 || tx >= rows || ty >= cols)
                    continue;
                //未到达过
                //此处if是所有bfs区别的地方
                if(book[tx][ty] == 0 && getnum(tx, ty) <= k) {
                    book[tx][ty] = 1;
                    q[tail].x = tx;
                    q[tail].y = ty;
                    q[tail].s = q[tail - 1].s + 1; //路程+1
                    tail++; //放最后
                }
            }
            head++; //继续其他点的扩展
        }
        return q[tail - 1].s; //tail指向队尾下一位, 要-1
    }
};

有个坑，如果行或列任一为0，说明方格不存在，只能输出0，最后需要分类讨论

🌳BFS  AC  100%

AcW代码

class Solution {
public:
    int getnum(int x, int y)
    {
        int s = 0;
        while(x) {
            s += x % 10;
            x /= 10;
        }
        while(y) {
            s += y % 10;
            y /= 10;
        }
        return s;
    }
    struct node
    {
        int x, y, s; //横坐标,纵坐标,路程
    };
    int movingCount(int k, int rows, int cols)
    {
        int book[51][51] = {0};
        struct node q[2510]; //队列扩展大于50*50即可
        //初始化队列
        int head = 0, tail = 0;
        q[tail].x = 0;
        q[tail].y = 0;
        q[tail].s = 1;
        tail++;
        book[0][0] = 1; //标记起点走过
        int tx, ty; //临时变量
        int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组
        //当队列不为空
        while(head < tail) {
            for(int i = 0; i < 4; ++i) {
                tx = q[head].x + next[i][0];
                ty = q[head].y + next[i][1];
                //判断边界
                if(tx < 0 || ty < 0 || tx >= rows || ty >= cols)
                    continue;
                //未到达过
                //此处if是所有bfs区别的地方
                if(book[tx][ty] == 0 && getnum(tx, ty) <= k) {
                    book[tx][ty] = 1;
                    q[tail].x = tx;
                    q[tail].y = ty;
                    q[tail].s = q[tail - 1].s + 1; //路程+1
                    tail++; //放最后
                }
            }
            head++; //继续其他点的扩展
        }
        if(rows == 0 || cols == 0)
            return 0;
        else
            return q[tail - 1].s; //tail指向队尾下一位, 要-1
    }
};

本地编译器代码

#include<iostream>
using namespace std;
int book[51][51];
struct node
{
    int x, y, s; //横坐标,纵坐标,路程
};
int getnum(int x, int y)
{
    int s = 0;
    while(x) {
        s += x % 10;
        x /= 10;
    }
    while(y) {
        s += y % 10;
        y /= 10;
    }
    return s;
}
int main()
{
    struct node q[2510]; //队列扩展大于50*50即可
    int k, rows, cols;
    cin>>k>>rows>>cols;
    //初始化队列
    int head = 0, tail = 0;
    q[tail].x = 0;
    q[tail].y = 0;
    q[tail].s = 1;
    tail++;
    book[0][0] = 1; //标记起点走过
    int tx, ty; //临时变量
    int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组
    //当队列不为空
    while(head < tail) {
        for(int i = 0; i < 4; ++i) {
            tx = q[head].x + next[i][0];
            ty = q[head].y + next[i][1];
            //判断边界
            if(tx < 0 || ty < 0 || tx >= rows || ty >= cols)
                continue;
            //未到达过
            //此处if是所有bfs区别的地方
            if(book[tx][ty] == 0 && getnum(tx, ty) <= k) {
                book[tx][ty] = 1;
                q[tail].x = tx;
                q[tail].y = ty;
                q[tail].s = q[tail - 1].s + 1; //路程+1
                tail++; //放最后
            }
        }
        head++; //继续其他点的扩展
    }
    if(rows == 0 || cols == 0)
        cout<<0;
    else
        cout<<q[tail - 1].s; //tail指向队尾下一位, 要-1
    return 0;
}

🌳DFS  AC  100%

貌似剑指offer还是可以声明全局变量，力扣不可以

尽管可以声明，给来的movingCount依旧是核心代码模式，所以

我给dfs函数整了5个参数

当然，据说可以

1，直接int dfs()，在函数里操作

2，通过取地址符传参

AcW代码

没有办法，只能给dfs整5个参数，取地址符不会用，dfs函数里直接操作也不会

class Solution {
public:
int book[51][51], vis[51][51], ans = 0;
int tx, ty;
    int getnum(int x, int y)
    {
        int s = 0;
        while(x) {
            s += x % 10;
            x /= 10;
        }
        while(y) {
            s += y % 10;
            y /= 10;
        }
        return s;
    }
    void dfs(int x, int y, int k, int rows, int cols)
    {
        int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
        //枚举4个方向
        for(int i = 0; i < 4; ++i) {
            //下一点坐标
            tx = x + next[i][0];
            ty = y + next[i][1];
            //超出范围
            if(tx < 0 || ty < 0 || tx >= rows || ty >= cols)
                continue;
            //没访问过且小于k
            if(book[tx][ty] == 0 && getnum(tx, ty) <= k) {
                book[tx][ty] = 1; //标记
                dfs(tx, ty, k, rows, cols); //递归
                book[tx][ty] = 0; //取消标记
            }
        }
        //切记, ans += 1的if判断放外面
        if(vis[x][y] == 0) {
            ans += 1;
            vis[x][y] = 1;
        }

    }
    int movingCount(int k, int rows, int cols)
    {
        book[0][0] = 1;
        dfs(0, 0, k, rows, cols);
        if(rows == 0 || cols == 0)
            return 0;
        else
            return ans;
    }
};

本地编译代码

#include<iostream>
using namespace std;
int book[51][51], vis[51][51], ans = 0;
int k, rows, cols, tx, ty;
int getnum(int x, int y)
{
    int s = 0;
    while(x) {
        s += x % 10;
        x /= 10;
    }
    while(y) {
        s += y % 10;
        y /= 10;
    }
    return s;
}
void dfs(int x, int y)
{
    int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}};
    //枚举4个方向
    for(int i = 0; i < 4; ++i) {
        //下一点坐标
        tx = x + next[i][0];
        ty = y + next[i][1];
        //超出范围
        if(tx < 0 || ty < 0 || tx >= rows || ty >= cols)
            continue;
        //没访问过且小于k
        if(book[tx][ty] == 0 && getnum(tx, ty) <= k) {
            book[tx][ty] = 1; //标记
            dfs(tx, ty); //递归
            book[tx][ty] = 0; //取消标记
        }
    }
    //切记, ans += 1的if判断放外面
    if(vis[x][y] == 0) {
        ans += 1;
        vis[x][y] = 1;
    }
}
int main()
{
    cin>>k>>rows>>cols;
    book[0][0] = 1;
    dfs(0, 0);
    if(rows == 0 || cols == 0)
        cout<<0;
    else
        cout<<ans;
    return 0;
}

-- -- --梳理-- -- --

bfs核心是扩展，dfs核心是递归

相同点

1，方向数组next[4][2]        2,getnum()按题意写（当然有时不需要getnum）

区别

bfs构造完getnum()后，直接进入主函数，通过队列和开头的while(head < tail)得到答案

dfs构造完getnum()后，还要构造dfs()，这才进入主函数，然后调用函数得到答案 

bfs的主体是在主函数里通过队列实现的(也可放函数外)，dfs主体在主函数外通过递归实现 

其实很多迷宫题，都需要getnum()这个函数，当然实现会有点区别

👊（三）188. 武士风度的牛

188. 武士风度的牛 - AcWing题库

标签：搜索，BFS，简单

 

BFS模板，因为不熟悉，我写了50分钟才写出来，然后样例没对。。

找了20分钟，没找到哪里错了，后来别人说，方向数组错了

一开始写成

int next[8][2] = {{1,0},{-1,0},{2,0},{-2,0},
                  {0,1},{0,-1},{0,2},{0,-2}};
...
...
int dd = abs(next[i][0]) - abs(next[i][1]);
            //超出范围或不符合马走势
            if(tx < 0 || ty < 0 || tx >= r || ty >= c || dd == 0)
                continue;

但是dd == 0，并不能保证按马的走，会出现很多(2, 0)，(-2, 0)，(0, 2)，(0, 1)这种玩意

明明之前用过类似的，比如

int next[4][2] = {{-1, 0}, //上
                  {1, 0},  //下
                  {0, -1}, //左
                  {0, 1}}; //右

但这个是迷宫中，每次走一步，结果这次只是换了点东西就错了

思维定势太严重，，，还得多接触下不同的题，培养思考习惯，而不是套模板习惯

方向数组改成这个后

int next[8][2] = {{1,2},{1,-2},{-1,2},{-1,-2},
                  {2,1},{2,-1},{-2,1},{-2,-1}};

我又编了一组测试

6 5
.....
K....
.....
..*..
.....
.*.H.
3

然后提交，AC了

AC  代码

#include<iostream>
#include<cmath> //abs()
using namespace std;
char a[151][151];
int startx, starty, p, q, tx, ty, flag = 0; //p,q 终点坐标
struct node
{
    int x, y, s; //横坐标,纵坐标,步数
};
int main()
{
    //方向数组
    struct node que[22510];
    int next[8][2] = {{1,2},{1,-2},{-1,2},{-1,-2},
                  {2,1},{2,-1},{-2,1},{-2,-1}};
    int c, r; //c列r行
    cin>>c>>r;
    //读入地图
    //记得是从0开始, 后续都受这个影响
    for(int i = 0; i < r; ++i)
        for(int j = 0; j < c; ++j) {
            cin>>a[i][j];
            if(a[i][j] == 'K')
                startx = i, starty = j; //起点
            if(a[i][j] == 'H')
                p = i, q = j; //终点
        }
    //队列初始化
    int head = 0, tail = 0;
    que[tail].x = startx;
    que[tail].y = starty;
    que[tail].s = 0;
    tail++;
    a[startx][starty] = '*'; //标记走过
    //当队列不为空
    while(head < tail) {
        //枚举四个方向
        for(int i = 0; i < 8; ++i) {
            tx = que[head].x + next[i][0];
            ty = que[head].y + next[i][1];
            int dd = abs(next[i][0]) - abs(next[i][1]);
            //超出范围或不符合马走势
            if(tx < 0 || ty < 0 || tx >= r || ty >= c || dd == 0)
                continue;
            //不为障碍且没走过
            if(a[tx][ty] == '.') {
                //bfs每个点只入队一次
                a[tx][ty] = '*'; //标记走过
                que[tail].x = tx;
                que[tail].y = ty;
                que[tail].s = que[head].s + 1;
                tail++;
            }
            if(tx == p && ty == q) {
                flag = 1;
                break;
            }
        }
        if(flag) break;
        head++; //继续后续队列扩展
    }
    cout<<que[tail - 1].s; //tail指向队尾下一位, 要-1
    return 0;
}

👊（四）P1451 求细胞数量

P1451 求细胞数量 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

标签：搜索，BFS，DFS，普及-

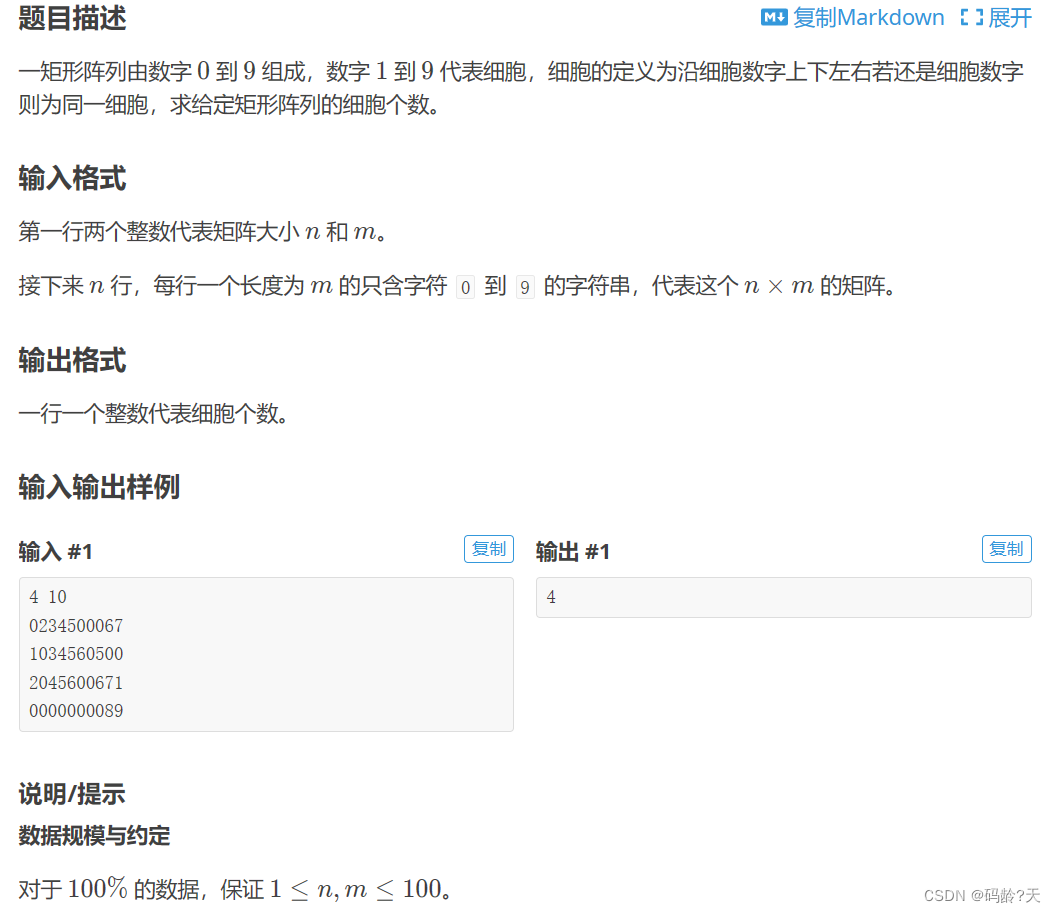
一开始看到分成几块，第一时间以为可以用并查集，想了大半小时没结果，因为一个元素分横纵坐标两个变量，可以考虑用结构体，但比BFS难实现多了

所以没有最好的算法，只有最合适的算法

🌳暴力BFS

基础思路：写个bfs函数，访问过的点标记好

主函数中两层for循环遍历每个点直到所有非0点都遍历过

最后输出细胞数

这里不用book数组，我们直接在存储地图的二维数组a上直接操作，访问过的点赋值为0即可

还要注意下输入问题，可以按我的，转整型再放进二维数组

也可以直接按char[][]输入，直接对字符判断

哪个熟练用哪个

额外的测试

5 7
1024540
0314350
1230123
1213010
1230230
2

AC  代码

#include<iostream>
using namespace std; //string s;
int a[110][110], ans = 0, n, m, tx, ty;
struct node
{
    int x, y; //横坐标, 纵坐标, 编号
};
struct node que[10010]; //100*100
void bfs(int x, int y)
{
    int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组
    //初始化队列
    int head = 0, tail = 0;
    que[tail].x = x;
    que[tail].y = y;
    tail++;
    a[x][y] = 0; //标记
    //队列不为空
    while(head < tail) {
        //枚举4个方向
        for(int i = 0; i < 4; ++i) {
            tx = que[head].x + next[i][0];
            ty = que[head].y + next[i][1];
            //超出范围或不为细胞
            if(tx < 0 || ty < 0 || tx >= n || ty > m || a[tx][ty] == 0)
                continue;
            a[tx][ty] = 0; //标记
            que[tail].x = tx;
            que[tail].y = ty;
            tail++;
        }
        head++; //继续后续点的扩展
    }
}
int main()
{
    cin>>n>>m;
    string s[n];
    //按字符串读入
    for(int i = 0; i < n; ++i)
        cin>>s[i];
    //2维数组建表
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < m; ++j) {
            a[i][j] = s[i][j] - '0'; //字符转10进制整数
        }
    //对所有点BFS
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < m; ++j) {
            if(a[i][j] != 0) {
                bfs(i, j);
                ans += 1;
            }
        }
    cout<<ans;
    return 0;
}

🌳暴力DFS

由于代码第15行，我不确定是否要按模板常规的取消标记（标记，递归，取消标记的套路）

所以，第一次保留了取消标记，输出错误

第二次，去掉了取消标记，输出正确，但是不放心，就又试了一次

额外的测试

4 5
11110
11101
11001
01010
3

居然对了，忘了dfs遇到死胡同，会自动递归回上一步，直到有通路的全部点访问完

AC  代码

#include<iostream>
using namespace std; //string s;
int a[110][110], ans = 0, n, m, tx, ty;
void dfs(int x, int y)
{
    a[x][y] = 0; //标记
    int next[4][2] = {{1,0},{-1,0},{0,1},{0,-1}}; //方向数组
    for(int i = 0; i < 4; ++i) {
        tx = x + next[i][0];
        ty = y + next[i][1];
        if(tx < 0 || ty < 0 || tx >= n || ty >= m || a[tx][ty] == 0)
            continue;
        a[tx][ty] = 0; //标记
        dfs(tx, ty); //递归
    }
}
int main()
{
    cin>>n>>m;
    string s[n];
    //按字符串读入
    for(int i = 0; i < n; ++i)
        cin>>s[i];
    //2维数组建表
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < m; ++j) {
            a[i][j] = s[i][j] - '0'; //字符转10进制整数
        }
    //对所有点BFS
    for(int i = 0; i < n; ++i)
        for(int j = 0; j < m; ++j) {
            if(a[i][j] != 0) {
                dfs(i, j);
                ans += 1;
            }
        }
    cout<<ans;
    return 0;
}

才39行，比bfs少了20行，虽然很多人说dfs难，但好实现

👊（五）1810: [NewOJ Week 4] 超级骑士

P1810 - [NewOJ Week 4] 超级骑士 - New Online Judge (ecustacm.cn)

👂 今晚约会吧（踩着落日余晖） - SORROW - 单曲 - 网易云音乐

标签：进阶题，深搜，广搜

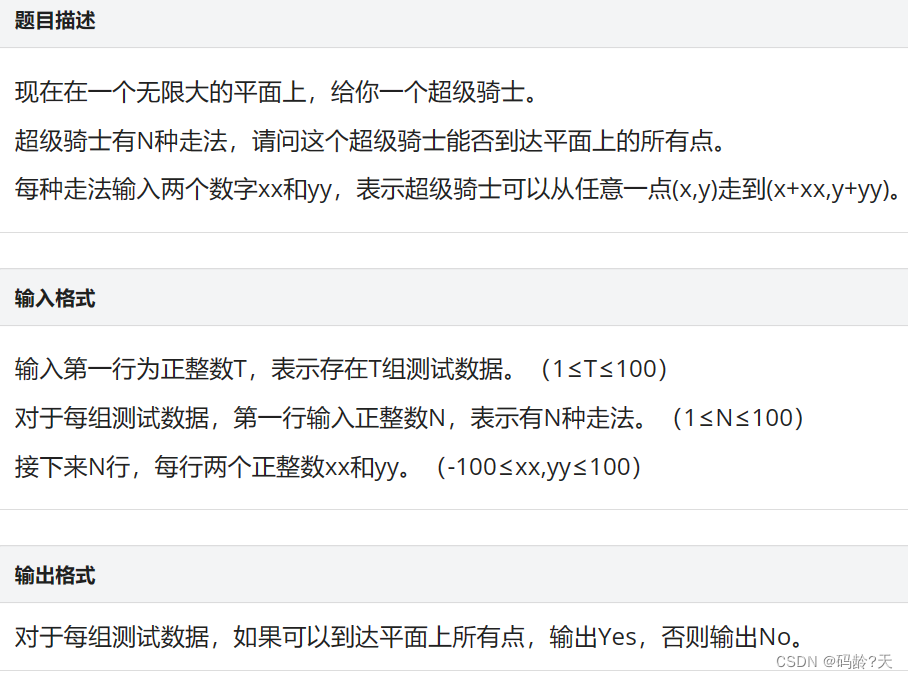
 DFS，BFS都可以，都尝试下

思路

一开始也一头雾水，看了大佬的文字解释，自己再开干

1，如何判断一个骑士可以走遍整个空间？

只要这个骑士能从(x, y)走到(x + 1, y), (x - 1, y), (x, y - 1), (x, y + 1)

则骑士可以走遍平面

2，由于每步坐标不超过100，可以从(100, 100)出发，暴力走(0 ~ 200, 0 ~ 200)的二维平面，最后检查(100, 100)四周是否被标记(走过)

思路来源NewOJ Week 4题解_[newoj week 4] 减一_傅志凌的博客-CSDN博客

里的E题

🌳广搜  AC

第一次提交

运行错误，一般是数组超限

struct node que[40010]; 
--> struct node que[41000];

不够严谨哈，算数也算错，一开始是想到201*201的，但是201 * 201 != 40001， 

200*201 = 200*200+1*200 = 40200，而201*201还得加上201，== 40401

你个菜鸡

修改后提交，AC 90%，时间超限

AC  90%

#include<iostream>
#include<cstring> //memset()
using namespace std;
int vis[205][205]; //标记
int dx[110], dy[110]; //direction方向
int tx, ty; //临时变量
struct node
{
    int x, y; //横纵坐标
};
int main()
{
    struct node que[50010];
    int t;
    cin>>t;
    while(t--) {
        //归0
        memset(que, 0, sizeof(que)); //清空结构体数组
        memset(vis, 0, sizeof(vis)); //清空标记过的点
        int n;
        cin>>n;
        //读入方向
        for(int i = 0; i < n; ++i)
            cin>>dx[i]>>dy[i];
        //初始化队列
        int head = 0, tail = 0;
        que[tail].x = 100;
        que[tail].y = 100;
        tail++;
        vis[100][100] = 1; //标记
        //队列不为空
        while(head < tail) {
            //枚举n个方向
            for(int i = 0; i < n; ++i) {
                tx = que[head].x + dx[i];
                ty = que[head].y + dy[i]; //新的坐标
                //超出边界
                if(tx < 0 || ty < 0 || tx > 200 || ty > 200)
                    continue;
                //未访问过
                if(vis[tx][ty] == 0) {
                    vis[tx][ty] = 1;
                    que[tail].x = tx;
                    que[tail].y = ty;
                    tail++;
                }
            }
            head++; //继续后续队列的扩展
        }
        if(vis[99][100] && vis[101][100]
           && vis[100][99] && vis[100][101])
           cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

应该dfs在这题复杂度稍微低了点的原因，bfs得开scanf()才AC

所有cin改scanf()好了

AC  100%

#include<iostream>
#include<cstring> //memset()
#include<cstdio> //scanf()
using namespace std;
int vis[205][205]; //标记
int dx[110], dy[110]; //direction方向
int tx, ty; //临时变量
struct node
{
    int x, y; //横纵坐标
};
int main()
{
    struct node que[41000];
    int t;
    scanf("%d", &t);
    while(t--) {
        //归0
        memset(que, 0, sizeof(que)); //清空结构体数组
        memset(vis, 0, sizeof(vis)); //清空标记过的点
        int n;
        scanf("%d", &n);
        //读入方向
        for(int i = 0; i < n; ++i)
            scanf("%d%d", &dx[i], &dy[i]);
        //初始化队列
        int head = 0, tail = 0;
        que[tail].x = 100;
        que[tail].y = 100;
        tail++;
        vis[100][100] = 1; //标记
        //队列不为空
        while(head < tail) {
            //枚举n个方向
            for(int i = 0; i < n; ++i) {
                tx = que[head].x + dx[i];
                ty = que[head].y + dy[i]; //新的坐标
                //超出边界
                if(tx < 0 || ty < 0 || tx > 200 || ty > 200)
                    continue;
                //未访问过
                if(vis[tx][ty] == 0) {
                    vis[tx][ty] = 1;
                    que[tail].x = tx;
                    que[tail].y = ty;
                    tail++;
                }
            }
            head++; //继续后续队列的扩展
        }
        if(vis[99][100] && vis[101][100]
           && vis[100][99] && vis[100][101])
           cout<<"Yes"<<endl;
        else cout<<"No"<<endl;
    }
    return 0;
}

 emmm...有大佬跟我说，不开scanf()，bfs也能AC

说没必要用数组模拟队列，直接用stl的#include<queue>就好，更快一点

🌳深搜  AC

#include<iostream>
#include<cstring> //memset()
int vis[210][210], dx[110], dy[110];
int t, n, tx, ty;
void dfs(int x, int y)
{
    for(int i = 0; i < n; ++i) {
        tx = x + dx[i];
        ty = y + dy[i];
        if(tx < 0 || ty < 0 || tx > 200 || ty > 200)
            continue;
        if(vis[tx][ty] == 0) {
            vis[tx][ty] = 1;
            dfs(tx, ty);
            //不用取消标记了
        }
    }
}
using namespace std;
int main()
{
    cin>>t;
    while(t--) {
        memset(vis, 0, sizeof(vis));
        cin>>n;
        for(int i = 0; i < n; ++i)
            cin>>dx[i]>>dy[i];
        vis[100][100] = 1;
        dfs(100, 100);
        if(vis[99][100] && vis[101][100] && vis[100][99] && vis[100][101])
            cout<<"Yes"<<endl;
        else
            cout<<"No"<<endl;
    }
    return 0;
}

难以置信，居然只有37行，而BFS写了58行，大概少20行

由于第一遍写了2次BFS，DFS只写了13分钟

🌼十三，

 👂 理想世界 - 马良 - 单曲 - 网易云音乐

🌼十四，

👂  不露声色 - Jam - 单曲 - 网易云音乐

🌼十五，Dijkstra

👂 这个世界不会好 - 子默 - 单曲 - 网易云音乐

dijkstra科普博客👇

→ (13条消息) 最短路之Dijkstra（15张图解）_迪杰斯特拉算法求最短路径图解_码龄?天的博客-CSDN博客

→ 

→ 

→ 

先来默写一下dijkstra模板（结合输入输出）

第一行输入n个顶点，m条边

后面m行输入 t1 号顶点到 t2 号顶点的距离 t3

最后一行输出 1 号顶点到 1~n 号顶点的最短路径

代码

#include<cstdio>
int main()
{
    int e[10][10], dis[10], book[10], i, j, n, m;
    int t1, t2, t3, u, v, Min;
    int inf = 1e8; //infinity(n.)无穷

    //读入n个顶点, m条边
    scanf("%d%d", &n, &m);

    //初始化
    for(i = 1; i <= n; ++i)
        for(j = 1; j <= n; ++j) {
            if(i == j) e[i][j] = 0;
            else e[i][j] = inf;
        }

    //读入边
    for(i = 1; i <= m; ++i) {
        scanf("%d%d%d", &t1, &t2, &t3);
        e[t1][t2] = t3;
    }

    //初始化dis数组, 表示源点1号到其他点初始路程
    for(i = 1; i <= n; ++i)
        dis[i] = e[1][i];

    //初始化book数组
    for(i = 1; i <= n; ++i)
        book[i] = 0;

    //Dijkstra算法核心
    //源点不用确定, 所以是n - 1次遍历
    for(i = 1; i <= n - 1; ++i) {
        Min = inf;
        for(j = 2; j <= n; ++j) { //从顶点2开始
            //找确定值（未确定中找最小值）
            if(book[j] == 0 && dis[j] < Min) {
                Min = dis[j];
                u = j;
            }
        }
        book[u] = 1; //顶点u已确定
        //从刚被确定的顶点出边
        for(v = 2; v <= n; ++v) //从顶点2开始
            if(e[u][v] < inf && dis[u] + e[u][v] < dis[v])
            //两点连通且可更新
                dis[v] = dis[u] +e[u][v];
    }
    for(int i = 1; i <= n; ++i)
        printf("%d ", dis[i]);

    return 0;
}

输入输出

6 9
1 2 1
1 3 12
2 3 9
2 4 3
3 5 5
4 3 4
4 5 13
4 6 15
5 6 4
0 1 8 4 13 17

🌼十六，

👂 世间美好与你环环相扣 - 柏松 - 单曲 - 网易云音乐

🌼十七，

👂 我才不看你脸色！ - 蛙腩/AEolus阿一 - 单曲 - 网易云音乐

🌼十八，

👂 声声慢 - 崔开潮 - 单曲 - 网易云音乐

🌼十九，

👂 渡渡年 - 要不要买菜 - 单曲 - 网易云音乐

🌼二十，

👂 風になる（幻化成风） - つじあやの - 单曲 - 网易云音乐

🍋总结 

大一参加蓝桥杯注定无法取得好成绩，因为数据结构是大二上才学，先不谈数据结构，单就算法来说，大一能掌握一半的基础算法都不错了，只是一半的基础算法，最多也就C++A组省二

1，对拍，找bug很棒的方法

2，s.find(), s.substr() 

#include<cstring> //s.substr(), s.find()

string s1 = s.substr(j, i); //下标j开始, 截取i个字符
if(s.find(s1, j + 1) == string::npos)
//没有找到子串, 返回string::npos

if(s.find(s1, j + 1) != string::npos)
//找到子串

3，map的迭代器

#include<iostream>
#include<map>
using namespace std;
map<int, int>m;
for(map<int, int>::iterator it = m.begin(); it != m.end(); ++it) //迭代器
    printf("%d ", it->second);

4，蓝桥杯技巧

不论是比赛还是平时，OI赛制都要懂得自己设计样例来测试代码，不要只是过了样例就提交

也许有些简单的错误是样例测试不出来的

样例过了后，再想2~5组数据，都过了再提交，没过就好好检查下为什么信心满满的代码不行，总能揪出错误

5，O2优化

洛谷或者AcW里少数的题会卡O2，起到常数优化的效果

代码第一行加上：#pragma GCC optimize(2)

#pragma GCC optimize(2)

蓝桥杯是可以用的

6，数组超限

是个大坑，比如201 * 201的二维平面，你得开到40401以上，而不是40001以上，因为 201 * 201 = 40401，心算不好就拿🖊算，要么就多开个几千