题目来源
1049. 最后一块石头的重量 II

思路

最后一块石头的重量，两个近似的石头值相近，那么最后一块石头的重量最小
举例:stones = [2,7,4,1,8,1]
总和sum=23，我们取目标值target=sum/2=11，我们需要找到<=11最大的数值ans（可能里面没有刚好加起来等于11的，但是有<11最大的），找到的数值是ans.
sum-ans=另一半的值（另一半的值一定大于ans，因为target里面用的/向下取整）
(sum-ans)-ans=最后一块石头的重量

回溯法

class Solution {
    int ans = 0;
    public int lastStoneWeightII(int[] stones) {
        int stonesSum = 0;
        //求所有石头的总和
        for(int stone:stones){
            stonesSum += stone;
        }
        int target = stonesSum / 2;
        backTracking(stones,0,0,target);
        ans = stonesSum - ans -ans;
        return ans;
    }
    
    private void backTracking(int[] stones,int sum,int startIndex,int target){
        //如果sum小于target，就一直累积ans的最大值，记得不要return
        if(sum < target){
            ans=Math.max(ans,sum);
        }
        //sum==target直接返回结果
        if(sum == target){
            ans = sum;
            return;
        }
        //剪枝，如果sum>target接下来的就不要计算了
        if(sum > target){
            return;
        }

        for(int i = startIndex;i<stones.length;i++){
            sum += stones[i];
            //i+1目的是为了不选取重复元素
            backTracking(stones,sum,i+1,target);
            sum -= stones[i];  //回溯
        }
    }
}

动态规划

理解了0-1背包问题，直接搬照着公式就可以写出
https://donglin.blog.csdn.net/article/details/129412502

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int stone : stones){
            sum += stone;
        }
        int target = sum / 2;
        //为啥是1501，题目给的1 <= stones.length <= 30 1 <= stones[i] <= 100最大总和3000
        int[][] dp = new int[stones.length][1501];
        for(int j = stones[0];j<=target;j++){
            dp[0][j] = stones[0];
        }
        for(int i = 1;i<stones.length;i++){
            for(int j = 1;j<=target;j++){
                if(j < stones[i]){
                    dp[i][j] = dp[i-1][j];
                }else{
                    dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]);
                }
            }
        }
        return sum - dp[stones.length-1][target]*2;
    }

}

动态规划(压缩)

• 1.确定dp数组以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。
相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”

• 2.确定递推公式

如果不清楚0-1背包问题的一维数组，可以看这篇
https://donglin.blog.csdn.net/article/details/129437136
01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

• 3.dp数组如何初始化

因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 100，所以最大重量就是30 * 100 。
而我们要求的target其实只是最大重量的一半，所以dp数组开到1500大小就可以了。
当然也可以把石头遍历一遍，计算出石头总重量 然后除2，得到dp数组的大小。
我这里就直接用1500了。

        int[] dp = new int[1501];

• 4.确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！

        for(int i = 0;i<stones.length;i++){
            for(int j = target;j>=stones[i];j--){
                dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }

• 5.举例推导dp数组

举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：

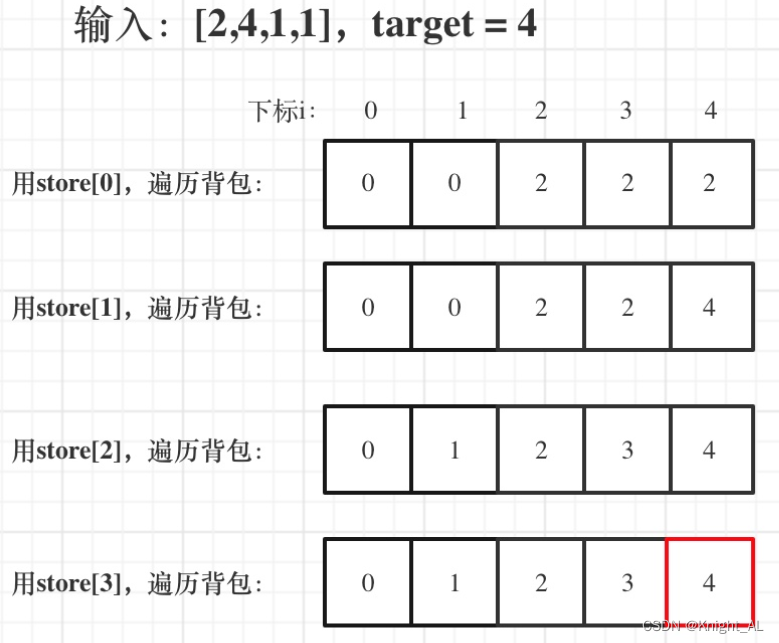
最后dp[target]里是容量为target的背包所能背的最大重量。
那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。
在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。

那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int stone : stones){
            sum += stone;
        }
        int target = sum / 2;
        //为啥是1501，题目给的1 <= stones.length <= 30 1 <= stones[i] <= 100最大总和3000
        int[] dp = new int[1501];
        for(int i = 0;i<stones.length;i++){
            for(int j = target;j>=stones[i];j--){
                dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        return sum - dp[target] -dp[target];
    }

}