[acwing周赛复盘] 第 94 场周赛20230311
- 一、本周周赛总结
- 二、 4870. 装物品
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、4871. 最早时刻
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、4872. 最短路之和
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
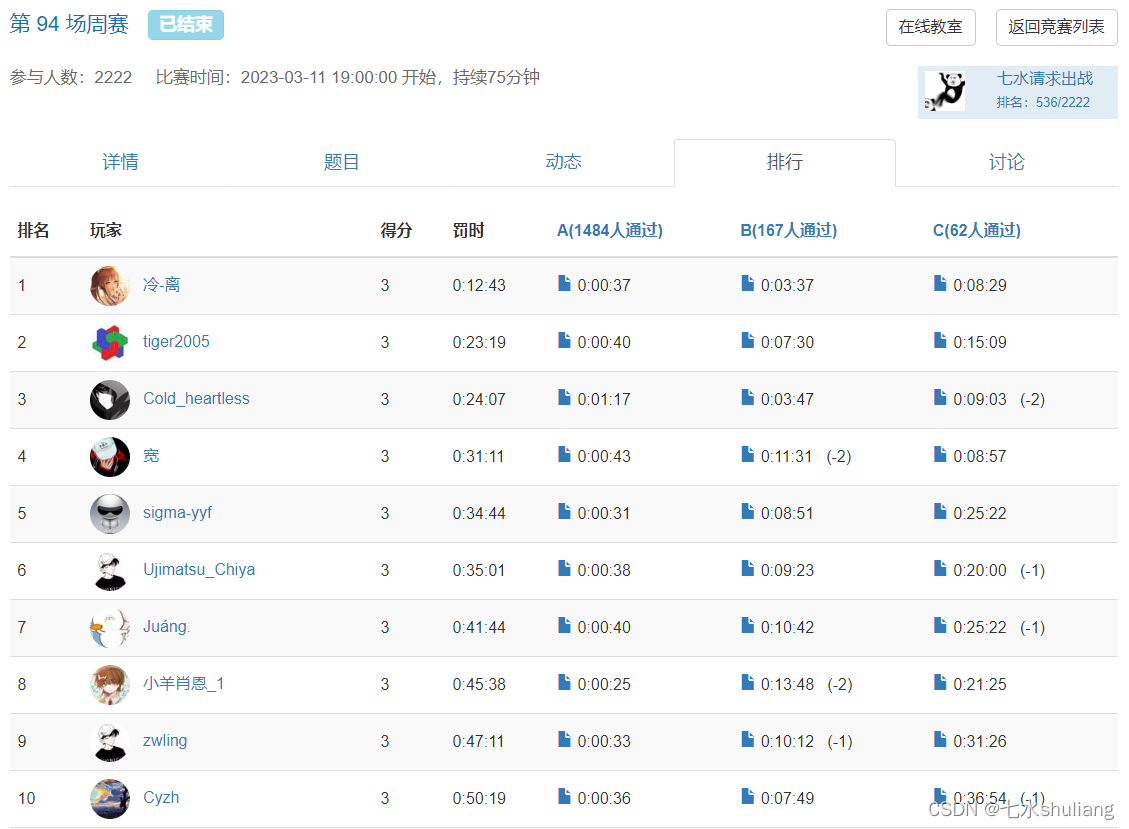
- 又是笨比的一周,只做出1题。
- T1 数学
- T2 单源最短路dijikstra
- T3 多源最短路floyd
二、 4870. 装物品
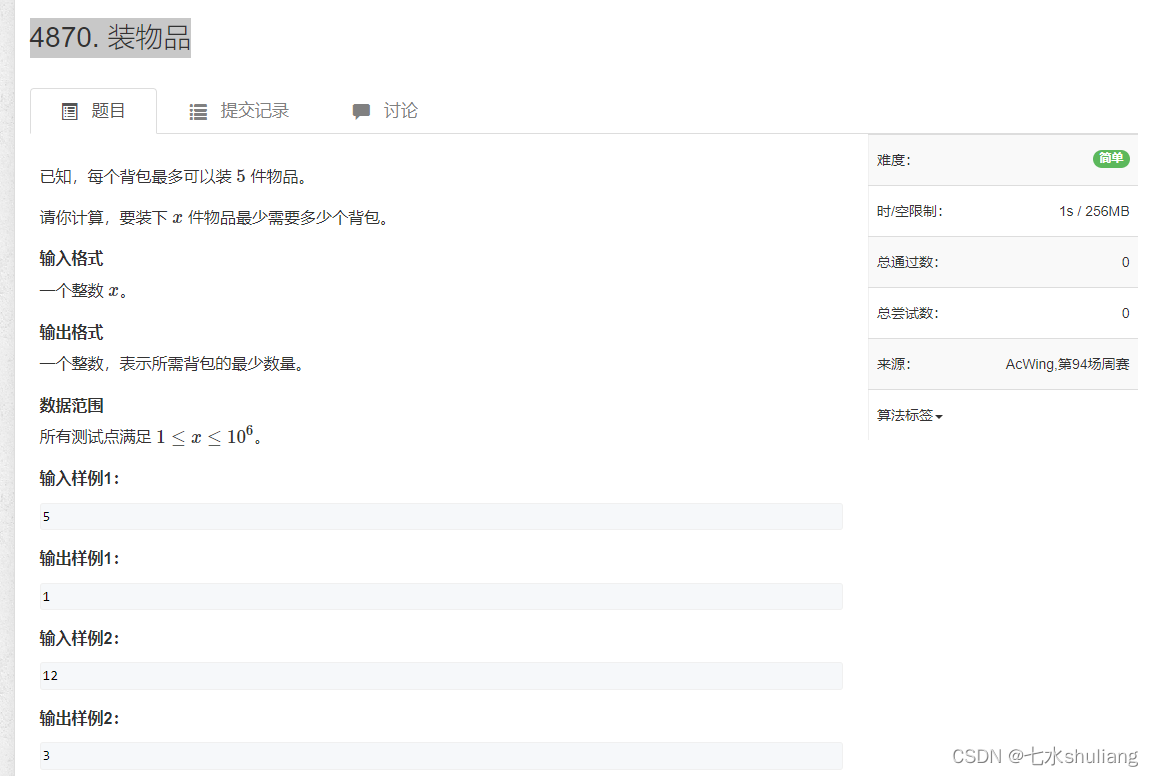
链接: 4870. 装物品
1. 题目描述
2. 思路分析
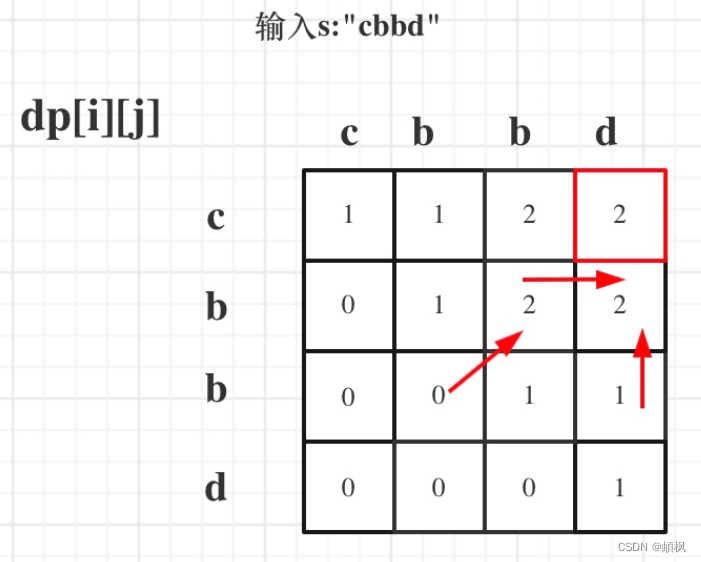
- 所有人都应该知道上取整公式:
- ceil(a/b) = (a+b-1)//b
3. 代码实现
import sys
import bisect
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# ms
def solve():
x, = RI()
print((x+5-1)//5)
if __name__ == '__main__':
solve()
三、4871. 最早时刻
链接: 4871. 最早时刻
1. 题目描述
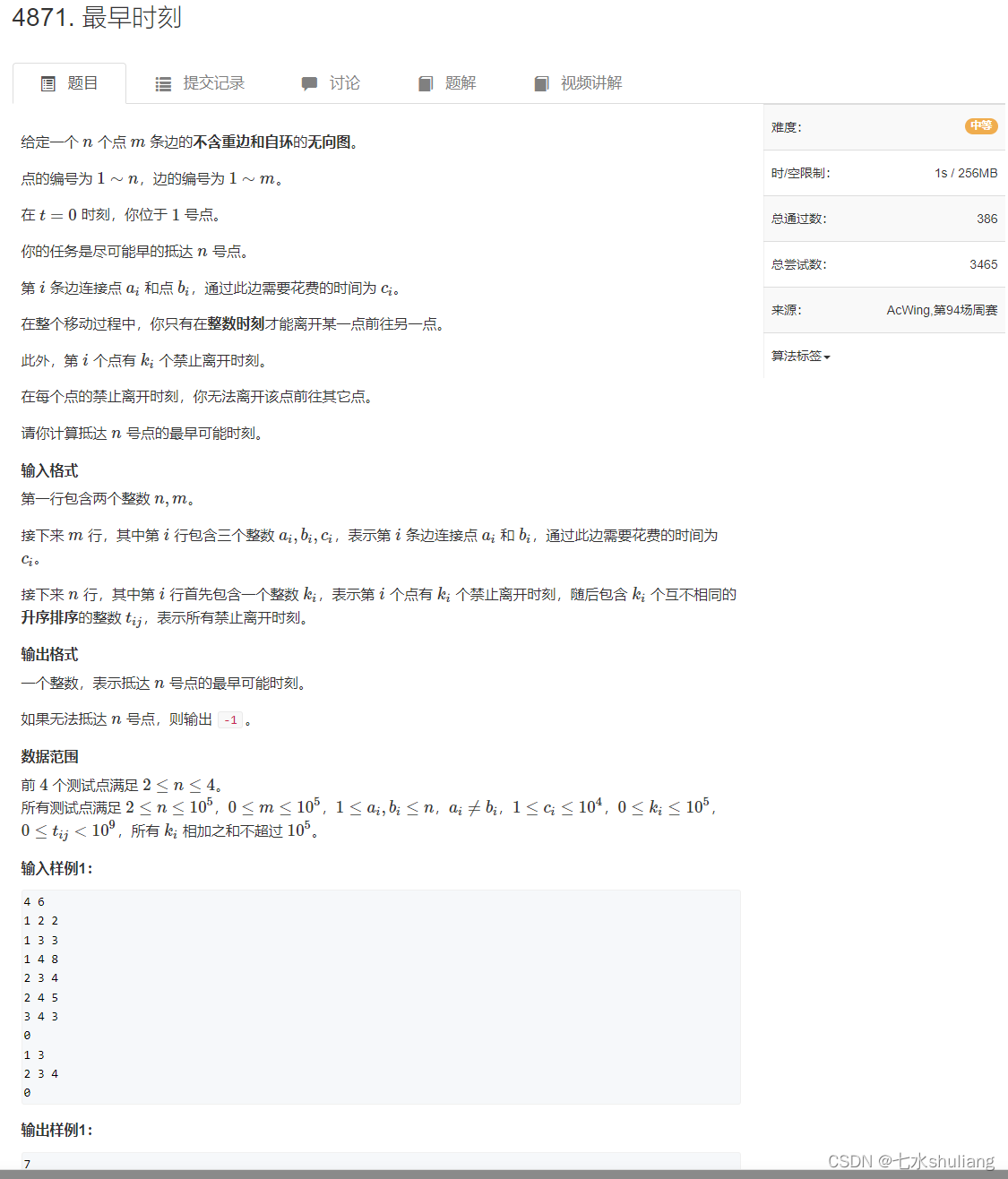
2. 思路分析
脑子木了,一直在想二分怎么不对;而且还写错变量名。。
- 是个比较显然的dijkstra,但是多了个限制条件,有的时间点不能出发。
- 那么可以提前预处理出每个节点位置,所有不能走的时间点,它最早能走的时间。
- 这里一个倒序dp即可。最后一个时间点能走的时间显然是b[-1]+1.
- 向前遍历,如果b[i]后边的数不是b[i]+1,则它在b[i]+1能走;否则就是更后边最近的那个能走的时间点。
- 那么转移的时候出发时间转换一下即可。
- 注意dijkstra每个节点只会访问一次,要记得写
if d>vis[d]:continue因此其实b可以不预处理,直接暴力。
3. 代码实现
# Problem: 最早时刻
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4874/
# Memory Limit: 256 MB
# Time Limit: 1000 ms
import sys
from heapq import *
from math import inf
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# 4330 ms
def solve():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(m):
u, v, w = RI()
u -= 1
v -= 1
g[u].append((v, w))
g[v].append((u, w))
gogo = []
for _ in range(n):
_, *b = RI()
can = {}
if b:
go = b[-1] + 1
can[b[-1]] = go
for i in range(len(b) - 2, -1, -1):
if b[i] + 1 != b[i + 1]:
go = b[i] + 1
can[b[i]] = go
gogo.append(can)
vis = [inf] * n
vis[0] = 0
h = [(0, 0)]
while h:
d, u = heappop(h)
if u == n - 1:
return print(d)
if d > vis[u]:continue # 巨量优化记得写
ban = gogo[u]
go = ban.get(d, d)
for v, w in g[u]:
nd = go + w
if vis[v] > nd:
vis[v] = nd
heappush(h, (nd, v))
# if n - 1 in vis:
# return print(vis[n - 1])
print(-1)
if __name__ == '__main__':
solve()
四、4872. 最短路之和
链接: 4872. 最短路之和
1. 题目描述
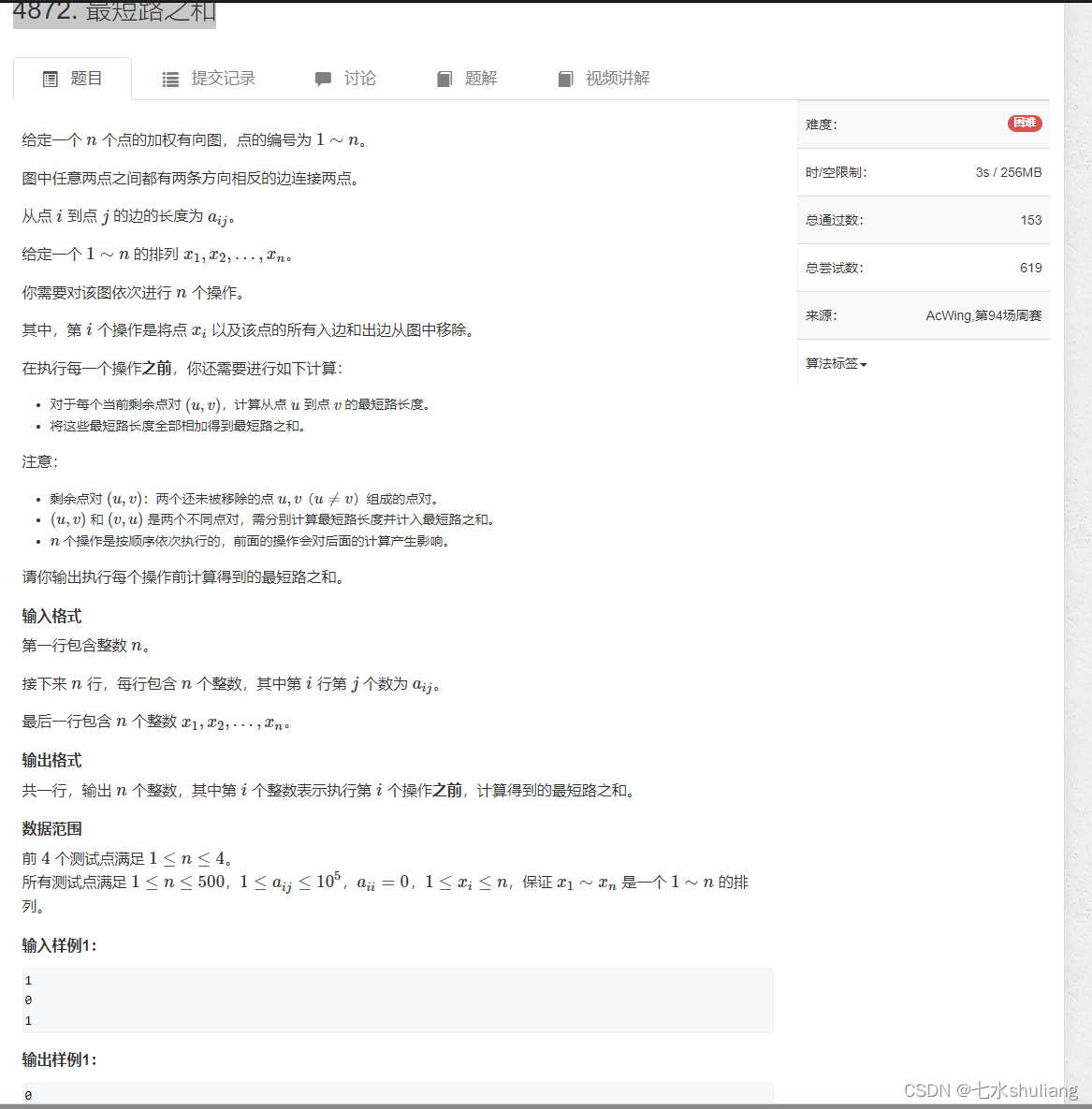
2. 思路分析
傻了,想到了floyd,但没做出来。赛后写了2个代码。都应该掌握。
- 显然这题是个倒序做的题,把x从后一直加到集合里计算即可。
- 方法1,直观且短。把x作为k(去松弛别人的节点),去遍历松弛。
- 由于在floyd里,k是最外层的节点,因此这么做完后,k的影响已经结束了,则可以更新当前答案。
- 实现时,松弛的话是u,v都是全部节点;计算答案只计算已添加的节点。
- 方法2,助于理解floyd。
- 依然倒序把x作为k,但是分别计算三种最短路:k到所有已访问的u、所有u到k、所有已访问的u到v。
- 这里注意计算顺序,由于u->v是已经计算完的最短路,所以必须用它们先去更新k相关的最短路,再返回来计算新的u->v。
3. 代码实现
# Problem: 最短路之和/*-/*-/*-/*-
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4875/
# Memory Limit: 256 MB
# Time Limit: 3000 ms
import sys
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
PROBLEM = """
"""
# 6995 ms
def solve():
n, = RI()
d = []
for _ in range(n):
d.append(RILST())
xs = RILST()
ans = []
ps = []
for x in xs[::-1]:
k = x - 1
# 注意 上两个循环可以合并(顺序随意),但这个循环必须在最后,否则会wa
# 前提是所有其它点到k的最短路(即所有uk/kv)求出来,才可以用k来松弛uv的边。
for u in range(n):
for v in range(n):
d[u][v] = min(d[u][v], d[u][k] + d[k][v])
ps.append(k)
a = 0
for u in ps:
for v in ps:
a += d[u][v]
ans.append(a)
print(*(ans[::-1]))
# 10039 ms
def solve1():
n, = RI()
d = []
for _ in range(n):
d.append(RILST())
xs = RILST()
ans = []
ps = []
for x in xs[::-1]:
k = x - 1
a = 0
# 尝试用所有v松弛uk,这里uv已经是最短路,所以可以松弛
for u in ps:
for v in ps:
d[u][k] = min(d[u][k], d[u][v] + d[v][k])
a += d[u][k]
# 尝试用所有v松弛ku,这里uv已经是最短路,所以可以松弛
for u in ps:
for v in ps:
d[k][u] = min(d[k][u], d[k][v] + d[v][u])
a += d[k][u]
# 注意 上两个循环可以合并(顺序随意),但这个循环必须在最后,否则会wa
# 前提是所有其它点到k的最短路(即所有uk/kv)求出来,才可以用k来松弛uv的边。
for u in ps:
for v in ps:
d[u][v] = min(d[u][v], d[u][k] + d[k][v])
a += d[u][v]
ps.append(k)
ans.append(a)
print(*(ans[::-1]))
if __name__ == '__main__':
solve()
六、参考链接
- 无