一【题目类别】

深度优先搜索

二【题目难度】

简单

三【题目编号】

783.二叉搜索树节点最小距离

四【题目描述】

给你一个二叉搜索树的根节点 root ，返回树中任意两不同节点值之间的最小差值。
差值是一个正数，其数值等于两值之差的绝对值。

五【题目示例】

示例 1：
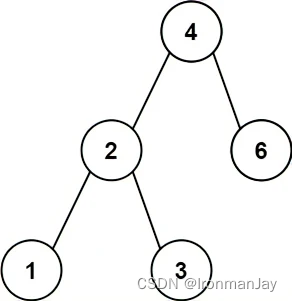
- 输入：root = [4,2,6,1,3]
- 输出：1
示例 2：
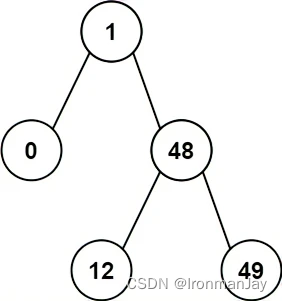
- 输入：root = [1,0,48,null,null,12,49]
- 输出：1

六【解题思路】

此题比较简单，利用二叉搜索树的性质：对二叉搜索树进行中序遍历，会得到升序序列
既然是升序序列，所以最小差值一定在相邻值中出现，所以只需要使用pre记录当前节点root的前驱节点，记录差值进行比较，如果有更小的差值就更新
最后返回结果即可

七【题目提示】

$树中节点的数目范围是 [2, 100]$
$0 <= Node.val <= 10^5$

八【题目注意】

本题与 530：https://leetcode-cn.com/problems/minimum-absolute-difference-in-bst/ 相同

九【时间频度】

时间复杂度： $O (n)$ ，其中 $n$ 为传入二叉树的节点个数
空间复杂度： $O (n)$ ，其中 $n$ 为传入二叉树的节点个数

十【代码实现】

Java语言版

class Solution {

    TreeNode pre = null;
    int min = Integer.MAX_VALUE;

    public int minDiffInBST(TreeNode root) {
        inOrder(root);
        return min;
    }

    public void inOrder(TreeNode root){
        if(root != null){
            inOrder(root.left);
            if(pre != null){
                min = Math.min(min,Math.abs(pre.val - root.val));
            }
            pre = root;
            inOrder(root.right);
        }
    }

}

C语言版

void inOrder(struct TreeNode* root,int* pre,int* min)
{
    if(root != NULL)
    {
        inOrder(root->left,pre,min);
        if(*pre != -1)
        {
            *min = fmin(*min,abs(root->val - (*pre)));
        }
        *pre = root->val;
        inOrder(root->right,pre,min);
    }
}

int minDiffInBST(struct TreeNode* root)
{
    int* pre = -1;
    int min = INT_MAX;
    inOrder(root,&pre,&min);
    return min;
}

Python语言版

class Solution:
    def minDiffInBST(self, root: Optional[TreeNode]) -> int:
        def inOrder(root):
            nonlocal res,pre
            if root != None:
                inOrder(root.left)
                if pre != -1:
                    res = min(res,abs(root.val - pre))
                pre = root.val
                inOrder(root.right)
        pre = -1
        res = float('inf')
        inOrder(root)
        return res

C++语言版

class Solution {
public:
    void inOrder(TreeNode* root,int& pre,int& res)
    {
        if(root != nullptr)
        {
            inOrder(root->left,pre,res);
            if(pre != -1)
            {
                res = min(res,abs(root->val - pre));
            }
            pre = root->val;
            inOrder(root->right,pre,res);
        }
    }

    int minDiffInBST(TreeNode* root) 
    {
        int pre = -1;
        int res = INT_MAX;
        inOrder(root,pre,res);
        return res;
    }
};