前言

BFS是一种朴素的最短路算法，它可以找到无权图或边权都相同的图的最短路，但是对于边权不完全相同甚至可能是负数的图，BFS并不能得到正确的结果，此时我们就需要使用其他的最短路算法来求解。

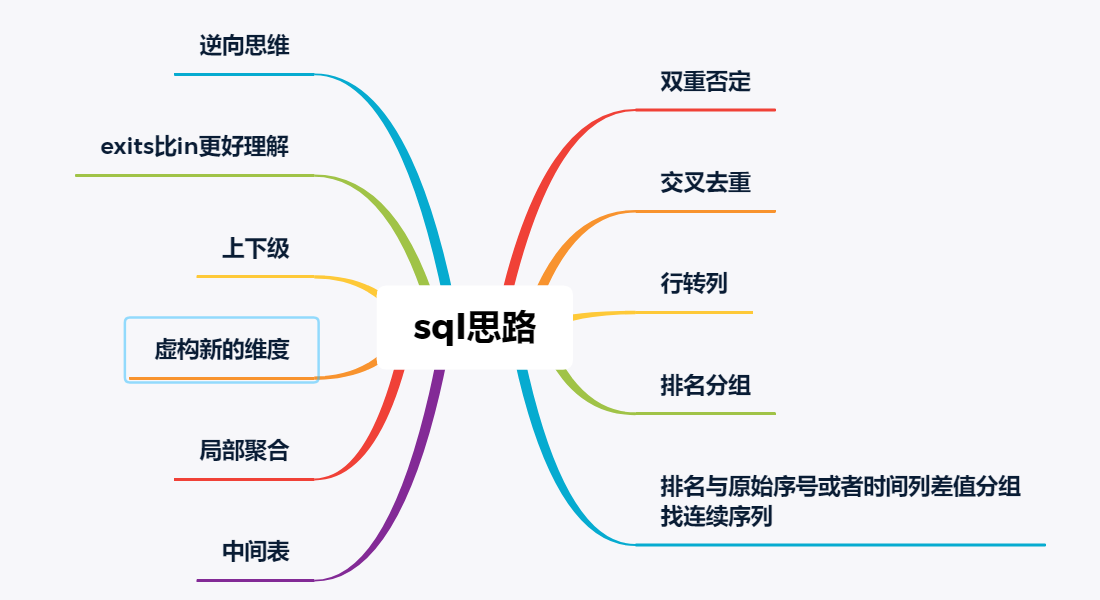
本文仅介绍最基础的几种最短路算法，思维导图如下：

单源最短路指的是给定一个源点，计算该源点到图中所有其他点的最短路径长度，而全源最短路则是计算图中任意两点之间的最短路径长度。

为方便叙述，接下来均假定图中节点的数量为 $n$ ，边的数量为 $m$ ，节点的编号为 $1\sim n$ 。

一、全源最短路

1.1 Floyd

Floyd算法是一种求解图中任意两点之间最短路径的经典算法，它适用于任何图，不管有向无向，边权正负，但是最短路必须存在（不能有个负环）。

该算法的基本思想是动态规划，具体来讲，定义一个三维数组 dp[k][x][y]，表示从起点 $x$ 经过子图 $G^{'}$ 后到达终点 $y$ 的最短路径的长度，其中 $G^{'}$ 由节点 $1,2,\cdots,k$ 构成（ $x$ 和 $y$ 不一定在 $G^{'}$ 中）。

由上述定义可知，dp[n][x][y] 即为 $x$ 到 $y$ 的最短路径长度（因为此时 $G^{'} = G$ ），dp[0][x][y] 为 $x$ 到 $y$ 的边权。

为计算 $d p [k] [x] [y]$ ，我们可以将其分为以下两种情况考虑：

不经过节点 $k$ ：即 $d p [k - 1] [x] [y]$ ；
经过节点 $k$ ：那么从 $x$ 到 $y$ 的最短距离变成了 $x$ 到 $k$ 的最短距离加上 $k$ 到 $y$ 的最短距离，即 $d p [k - 1] [x] [k] + d p [k - 1] [k] [y]$ 。

于是可得递推式：

$\min(dp[k-1][x][y], \;dp[k-1][x][k]+dp[k-1][k][y]),\quad k,x,y\geq 1$

对应求解代码如下：

for (int k = 1; k <= n; k++)
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            dp[k][i][j] = min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]);

我们可以使用滚动数组将其优化成二维的形式：

for (int k = 1; k <= n; k++)
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);

注意到要想求 dp[1][..][..] 必须先求得 dp[0][..][..]，而 dp[0][..][..] 实际上就是图的邻接矩阵，因此我们可以直接在图的邻接矩阵上进行动态规划。计算结束后，dp[a][b] 就代表了 $a$ 到 $b$ 的最短距离。

🔗 AcWing 854. Floyd求最短路

#include <bits/stdc++.h>

using namespace std;

const int N = 210, INF = 0x3f3f3f3f;

int n, m, q;
int d[N][N];

void floyd() {
    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
            if (i == j) d[i][j] = 0;  // 干掉自环
            else d[i][j] = INF;

    while (m--) {
        int x, y, z;
        cin >> x >> y >> z;
        d[x][y] = min(d[x][y], z);  // 本来应当是d[x][y] = z，这里取min是为了处理重边
    }

    floyd();

    while (q--) {
        int a, b;
        cin >> a >> b;
        if (d[a][b] > INF / 2) cout << "impossible\n";
        else cout << d[a][b] << "\n";
    }

    return 0;
}

容易看出，Floyd算法的时间复杂度为 $O(n^3)$ ，空间复杂度为 $O(n^2)$ 。

二、单源最短路

2.1 Dijkstra

Dijkstra算法是一种求解非负权图上单源最短路径的贪心算法。

具体来说，Dijkstra算法维护一个集合 $S$ ，其中包含已经确定最短路径的节点，以及一个集合 $\ S V\backslash S$ ，其中包含未确定最短路径的节点。初始时， $S$ 只包含源节点， $\ S V\backslash S$ 包含其余所有节点。然后，算法不断从 $\ S V\backslash S$ 中选出距离源节点最近的一个节点，将其加入到 $S$ 中，并且更新其邻居节点到源节点的距离。重复执行这个过程，直到目标节点被加入到 $S$ 中，或者 $\ S V\backslash S$ 为空为止。

我们需要维护一个距离数组 $d$ ，不妨设编号为 $1$ 的节点是源点，则 $d$ 初始时应当满足 $d[1]=0,\,d[2..n]=+\infty$ 。

🔗 AcWing 849. Dijkstra求最短路 I

稠密图上，我们可以用邻接矩阵来实现：

#include <bits/stdc++.h>

using namespace std;

const int N = 510, INF = 0x3f3f3f3f;

int n, m;
int g[N][N];  // 稠密图用邻接矩阵
int d[N];  // 存储每个点到源点的距离
bool st[N];  // 用来标记一个节点是否已被加入到S中

int dijkstra() {
    // 初始化距离数组
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;

    // 循环n-1次即可，因为第n次循环毫无意义
    for (int i = 0; i < n - 1; i++) {
        // 找到距离源点最近且不在S中的节点
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || d[j] < d[t]))
                t = j;

        st[t] = true;

        // 用该点去更新其邻居节点的距离
        // 对于节点j，若j属于S，则d[j]并不会被覆盖掉，因为一定有d[j] <= d[t]
        // 若t与j不相连，则d[j]也不会更新，因为g[t][j] == INF
        for (int j = 1; j <= n; j++)
            d[j] = min(d[j], d[t] + g[t][j]);
    }

    return d[n] == INF ? -1 : d[n];
}


int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    memset(g, 0x3f, sizeof(g));

    cin >> n >> m;
    while (m--) {
        int x, y, z;
        cin >> x >> y >> z;
        g[x][y] = min(g[x][y], z);  // 处理重边
    }

    cout << dijkstra() << "\n";

    return 0;
}

稀疏图上，我们可以用邻接表来实现（本题是稠密图，这里仅仅是为了展示邻接表的写法）：

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 1e5 + 10, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[M], ne[M], w[M], idx;
int d[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra() {
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;

    for (int i = 0; i < n - 1; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || d[j] < d[t]))
                t = j;

        st[t] = true;

        for (int j = h[t]; ~j; j = ne[j]) {
            int k = e[j];
            d[k] = min(d[k], d[t] + w[j]);
        }
    }

    return d[n] == INF ? -1 : d[n];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    memset(h, -1, sizeof(h));

    cin >> n >> m;
    while (m--) {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }

    cout << dijkstra() << "\n";

    return 0;
}

容易看出，朴素版的Dijkstra算法的时间复杂度为 $O(n^2)$ 。

2.1.1 堆优化版的Dijkstra

先前我们在寻找 t 时（距离源点最近且不在 $S$ 中的点）采用了暴力的做法，时间复杂度是 $O (n)$ 。如果用小根堆来存储距离和编号，则查询 t 的时间复杂度将降至 $O (1)$ 。

🔗 AcWing 850. Dijkstra求最短路 II

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;

const int N = 2e5, INF = 0x3f3f3f3f;

int n, m;
int h[N], e[N], ne[N], w[N], idx;
int d[N];
bool st[N];

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}

int dijkstra() {
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;

    priority_queue<PII, vector<PII>, greater<>> pq;
    pq.emplace(0, 1);  // 第一个放距离，第二个放节点编号，因为pair总是优先排序第一个元素

    while (!pq.empty()) {
        auto [_, t] = pq.top();  // 结构化绑定，因为不需要第一个元素所以用_来占位
        pq.pop();

        if (st[t]) continue;
        st[t] = true;

        for (int i = h[t]; ~i; i = ne[i]) {
            int j = e[i];
            if (d[j] > d[t] + w[i]) {
                d[j] = d[t] + w[i];
                pq.emplace(d[j], j);
            }
        }
    }

    return d[n] == INF ? -1 : d[n];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    memset(h, -1, sizeof(h));

    cin >> n >> m;
    while (m--) {
        int x, y, z;
        cin >> x >> y >> z;
        add(x, y, z);
    }

    cout << dijkstra() << "\n";

    return 0;
}

优化后的时间复杂度为 $O(m\log n)$ 。

由此可见，在稠密图中， $m\approx n^2$ ，此时应当用朴素版的Dijkstra算法；而在稀疏图中， $m\ll n^2$ ，此时应当用堆优化版的Dijkstra算法。

2.2 Bellman-Ford

Dijkstra不能解决负权边是因为当标记 st[j] = true 后，d[j] 就是最短距离了，之后就不能再被更新了（当有负权边时，贪心算法容易得到局部最优而不是全局最优）。如下图所示：

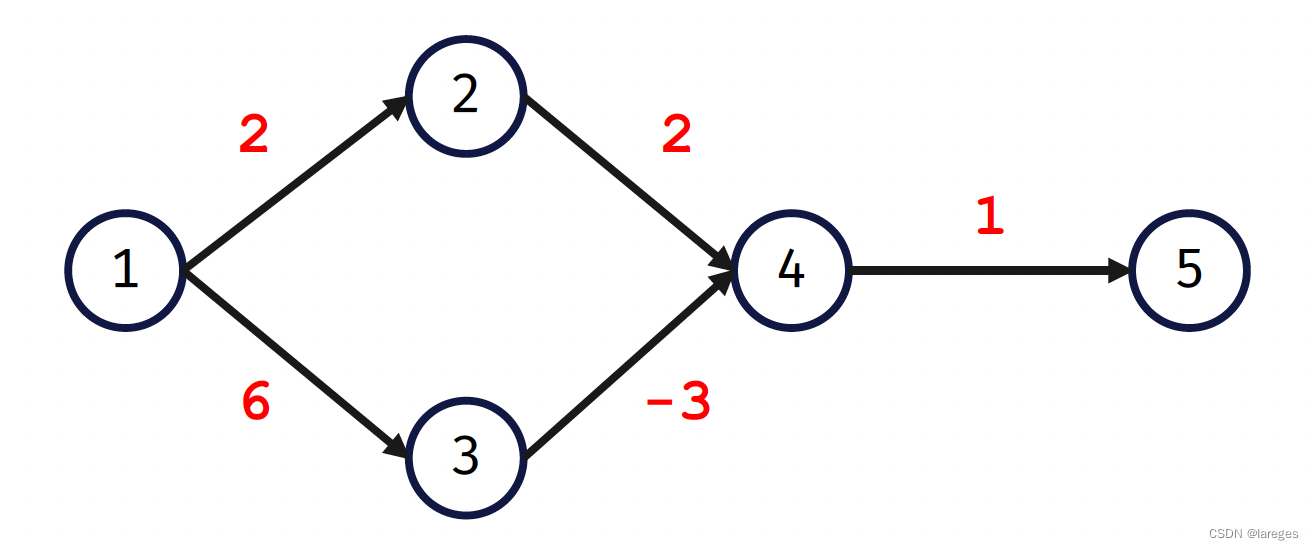
Dijkstra算法会依次标记 1 -> 2 -> 4 -> 5，当标记 5 之后，1 到 5 的最短路就确定了，而实际的最短路却是 1 -> 3 -> 4 -> 5。

Bellman-Ford算法不断尝试对图上每一条边进行松弛，例如，对于边 $a\xrightarrow{w} b$ ，该边的松弛操作为

$\min(d[b],\,d[a] + w)$

其中 $d [x]$ 表示 $1$ 号点（起点）到 $x$ 号点的最短距离。

每进行一轮循环，该算法就会对图上所有边都进行一次松弛操作。因此当循环 $k$ 次后，边数不超过 $k$ 的最短路就可以确定。

🔗 AcWing 853. 有边数限制的最短路

#include <bits/stdc++.h>

using namespace std;

const int N = 510, M = 10010, INF = 0x3f3f3f3f;

struct Edge {
    int a, b, w;
} edges[M];

int n, m, k;
int d[N];
int backup[N];

void bellman_ford() {
    memset(d, 0x3f, sizeof(d));
    d[1] = 0;

    for (int i = 0; i < k; i++) {
        memcpy(backup, d, sizeof(d));  // 备份，防止发生串联更新，若无法理解可参考01背包问题中的dp数组的更新顺序
        for (int j = 0; j < m; j++) {
            auto e = edges[j];
            d[e.b] = min(d[e.b], backup[e.a] + e.w);  // 松弛操作
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    cin >> n >> m >> k;

    for (int i = 0; i < m; i++) {
        int a, b, w;
        cin >> a >> b >> w;
        edges[i] = {a, b, w};
    }

    bellman_ford();

    if (d[n] > INF / 2) cout << "impossible\n";  // 可能会有负权边使得d[n]略小于INF，所以不能用d[n] == INF来判断
    else cout << d[n] << "\n";

    return 0;
}