欢迎来到 Claffic 的博客 💞💞💞
前言:
快慢指针指的是每次指针移动的步长,是解决链表相关的题目的一大利器,下面我将以例题的形式讲解快慢指针法。
目录
一. 链表的中间结点
思路:
代码实现:
二. 链表中倒数第k个结点
思路:
代码实现:
三. 判断链表中是否有环
思路:
代码实现:
四. 返回链表入环的第一个结点
思路:
代码实现:
一. 链表的中间结点
点我做题
思路:
创建两个快慢指针 slow , fast ,起始共同指向头节点,slow 每次走一步,fast 每次走两步,当 fast 为空或 fast 的下一个结点为空时,slow 即是中间节点的位置。
解释:
由于 fast 每次走两步,slow 每次走一步,slow 总是落后 fast 整体一半的长度最终 slow 理应为中间结点。
结点数为奇数:
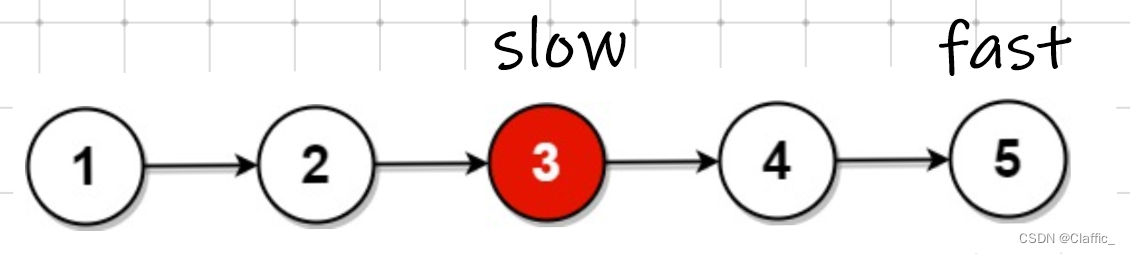
最终 fast 在最后一个结点,此时结束的标志为 fast->next == NULL;
结点数为偶数:

最终 fast 在最后一个结点的下一个指向,此时的结束标志为 fast == NULL;
代码实现:
struct ListNode* middleNode(struct ListNode* head){
struct ListNode* slow,*fast;
slow = head;
fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
}
return slow;
}二. 链表中倒数第k个结点
点我做题
思路:
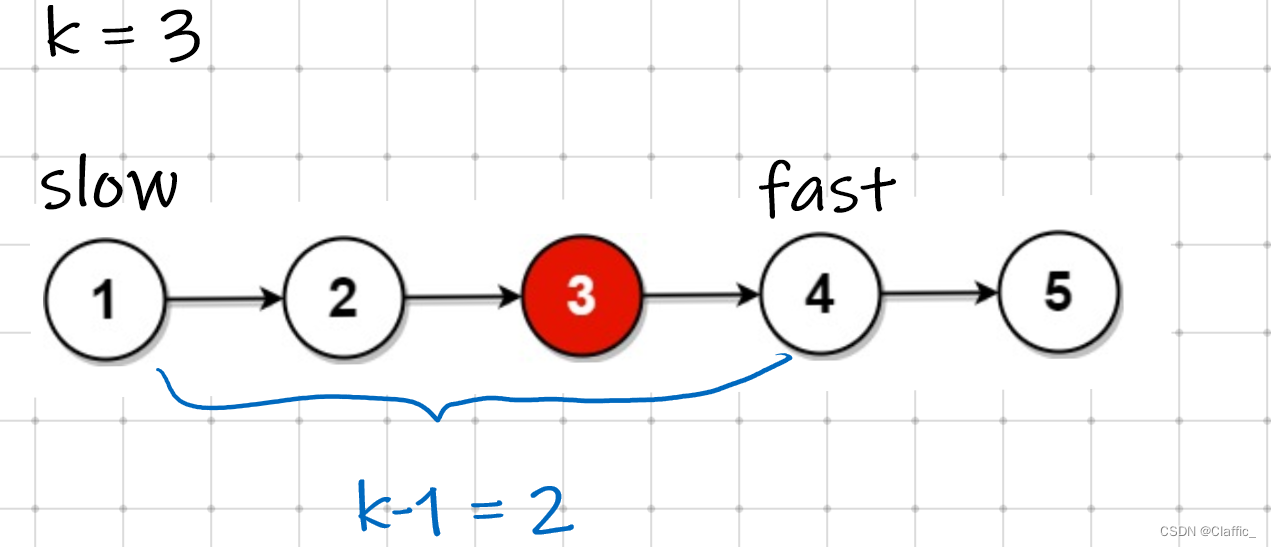
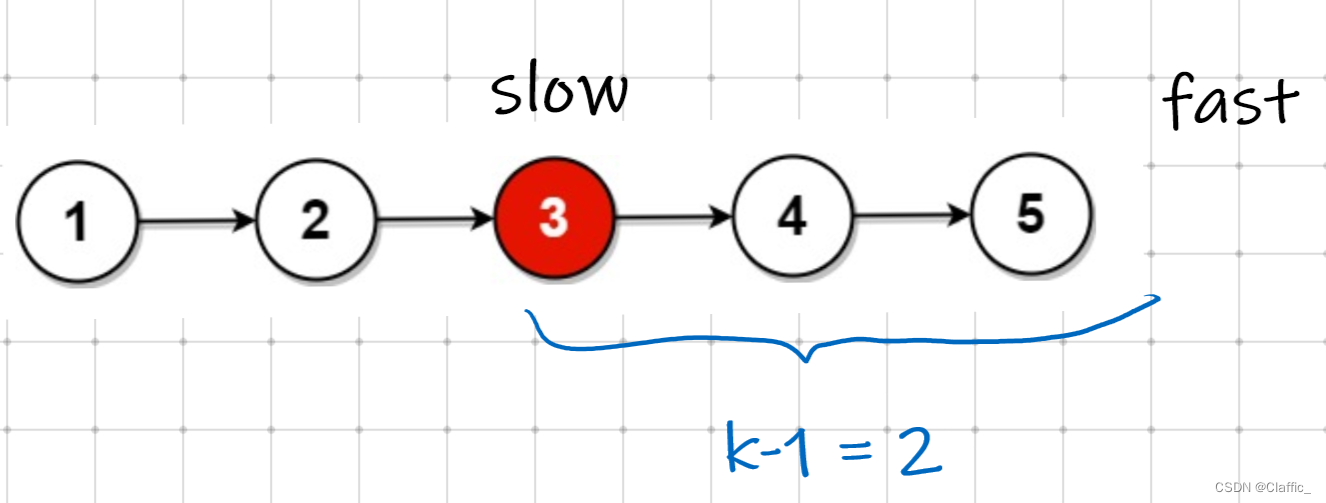
同样,创建两个快慢指针 slow , fast ,起始共同指向头节点,先让 fast 走 k 步,再让 fast 和 slow 同时前进,直到 fast 为空为止。
解释:
先让 fast 走 k 步,那么 fast 与 slow 之间就隔了 k-1 个结点,fast 与 slow 同时前进,直到 fast 为空时,fast 与 slow 之间依然隔 k-1 个结点,那就是倒数第 k 个结点。
代码实现:
int kthToLast(struct ListNode* head, int k){
struct ListNode* fast,*slow;
fast = slow = head;
if(head == NULL)
{
return NULL;
}
//fast 前进 k 步
while(k--)
{
fast = fast->next;
}
//slow 与 fast 共同前进
while(fast)
{
slow = slow->next;
fast = fast->next;
}
//注意返回的是整型数值
return slow->val;
}三. 判断链表中是否有环
点我做题
思路:
快慢指针 slow , fast,都从 head 开始,slow 一次走一步,fast 一次走两步,如果 slow 和 fast 能相遇,则链表有环。
解释:
主要是证明 有环情况下两个指针一定能相遇:
fast 比 slow 先进入环,如图,假设 slow 和 fast 的位置,这两个指针之间差 N 步,
由于 fast 每次走两步,slow 每次走一步,所以 slow 和 fast 之间的距离每次缩短 1

N - 1
N - 2
N - 3
...
2
1
0 //此时两者相遇
证毕。
代码实现:
bool hasCycle(struct ListNode* head) {
struct ListNode* fast,*slow;
fast = slow = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(fast == slow)
{
return true;
}
}
return false;
} 四. 返回链表入环的第一个结点
点我做题
思路:
这里要先放一个结论:
在链表有环的情况下,一个指针在起始结点开始走,另一个结点在相遇点开始走,最终两个指针会在入环点相遇。
快慢指针 slow , fast,都从 head 开始,slow 一次走一步,fast 一次走两步,找到相遇点后,再让 start 与 meet 同时前进,两者相等的点即是入环点。
解释:
自然要证明上边的结论:
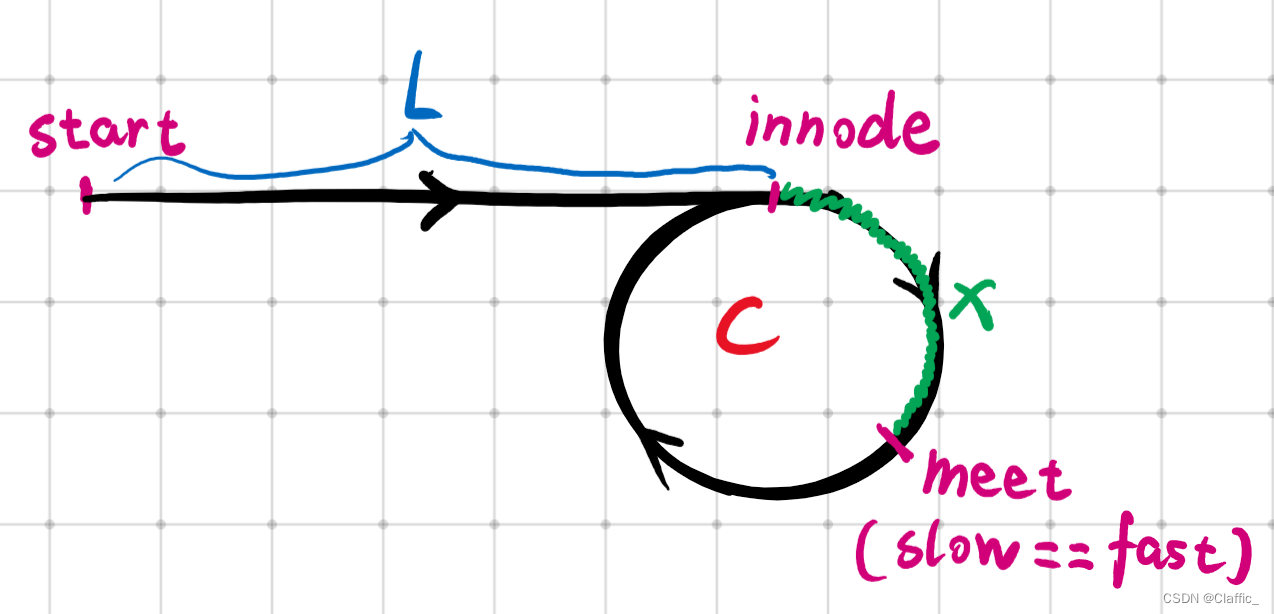
在这里,我们设几个常量:
L:起始点到入环点的距离;
X:入环点到相遇点的距离;
C:环的周长。
已知条件:
slow 走的距离:L + X ;
fast 走的距离:L + n*C + X (n >=1) ;
fast 走的长度是 slow 走的长度的 2 倍。
推导:
fast 走的长度是 slow 走的长度的 2 倍 -->
2*(L + X) == L + n*C + X (n >=1),
整理得:L == C - X + (n - 1)*C (n >=1).
对 L == C - X + (n - 1)*C (n >=1) 的解释:
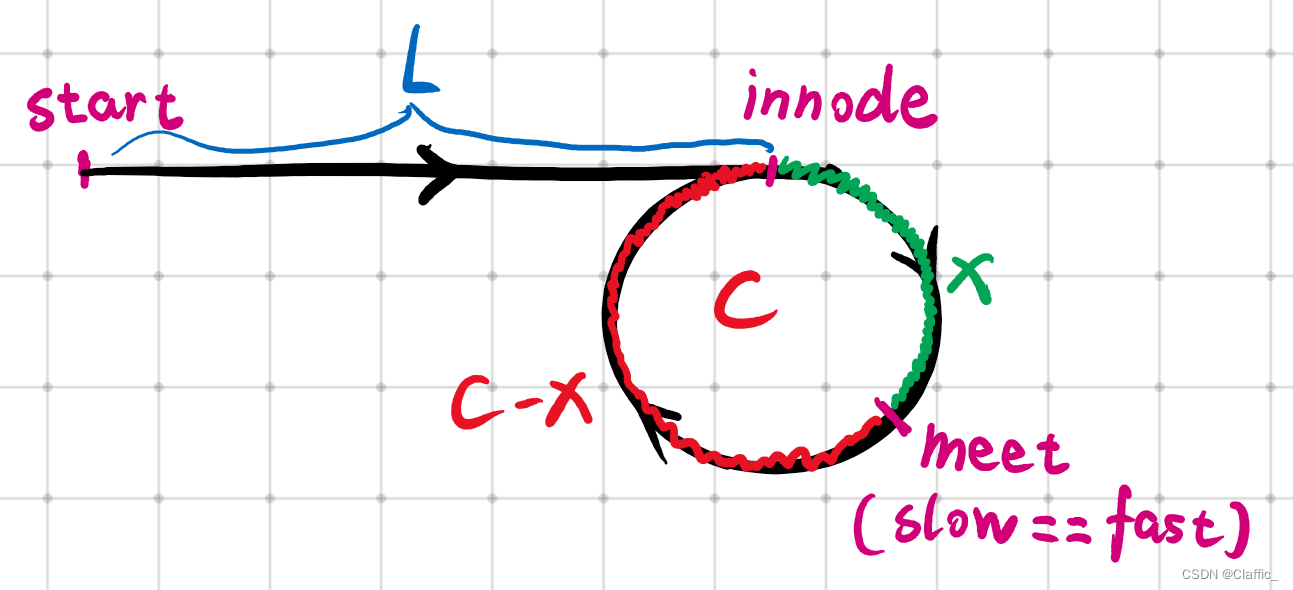
C - X + (n - 1)*C (n >=1) 原本是 meet 到 innode 要走的所有可能距离,
而 L == C - X + (n - 1)*C (n >=1) ,说明 start 到 innode 要走的距离与 meet 到 innode 要走的所有可能距离相等,所以两者相遇的点一定是 innode.
代码实现:
struct ListNode* detectCycle(struct ListNode *head) {
struct ListNode* slow,*fast;
slow = fast = head;
while(fast && fast->next)
{
slow = slow->next;
fast = fast->next->next;
if(slow == fast)
{
struct ListNode* meet = slow;
struct ListNode* start = head;
while(meet != start)
{
meet = meet->next;
start = start->next;
}
return meet;
}
}
return NULL;
}总结:
快慢指针是解决链表问题的一大利器,建议多画图理解掌握。
码文不易
如果你觉得这篇文章还不错并且对你有帮助,不妨支持一波哦 💗💗💗