给定一个长度为 n n n 的数组 a a a 和一个长度为 m m m 的数组 b b b。
两个数组均只包含 0 0 0 和 1 1 1。
利用两个给定数组生成一个 n × m n×m n×m 的矩阵 c c c,其中 c i j = a i × b j c_{ij}=a_i×b_j cij=ai×bj。
显然,矩阵 c c c 中也只包含 0 0 0 和 1 1 1。
请问,矩阵 c c c 中有多少个大小(面积)恰好为 k k k 且只包含 1 1 1 的子矩形?
子矩形是指矩阵中连续若干行和连续若干列的交集。
例如,考虑四个整数 x 1 , x 2 , y 1 , y 2 ( 1 ≤ x 1 ≤ x 2 ≤ n , 1 ≤ y 1 ≤ y 2 ≤ m ) x_1,x_2,y_1,y_2(1≤x_1≤x_2≤n,1≤y_1≤y_2≤m) x1,x2,y1,y2(1≤x1≤x2≤n,1≤y1≤y2≤m),子矩形 c [ x 1 … x 2 ] [ y 1 … y 2 ] c[x_1…x_2][y_1…y_2] c[x1…x2][y1…y2] 即为行 x 1 , x 1 + 1 , … , x 2 x_1,x_1+1,…,x_2 x1,x1+1,…,x2 和列 y 1 , y 1 + 1 , … , y 2 y_1,y_1+1,…,y_2 y1,y1+1,…,y2 的一个交集。
一个子矩形的大小(面积)等于它包含的数字个数。
输入格式
第一行包含三个整数
n
,
m
,
k
n,m,k
n,m,k。
第二行包含 n n n 个整数 a 1 , … , a n a_1,…,a_n a1,…,an,表示数组 a a a 中的元素。
第三行包含 m m m 个整数 b 1 , … , b m b_1,…,b_m b1,…,bm,表示数组 b b b 中的元素。
输出格式
输出满足条件的子矩形的总数量。
数据范围
1
≤
n
,
m
≤
40000
,
1≤n,m≤40000,
1≤n,m≤40000,
1
≤
k
≤
n
×
m
,
1≤k≤n×m,
1≤k≤n×m,
0
≤
a
i
,
b
i
≤
1
0≤a_i,b_i≤1
0≤ai,bi≤1
输入样例1:
3 3 2
1 0 1
1 1 1
输出样例1:
4
输入样例2:
3 5 4
1 1 1
1 1 1 1 1
输出样例2:
14
样例解释
对于样例
1
1
1,矩阵
c
c
c 如下:
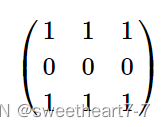
共有 4 个面积为 2 且只包含 1 的子矩形,如下:
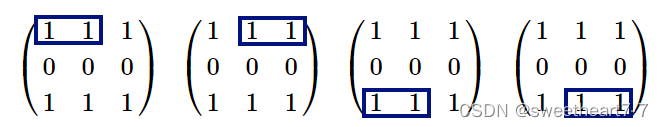
对于样例 2,矩形 c 如下:
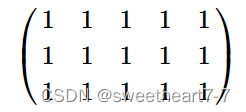
- 矩形面积为 k k k,可以枚举一个边 ( a , b ) (a, b) (a,b)
- 可以发现求面积为 k k k 的 1 1 1 的矩形个数,相当于求 ( A A A 中有多少个连续的 1 1 1 长度为 a a a) ✖ ( B B B 中有多少个连续的 1 1 1 长度为 b b b)
- 用 s s s 数组距离长度为 i i i 的 1 1 1 的个数, s [ i ] s[i] s[i] 表示有 s [ i ] s[i] s[i] 个(连续的 1 1 1)长度为 i i i
- 当 A A A 中有连续的 1 1 1 长度为 t t t,它对 s s s 数组 [ 1 [1 [1~ t ] t] t] 都有个为 1 1 1 的贡献(相当于给 s [ 1 s[1 s[1~ t ] t] t] 都加{可以用差分数组处理})
#include<iostream>
using namespace std;
typedef long long LL;
const int N = 40010;
int n, m, k;
int a[N], b[N];
int s1[N], s2[N];
void work(int w[], int s[], int n){
int j = 0;
for(int i = 0; i < n; i++)
if(w[i] == 1){
j++;
s[1]++;
s[j + 1]--;
}else j = 0;
for(int i = 1; i <= n; i++) s[i] += s[i-1];
}
int main(){
scanf("%d%d%d", &n, &m, &k);
for(int i = 0; i < n; i++) scanf("%d", &a[i]);
for(int i = 0; i < m; i++) scanf("%d", &b[i]);
work(a, s1, n);
work(b, s2, m);
LL res = 0;
for(int i = 1; i <= n; i++){
if(k % i) continue;
int j = k / i;
if(j > m) continue;
res += s1[i] * s2[j];
}
printf("%lld\n", res);
return 0;
}