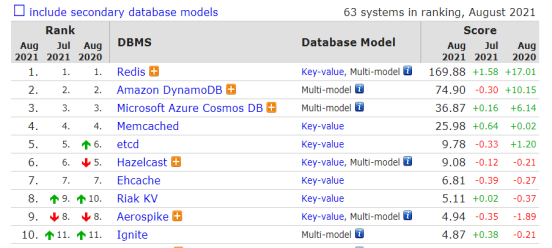
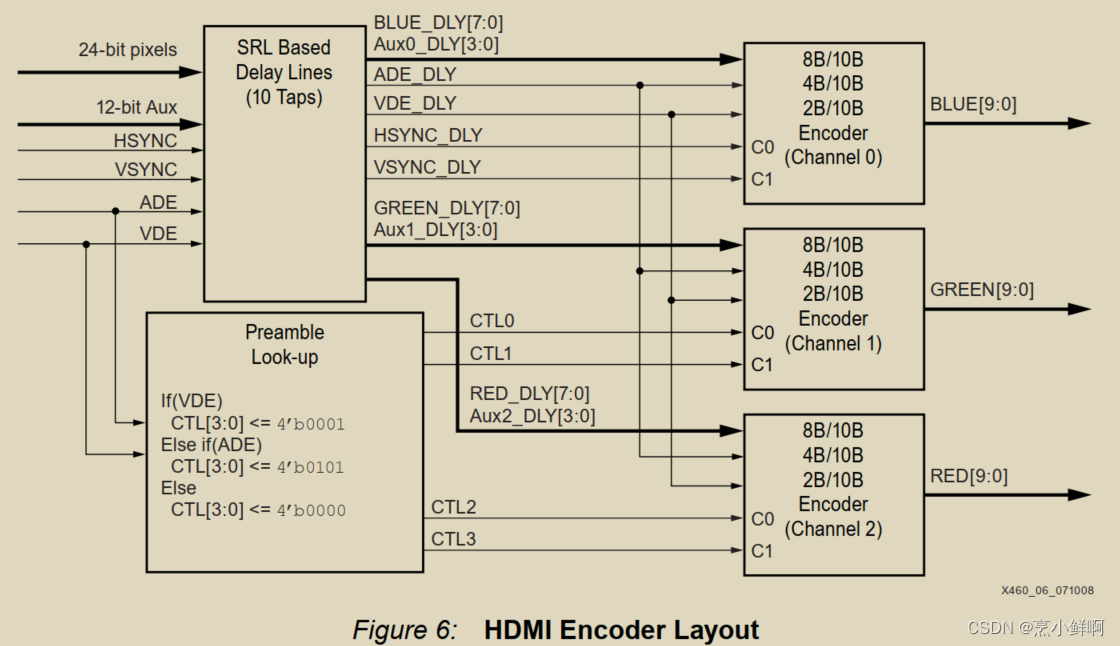
题目

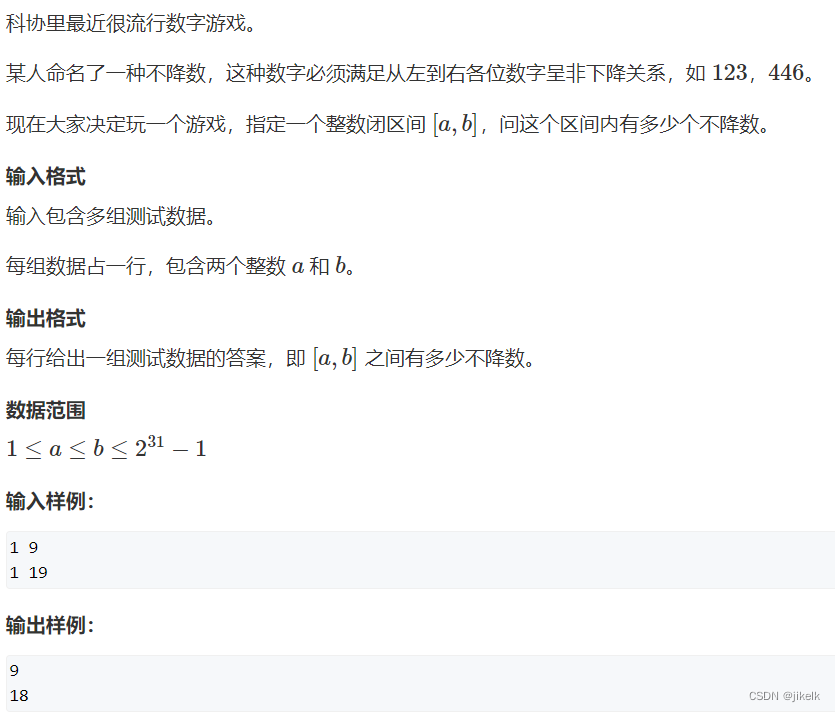
思路
也是一道比较典型的数位dp的问题，关键的思想跟我上一篇博客很像，
首先把区间值变成[1,Y]-[1,X-1]的值，然后单独计算得到结果。
总的来说就是把这个数的每一位都单独拿出来，然后根据选0-a_n-1和选**a_n**两种方案单独计算：

当选第一种方案时，就是后面的i位**（因为最低为从a₀开始）的数字可以任意选，那么就可以表示为前面的最高位为last**，一共i+1位的决策数。

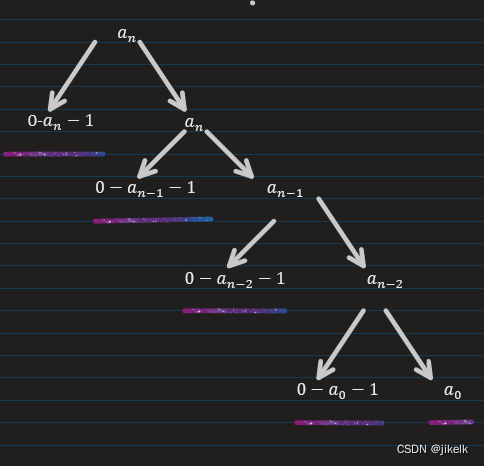
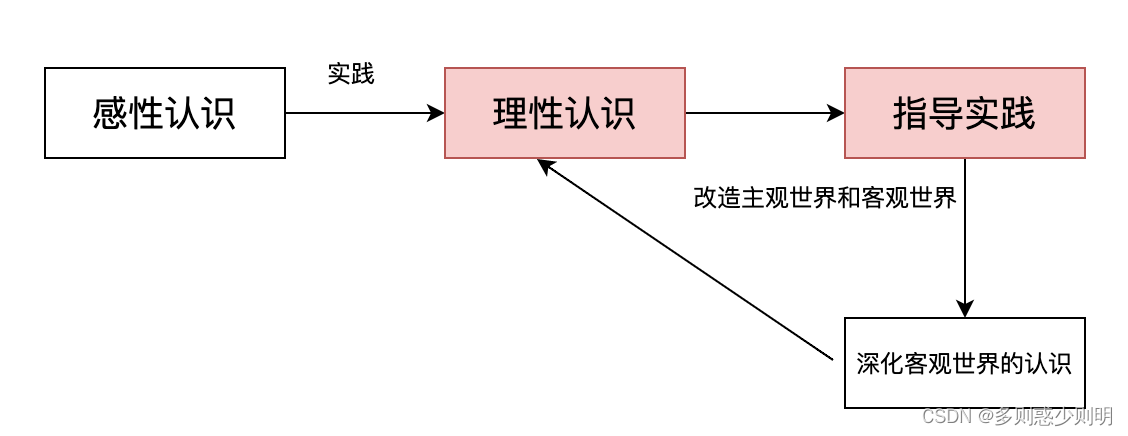
ps：上一篇博客的图（

那么这里求决策数就需要用到动态规划了。
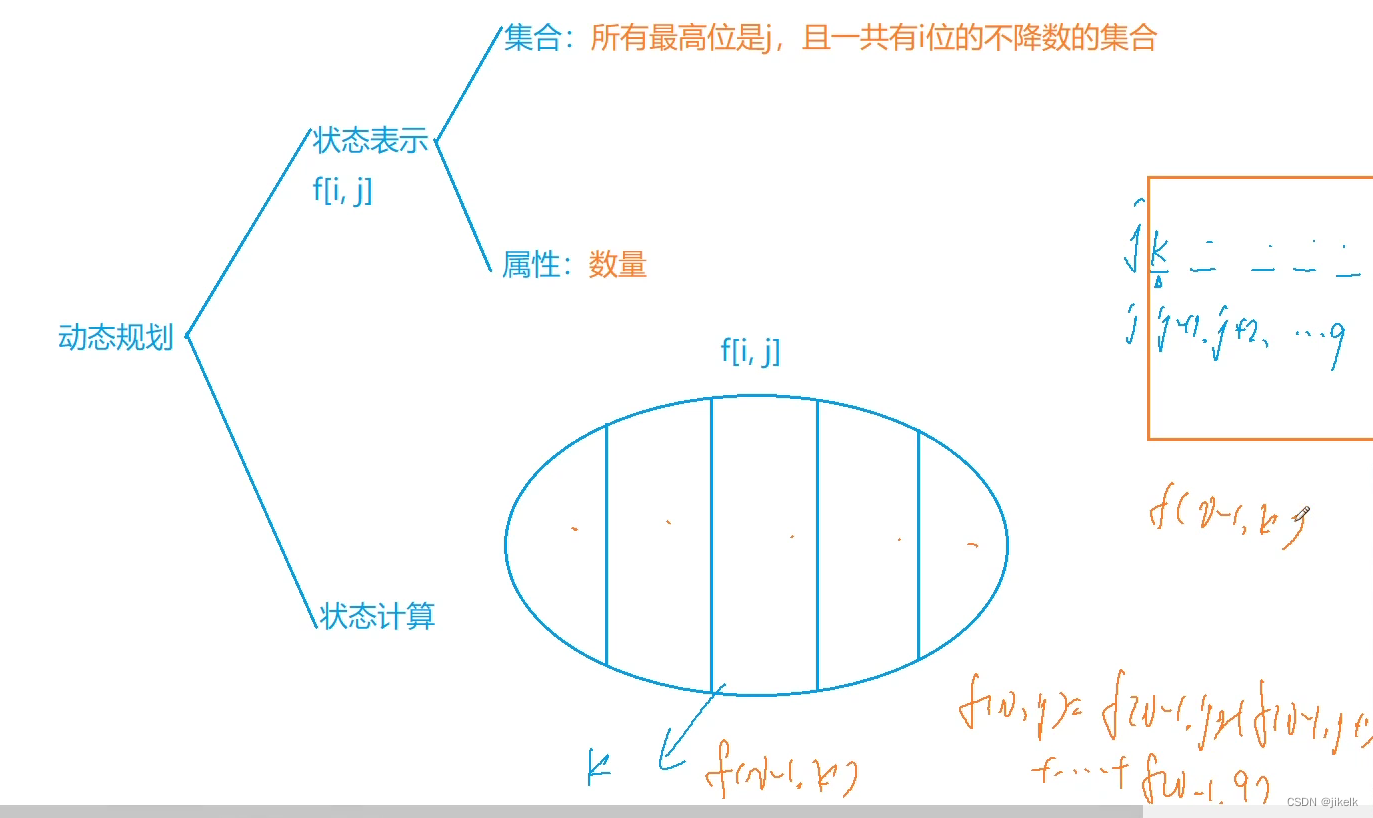
这里用f[i][j]表示前面的最高位为j，并且一共有i位的不降数的集合，
那么f[i][j]肯定要从前面的状态中得到，那么在第i位为j的时候，
i-1位的选择可以为 j , j + 1 , j + 2 ，… ， 9这些情况，
这些情况之和就相当于f[ i ] [ j ] , 那么f [ i ] [ j ]就可以表示为f[ i -1] [ j ]+f [ i-1 ] [ j + 1 ]+…+f [ i -1] [ 9 ]。这里可以预处理获得所有情况的f[ i ] [ j ]，这样上面的方案数就可以直接算出来了（这里借用了y总的图片一用）

当选第二种方案时
即要选择当前位的最大值时，要进行特判，即上一位的最大值是不是小于当前位的最大值的，（即last<x）如果不满足则不能走到下一位直接返回，如果满足则直接进行最大值的覆盖。然后走到最右下角的决策时如果还是能选到a₀，那么就作为一种方案数使res++，然后返回res即可。

具体代码

#include<cstdio>
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include<vector>
#include<queue>
#include<map>
#define sc_int(x) scanf("%d", &x)
#define sc_ll(x) scanf("%lld", &x)
#define pr_ll(x) printf("%lld", x)
#define pr_ll_n(x) printf("%lld\n", x)
#define pr_int_n(x) printf("%d\n", x)
#define ll long long 
using namespace std;

const int N=20;
int n ,m,h;
int s[N][N];


void cal()
{
	for(int i =0;i<=9;i++)s[1][j]=1;

	for(int i =1;i<=N;i++)
		for(int j =0;j<=9;j++)
			for(int k=j;k<=9;k++)
			s[i][j]+=s[i-1][k];
}

int dp(int n)
{
	if(!n) return 1;//特判，如果为0也可以作为一种决策

	vector<int>cnt;
	while(n)cnt.push_back(n%10),n/=10;

	int res=0;
	int last=0;
	for(int i =cnt.size()-1;i>=0;i--)
	{
		int x=cnt[i];
		for(int j =last;j<x;j++)
		res+=s[i+1][j];

		if(last>x)break;
		x=last;
		
		if(!i)res++;
	}
	return res;
}	

int main()
{
	int t;
	cal();
	int l,r;
	while(cin>>l>>r)
	cout<<dp(r)-dp(l-1)<<endl;
	
	return 0;
}

ps：作为数位dp的第二篇，感觉理解起来容易了很多（最不好理解的点还是方案数的预处理哪里），希望以后的数位dp能越学越熟悉吧。