一、电话号码的字母组合

题目链接

思路：回溯三部曲。

• 确定回溯函数参数：题目中给的 digits，还要有一个参数就是int型的index（记录遍历第几个数字，就是用来遍历digits的，同时也代表了递归的深度），第三个参数numString(数字和字母映射)。

• 确定终止条件：如果index 等于 输入的数字个数（digits.size）了，就return。

• 确定单层遍历逻辑：首先要取index指向的数字，并找到对应的字符集；然后for循环来处理这个字符集

注意：

（1）解决三个问题

• 数字和字母如何映射 （使用map或者定义一个二维数组）

• 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来

• 输入1 * #按键等等异常情况

（2）区别于普通的组合问题，本题是多个集合求组合，因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合。

（3）全局变量：一个字符串sb来收集叶子节点的结果，一个字符串数组result保存sb。

解法：

class Solution {
    // 最终结果字符数组和单次符合条件结果
    List<String> res = new ArrayList<>();
    StringBuffer sb = new StringBuffer();

    public List<String> letterCombinations(String digits) {

        if (digits.length() == 0 || digits == null)
            return res;
        String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
        backTracking(digits, numString, 0);
        return res;
    }

    public void backTracking(String digits, String[] numString ,int num) {
        if (num == digits.length()){
            res.add(sb.toString());
            return;
        }
        // digits.charAt(num)能够获取到当前的号码数字，2-9
        String t = numString[digits.charAt(num) - '0'];
        for (int i = 0; i < t.length(); i++) {
            sb.append(t.charAt(i));
            backTracking(digits, numString, num + 1);
            sb.deleteCharAt(sb.length() - 1);  //回溯
        }
    }
}

二、组合总和

题目链接

思路：基本与组合总和III类似。区别有：

• 组合没有数量要求

• 元素可无限重复选取

注意：

• 如果是一个集合来求组合的话，就需要startIndex；（否则会出现重复情况）

• 如果是多个集合取组合，各个集合之间相互不影响，那么就不用startIndex。

解法（未剪枝）：

List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {
    // sum,   startIndex是开始位置也是candidates的索引
    back(candidates, target, 0,0);
    return res;
}

private void back(int[] candidates, int target, int sum, int startIndex) {

    if (sum == target){
        res.add(new ArrayList<>(path));
        return;
    }
    if (sum > target)
        return;
    for (int i = startIndex; i < candidates.length; i++){
        path.add(candidates[i]);
        sum += candidates[i];
        back(candidates, target, sum, i);
        sum -= candidates[i];
        path.removeLast();
    }
}

剪枝优化：

1.对总集合排序之后，如果下一层的sum（就是本层的 sum + candidates[i]）已经大于target，就可以结束本轮for循环的遍历。

解法：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {

        Arrays.sort(candidates); // 先进行排序
        back(candidates, target, 0,  0);
        return res;
    }

    private void back(int[] candidates, int target, int sum, int startIndex) {

        if (sum == target){
            res.add(new ArrayList<>(path));
            return;
        }
        if (sum > target)
            return;
        // 多一步判断
        for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){
            path.add(candidates[i]);
            sum += candidates[i];
            back(candidates, target, sum, i);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}

三、组合总和II

题目链接

思路：与组合总和类似，但区别于

1. 本题candidates 中的每个数字在每个组合中只能使用一次。

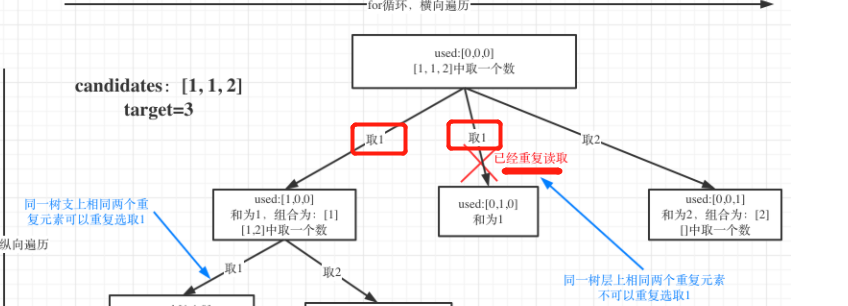
2. 本题数组candidates的元素是有重复的，而39.组合总和 (opens new window)是无重复元素的数组candidates。也就是说组合里的元素可能有重复且只使用一次，但组合之间不能重复。

3. 本题的难点在于区别2中：集合（数组candidates）有重复元素，但还不能有重复的组合。

4. 去重也去的是同一个树层上，重复的值。代码里就是判断i > startIndex && candidates[i] == candidates[i - 1]，直接continue

解法：

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates); // 先进行排序
        back(candidates, target, 0,  0);
        return res;
    }

    private void back(int[] candidates, int target, int sum, int startIndex) {

        if (sum == target){
            res.add(new ArrayList<>(path));
            return;
        }
        if (sum > target)
            return;
        for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){
            // 碰到同一树层重复元素  直接continue
            if ( i > startIndex && candidates[i] == candidates[i - 1] ) {
                continue;
            }
            path.add(candidates[i]);
            sum += candidates[i];
            back(candidates, target, sum, i + 1);
            sum -= candidates[i];
            path.removeLast();
        }
    }
}