1. 简介

在逻辑综合中，香农分解（Shannon decomposition）是一种常用的布尔函数分解方法。它将一个布尔函数分解为两个子函数的和，其中每个子函数包含一个布尔变量的取反和非取反的部分。

具体来说，假设对于一个布尔函数 $$F(x_1,x_2,...,x_n)$$

进行香农分解，首先选定进行分解的变量，假设为$x_k$，则该香农分解可以表示为：

$$\begin{gathered} F(x_1,x_2,...,x_n)= \\ {x}_k\ast F_k(x_1,x_2,...,x_n,x_k=1)+x_k^{\prime }\ast F_k^{\prime }(x_1,x_2,...,x_n,x_k=0) \end{gathered}$$
其中，$x_k$ 是函数 $F$ 的一个输入变量，$x_k^{\prime }$ 是 $x_k$ 的取反，$F_k$ 是当 $x_k=1$ 时 $F$ 的取值为真时的部分函数，$F_k^{\prime }$ 是当 $x_k=0$ 时 $F$ 的取值为真时的部分函数。

这个分解的意义在于，它将一个布尔函数 $F$ 分解成了两个子函数 $F_k$ 和 $F_k^{\prime }$，这两个子函数相互独立，因为它们只与 $F$ 的一个输入变量 $x_k$ 有关。这种分解可以用于减少门电路的复杂度，从而实现更快的逻辑运算和更小的电路面积，如何拿到更小的面积，后续了解到了再补充，本文主要是得到更快的速度。

香农分解的基本思想可以进一步扩展到多个输入变量的情况，即将一个布尔函数 $F(x_1,x_2,...,x_n)$ 分解成两个子函数 F0 和 F1，其中 F0 和 F1 分别只与 $x_1$ 取 0 和 1 时的输入变量 $x_2,x_3,...,x_n$ 有关。这种扩展的香农分解方法被称为递归香农分解（Recursive Shannon Decomposition），在实际的逻辑综合和电路设计中得到了广泛的应用。

2. 示例

假设有一个函数：
$$F=(a,b,c,x)$$
以变量 $x$ 进行分解，则可以得到以下表达式：
$$F=x.(a,b,c,1)+x\prime .F(a,b,c,0)$$
如果用电路图来表示以上分解的话，如下所示：

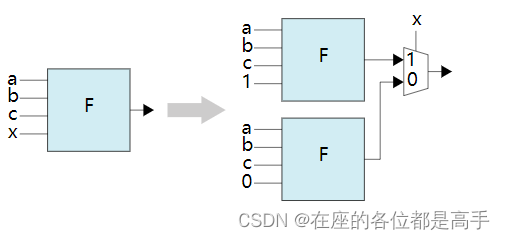
更近一步，常数的信号通常可以被优化掉，变成以下的结构：

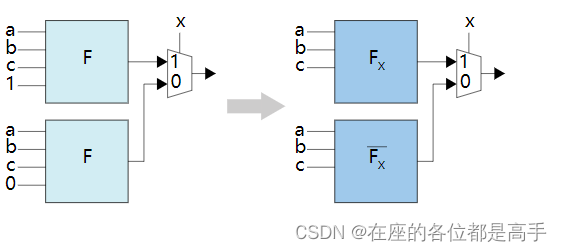
我们可以看到，经过香农分解后，信号 $x$ 距离输出 $output$ 最近，$x$ 所在的路径是整个 logic cone 中最快的一条。

所以说如果在电路 output required time 确定的情况下，某一个信号的 arrival time 非常的晚，可以把这个信号向靠近output的方向 push，从而降低电路的延迟。

这种做法的缺点也是显而易见的，至少在这个例子中，面积几乎一直出于增长的状态。

按照上面简介部分介绍的递归香农分解继续执行的话，可以得到如下电路：

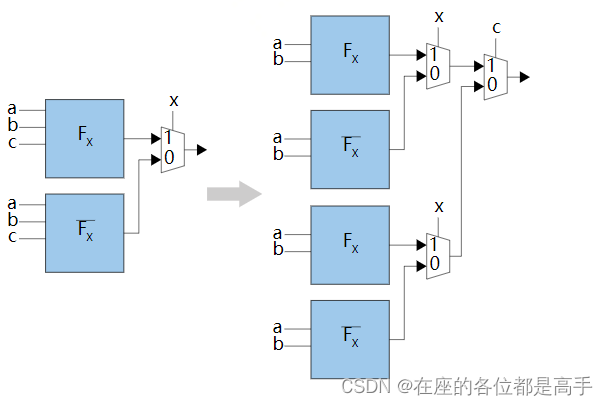
2.1 个人理解

做timing优化的时候主要是将那些 arrival time 比较慢的信号尽可能的往 output 推，所以也就是说要基于这些 arrival time慢的信号进行香农分解。

3. 特殊案例(pipeline loop)

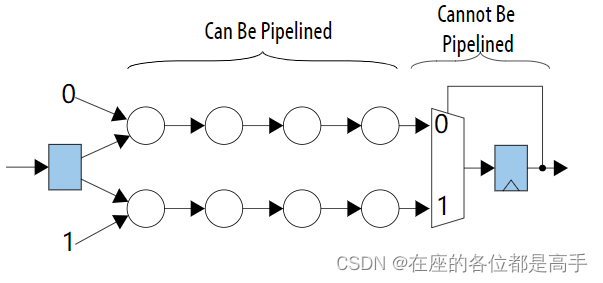
香农分解是优化电路中 $loop$ 的一种有效技术。当你对 $loop$ 中的逻辑执行香农分解时，$loop$ 中的逻辑会移动到 $loop$ 外部。从而可以对移动到循环外部的逻辑进行 $pipeline$ 处理。

假设有以下一个 $loop$ 电路，因为是在一个 $loop$ 里面，所以这一部分信号不能进行 $pipeline$：

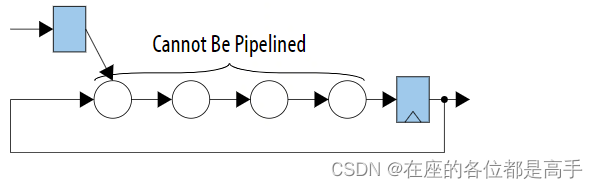
该电路有一个单独的 $register$ 和一个额外的输出，我们可以通过执行香农分解将这个 $loop$ 的逻辑移动到外部以进行 $pipeline$，具体的做法如下：

我们知道 $register$ $output$的值只能为 0 或者 1，所以我们可以将驱动 $register$ 的逻辑复制（duplicate）一份，一份 $register$ 的输入为 $0$， 一份为 $1$，即对于这个$output$ 进行香农分解，即可得到以下的电路：