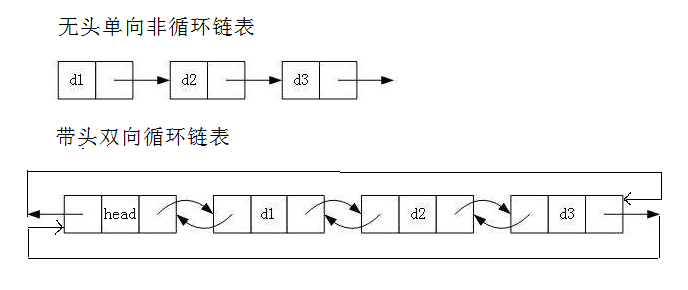
经验贝叶斯估计

贝叶斯估计的问题定义为根据一些观测数据 x 来估计未知参数 θ，用一个损失函数来衡量估计的准确性，如果用均方误差(MSE)来估计的话，将问题建模为

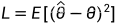
等价于求解后验分布的均值

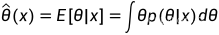
最小均方误差估计器 minimum mean square error (MMSE) estimator

上式中需要知道后验概率p(θ|x)，它是利用贝叶斯定理求出来的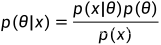，因此需要先知道似然函数p(x|θ)以及先验分布p(θ)

在此之前，经典贝叶斯参数估计中，有一组观察样本,是从条件概率密度为p(x|θ)的分布中采样出来的，在已知先验 p(θ) 参数的前提下，估计目标参数。

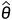但是经验贝叶斯 (Empirical Bayes)里，先验分布的参数是没有提前给定的，也是要通过观测数据去估计。

经验贝叶斯方法可以被看成是分层贝叶斯模型：在一个两阶段的分层贝叶斯模型中，观测数据是从一组未知的参数 中根据 p(x|θ)生成的，注意每一个样本

只对应参数 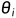，不像经典贝叶斯估计，对于一个参数有多个观测数据，而是对于一个参数只有一个观测数据；

θ是从 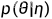中获取的，其中 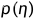是非参数的分布，也可以直接表示为 p(θ)。目标是估计

以一个高斯分布为例，先从分布 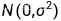采样一组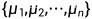,再分别从分布中采样一个，构成一组观测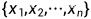,相当于二次采样

另一种理解的方式是将它看成是一个多元混合分布呢，采样一个样本，但它有多个维度，每个维度是服从一个分布的，所以不同维度就服从不同的分布。

如果要统一起来，方便符号表示的话，记单一样本为 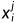，下标表示是第几维，上标表示是这一维的第几次采样。

利用最大似然估计，很容易得知 ，因为对于待估计的参数 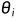只有一个观测样本。而如果有更多m个观测样本 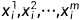则会估计得更准确。

直观理解就是：经验贝叶斯需要用到辅助的经验信息，待估计参数可以通过其他相关参数进行辅助（因为这些参数是从相同的先验形式），而其他相关参数又是可以通过其他观测数据获得的，这样就可以使用来自其他观测数据来改进特定参数的估计性能。

Robbins Estimator (罗宾斯估计)

根据经验贝叶斯估计定义，在泊松分布下: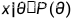

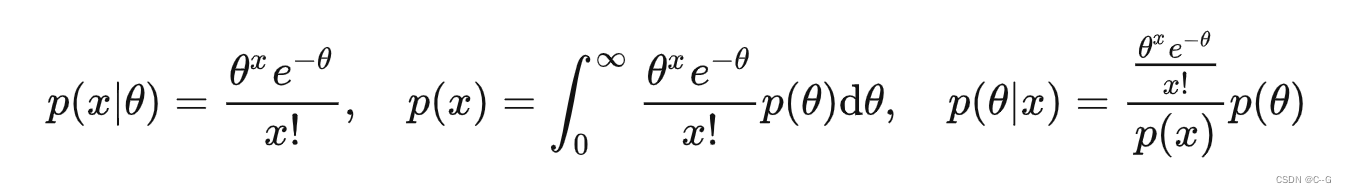
后验的期望

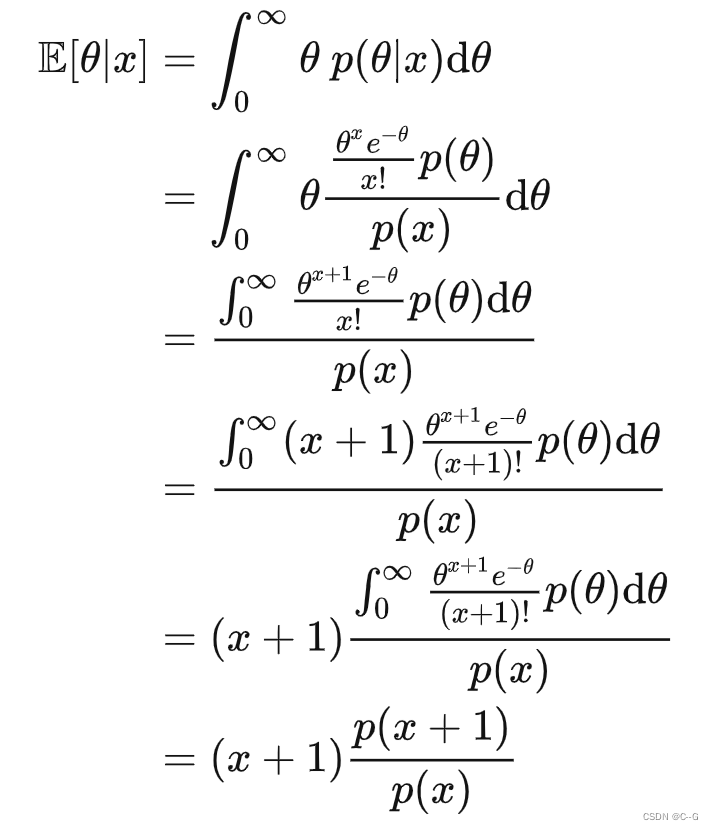
对于边缘分布 p(x) 可以用 x 出现的频率来估计，如果知道对应取值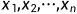的出现频次分别为 那么

最终得到了罗宾斯估计结果，而要用到这个结论，需要知道事件发生的频次，而且目标项只增加后一项对它的信息增强，如果目标项是最后一项其实也是无能为力的。

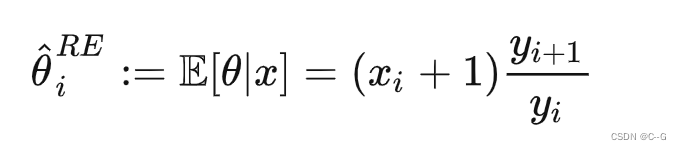
James-Stein Estimator (詹姆斯坦估计)

罗宾斯估计中是针对泊松分布进行的研究，詹姆斯坦估计则是针对高斯分布进行的研究。我们先假设一个简单的例子，其中 θ 是未知的，σ 是已知的：

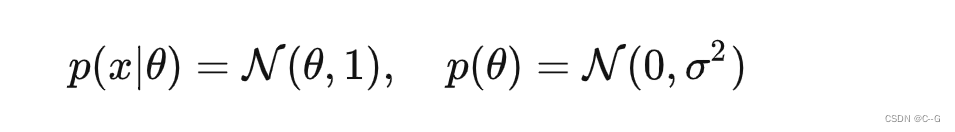
先要写出 x 的边缘分布

积分部分的推导是利用了 Gaussian intergral 的一个结论

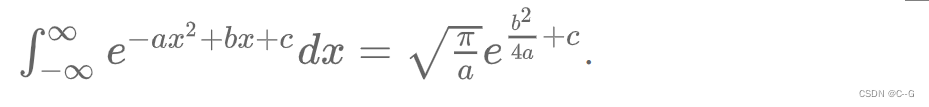
也是一个高斯分布，意味着 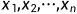是从分布 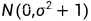中采样得到的，且与先验分布的参数无关。 同时可以通过这些观测样本来估计先验分布的参数 (n-1来自于无偏估计)：

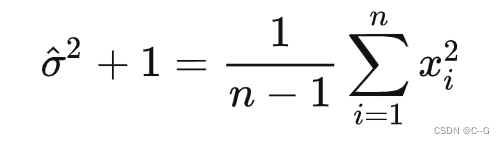
进一步推导后验分布

后验的期望就可以表示为

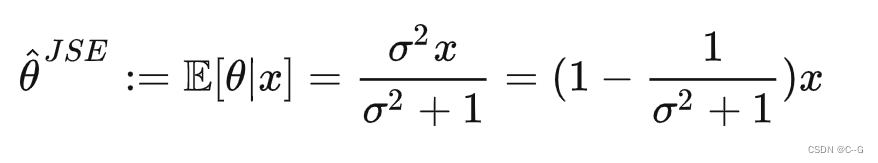
上述期望的含义是估计在观测样本下参数的值。对于一个具体的观测样本 和它对应的参数 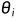，并代入下式其他样本的估计

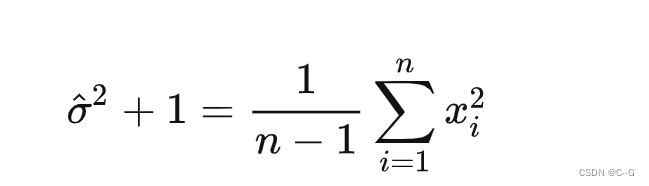
可以写出

相较于罗宾斯估计只用到一个相关观测，詹姆斯坦估计用到了所有观测量