最近看论文看到深度卷积的内容，然后就想着学习一下，发现论文中说的深度卷积并不是真正的深度卷积，感觉是分组卷积的一种，但是对于论文中得使用方式又有点不理解，就留下了一个问题放在了博客的最后，这里记录一下，方便以后查阅。

常规卷积

下图以stride=1，padding=0，kernel_size=3为例，假设输入特征图大小是4x4的（假设输入输出都是单通道），通过卷积后得到的特征图大小为2x2。一般使用卷积的情况中，要么特征图变小（stride > 1），要么保持不变（stride = 1），当然也可以通过四周padding让特征图变大但没有意义。

常规卷积中，连接的上一层一般具有多个通道（这里假设为n个通道），因此在做卷积时，一个滤波器（filter）必须具有n个卷积核（kernel）来与之对应。一个滤波器完成一次卷积，实际上是多个卷积核与上一层对应通道的特征图进行卷积后，再进行相加，从而输出下一层的一个通道特征图。在下一层中，若需要得到多个通道的特征图（这里假设为m个通道），那么对应的滤波器就需要m个。

用通俗的话来概括卷积，他起到的作用就是两个：一个是对上一层的特征图进行尺寸调整，另一个是则是对上一层的特征图数量进行调整，也就是通道数的调整。

看了上面这张图突然发现跟我最近理解的有点出入，最近都把卷及操作想成了下面“组卷积”图中的左边的样子，也就是前面一列是输入通道，后面一列是这一层卷积的卷积核数量，但是今天研究“深度卷积”，看到了torch.nn.Conv2d的解释中的下面图片的内容，起初还有点不理解权重的第二维是啥，但是现在结合上面的图和下面的图的解释就很明白了。

也就是，卷积层的权重通常被表示为一个四维张量，其形状为 （输出通道数，输入通道数，卷积核高度，卷积核宽度）。

分组卷积

Group Convolution（AlexNet），对输入进行分组，卷积核数量不变，但输入channel数$M$减少，相当于
$$M\to \frac{M}{G}$$

大卷积核替换为多个堆叠的小核

大卷积核替换为多个堆叠的小核（VGG），比如$5\times 5$替换为2个$3\times 3$，$7\times 7$替换为3个$3\times 3$，保持感受野不变的同时，减少参数量和计算量，相当于把 大数乘积 变成 小数乘积之和
$$(K\times K)\to (k\times k+\cdots +k\times k)$$

Factorized Convolution

Factorized Convolution（Inception V2），二维卷积变为行列分别卷积，先行卷积再列卷积
$$(K\times K)\to (K\times 1+1\times K)$$

Depthwise Convolution

Depthwise Convolution其实就是分组卷积的分组数跟input_features的channel数一样的时候，然后一个卷积核负责一个通道，一个通道只被一个卷积核卷积（拿分组卷积中的例子来说的话，就是分为12组）。

Depthwise Convolution完成后的Feature map数量与输入层的通道数相同，无法扩展Feature map。而且这种运算对输入层的每个通道独立进行卷积运算，没有有效的利用不同通道在相同空间位置上的feature信息。因此需要Pointwise Convolution来将这些Feature map进行组合生成新的Feature map。

Pointwise Convolution

Pointwise Convolution中的kernel[K, N, 1, 1]， 这里K的大小跟上一层的通道数是一致的，实现了深度方向的加权组合。

Depthwise Separable Convolution

Depthwise Separable Convolution（MobileNet V1），depthwise +BN ReLU + pointwise + BN ReLU，相当于将channel维单独分解出去，
$$(K\times K\times N)\to (K\times K+N)$$

Separable Convolution

Separable Convolution（Xception），pointwise + depthwise + BN ReLU，也相当于将channel维分解出去，但前后顺序不同（但因为是连续堆叠，其实跟基本Depthwise Separable Convolution等价），同时移除了两者间的ReLU
$$(K\times K\times M)\to (M+K\times K)$$
但实际在实现时还是depthwise + pointwise + ReLU

膨胀卷积

膨胀卷积在标准卷积的基础上，增加一些空洞，使得在卷积时能够包括更大的感受野。

转置卷积

转置卷积主要作用就是起到上采样的作用。但转置卷积不是卷积的逆运算（一般卷积操作是不可逆的），它只能恢复到原来的大小（shape）数值与原来不同。转置卷积的运算步骤可以归为以下几步：

• 在输入特征图元素间填充s-1行、列0（其中s表示转置卷积的步距）
• 在输入特征图四周填充k-p-1行、列0（其中k表示转置卷积的kernel_size大小，p为转置卷积的padding，注意这里的padding和卷积操作中有些不同）
• 将卷积核参数上下、左右翻转
• 做正常卷积运算（填充0，步距1）

下面假设输入的特征图大小为2x2（假设输入输出都为单通道），通过转置卷积后得到4x4大小的特征图。这里使用的转置卷积核大小为k=3，stride=1，padding=0的情况（忽略偏执bias）。

• 首先在元素间填充s-1=0行、列0（等于0不用填充）
• 然后在特征图四周填充k-p-1=2行、列0
• 接着对卷积核参数进行上下、左右翻转
• 最后做正常卷积（填充0，步距1）

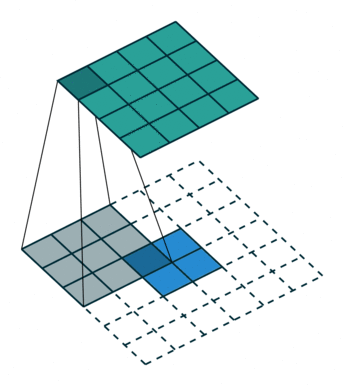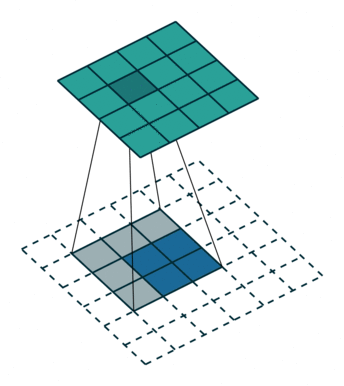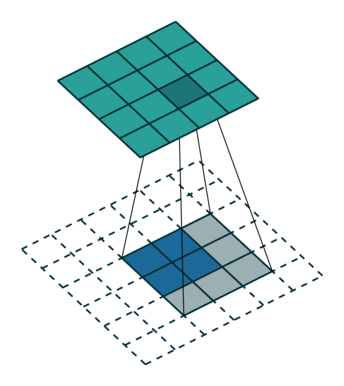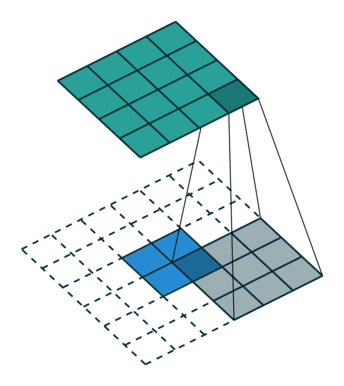
下图展示了转置卷积中不同s和p的情况：

s=1, p=0, k=3	s=2, p=0, k=3	s=2, p=1, k=3

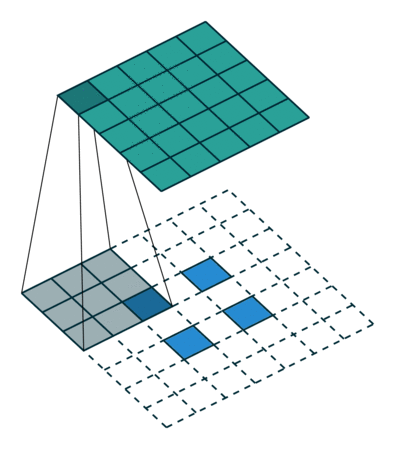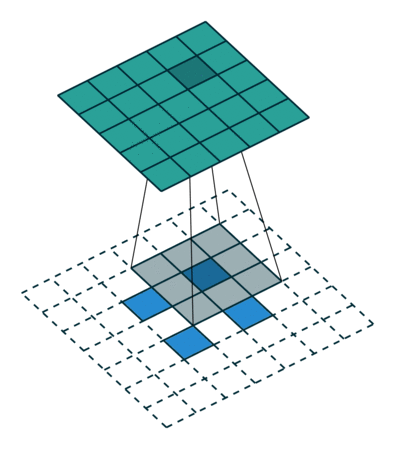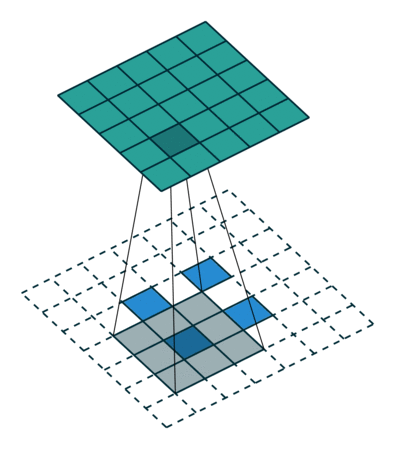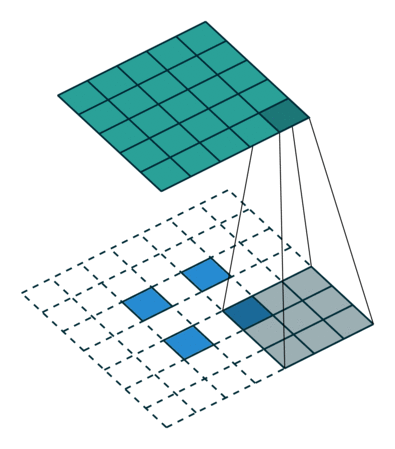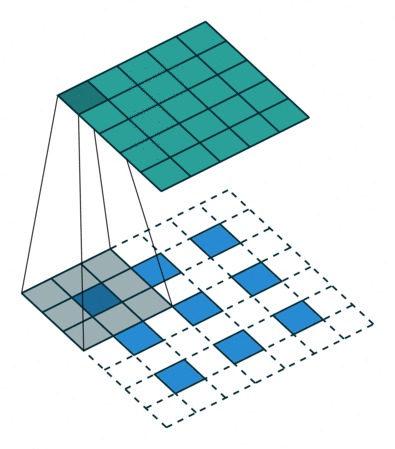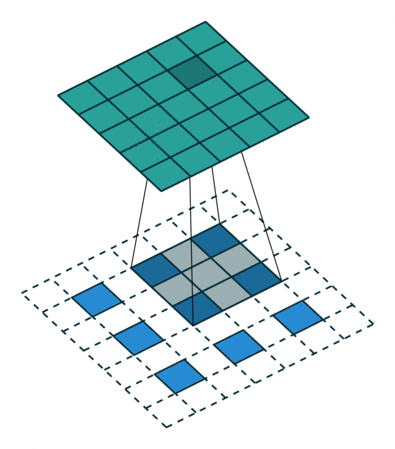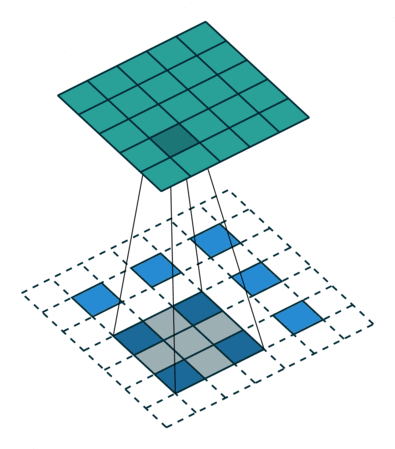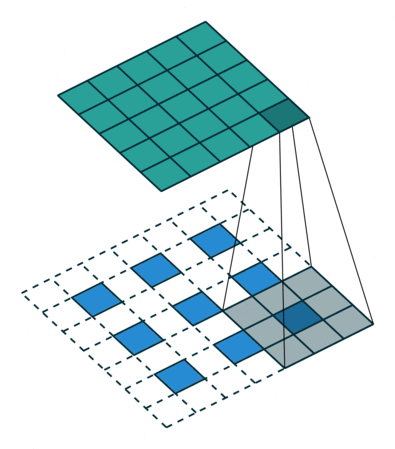问题

如果Group Convolution中，输入通道为8，输出通道为32，组数与输入通道数相等，则Group Convolution中权重的尺寸为（32,1，kernel_H，kernel_L）那么32个卷积核中哪四个是一组的？

我猜测是前四个一组然后依次类推，但是没有找到确实的证据证明这一点，去看pytorch的源代码也没有找到相关的内容，如果有大佬知道，还请在评论区留言，谢谢。

有个需要注意的点就是，当给卷积层的“groups”赋值之后，对于卷积的层的输出通道就有了要求，它要求输出通道数必须是groups的整数倍，在pytorch的源代码中是这样写的：

所以说，我的猜测还是有可能的！

参考资料

从卷积拆分和分组的角度看CNN模型的演化

关于深度可分离卷积的理解

DW卷积、PW卷积、转置卷积、膨胀卷积（空洞卷积）、可变形卷积一次看个够

转置卷积（Transposed Convolution）