✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步精进,matlab项目合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信条:格物致知。
更多Matlab仿真内容点击👇
智能优化算法 神经网络预测 雷达通信 无线传感器
信号处理 图像处理 路径规划 元胞自动机 无人机 电力系统
⛄ 内容介绍
机器人技术是20世纪自动控制领域最辉煌的成就。移动机器人也得到了世界各国政府的重视,成为了最具发展潜力和发展前景的应用型产业。为推动和促进机器人和自动化技术的飞速发展,各国产、学、研相关机构均投入大量资源进行机器人技术开发。机器人竞赛是综合性技术的较量,其激烈对抗的精彩过程吸引了不少大学生爱好者,已经成为培养创新人才和发展机器人技术的重要平台。 本文以中国机器人大赛为研究背景,对移动机器人路径规划问题做了详细描述,简单介绍了几种常用的路径规划算法,并总结了其优劣性。“机器人游中国”竞赛项目的制胜之道就是在规定的时间内游历更多的景点,获取更多的分数。针对研究对象和竞赛规则,建立了比赛得分的数学模型,提出了最合算景点的概念及其数学模型,从而设计了一种适合“机器人游中国”竞赛项目参赛机器人路径规划的启发式算法。算法的思路简单清晰,计算速度快,并且实验表明该算法在比赛中能获得良好的比赛成绩。 遗传算法也是常用的路径规划算法之一。
⛄ 部分代码
%Generate 1st population
function popparent = InitPop(Popsize,RPNUM,adjacency,Mixrate)
popparent = zeros(Popsize,RPNUM);
for i = 1:Popsize
%if(i<=(Mixrate*Popsize))
%Normal 1st gen
%popparent(i,:)=randperm(RPNUM); %1:RPNUM integers without repetition
%else
%Elite 1st gen
popparent(i,:) = Nearest(RPNUM,adjacency); %Use Nearest Neighbor to get Elite 1st gen
%end
end
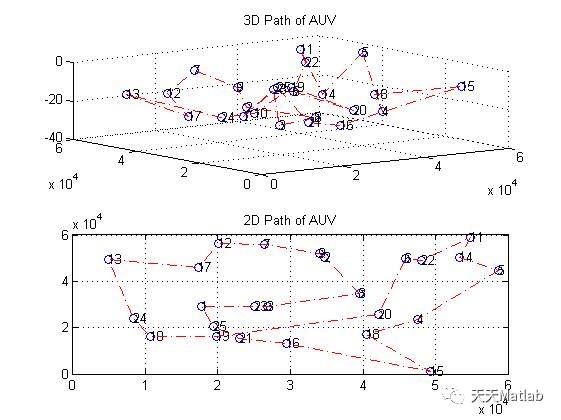
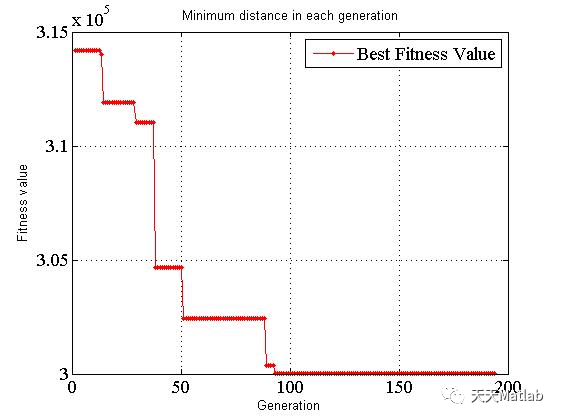
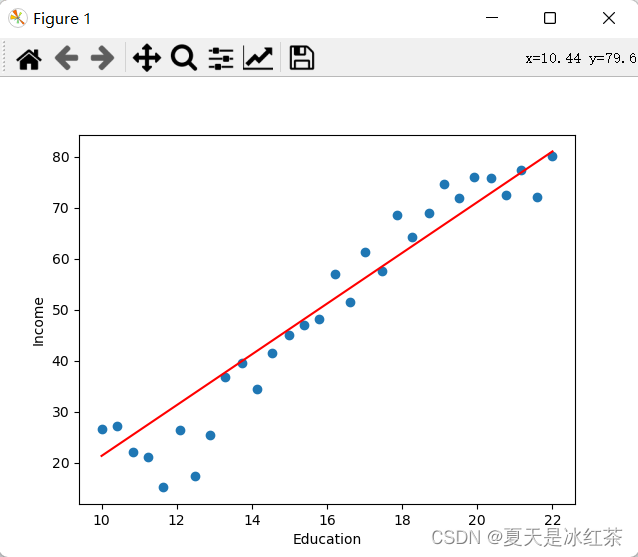
⛄ 运行结果
⛄ 参考文献
[1]李晓明. 基于遗传算法的多源多目路径规划问题研究[D]. 山东科技大学, 2014.
⛄ Matlab代码关注
❤️部分理论引用网络文献,若有侵权联系博主删除
❤️ 关注我领取海量matlab电子书和数学建模资料

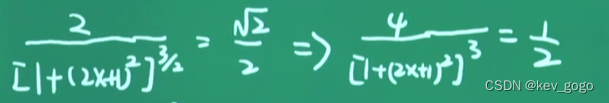



![[前端框架]-VUE(上篇)](https://img-blog.csdnimg.cn/b6a4e0ff37834237b2b3372ec0479cd2.png)