一、基础复习
- 函数的基本用法 创建和调用函数 函数的形参与实参等等
- 函数的几种参数 位置参数、关键字参数、默认参数等
- 函数的收集参数*args **args 解包参数详解
- 函数中参数的作用域 局部作用域 全局作用域 global语句 嵌套函数 nonlocal语句等详解
- 函数的闭包(工厂函数)
- lambda()函数表达式、map()、filter()函数详解
- 生成器的定义、使用和产生生成器的两种方法详解
- 函数的递归、递归和迭代的区别详解
二、汉诺塔
1.汉诺塔简介
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
 汉诺塔移动规则:
汉诺塔移动规则:
- 规则一:一次只能移动一枚金片。
- 小片必须在大片的上面。
2.汉诺塔代码编写
汉诺塔的代码编写,主要用到了函数的递归, 对递归不熟悉的可以看一下函数的递归、递归和迭代的区别详解
例1:当汉诺塔层数为5时
def hanoi(n,x,y,z):
if n==1:
print(x,'-->',z) # 如果只有1层,直接将金片从x移动到z
else:
hanoi(n-1,x,z,y) # 将x上的n-1个金片移动到y
print(x,'-->',z) # 将最底下的金片从x移动到z
hanoi(n-1,y,x,z) # 将y上的n-1个金片移动到z
n=int(input('请输入汉诺塔的层数:'))
hanoi(n,'A','B','C')
结果:
>>>
================= RESTART: E:\xiaojiayu code\049讲:函数(IX).py =================
请输入汉诺塔的层数:5
A --> C
A --> C
B --> C
A --> C
B --> C
B --> C
A --> C
A --> C
B --> C
B --> C
A --> C
B --> C
A --> C
A --> C
B --> C
A --> C
B --> C
B --> C
A --> C
B --> C
A --> C
A --> C
B --> C
B --> C
A --> C
A --> C
B --> C
A --> C
B --> C
B --> C
A --> C
例2:当汉诺塔层数为3时
结果:
>>>
================= RESTART: E:\xiaojiayu code\049讲:函数(IX).py =================
请输入汉诺塔的层数:3
A --> C
A --> C
B --> C
A --> C
B --> C
B --> C
A --> C
>>>
汉诺塔n为3时,代码解释如下:
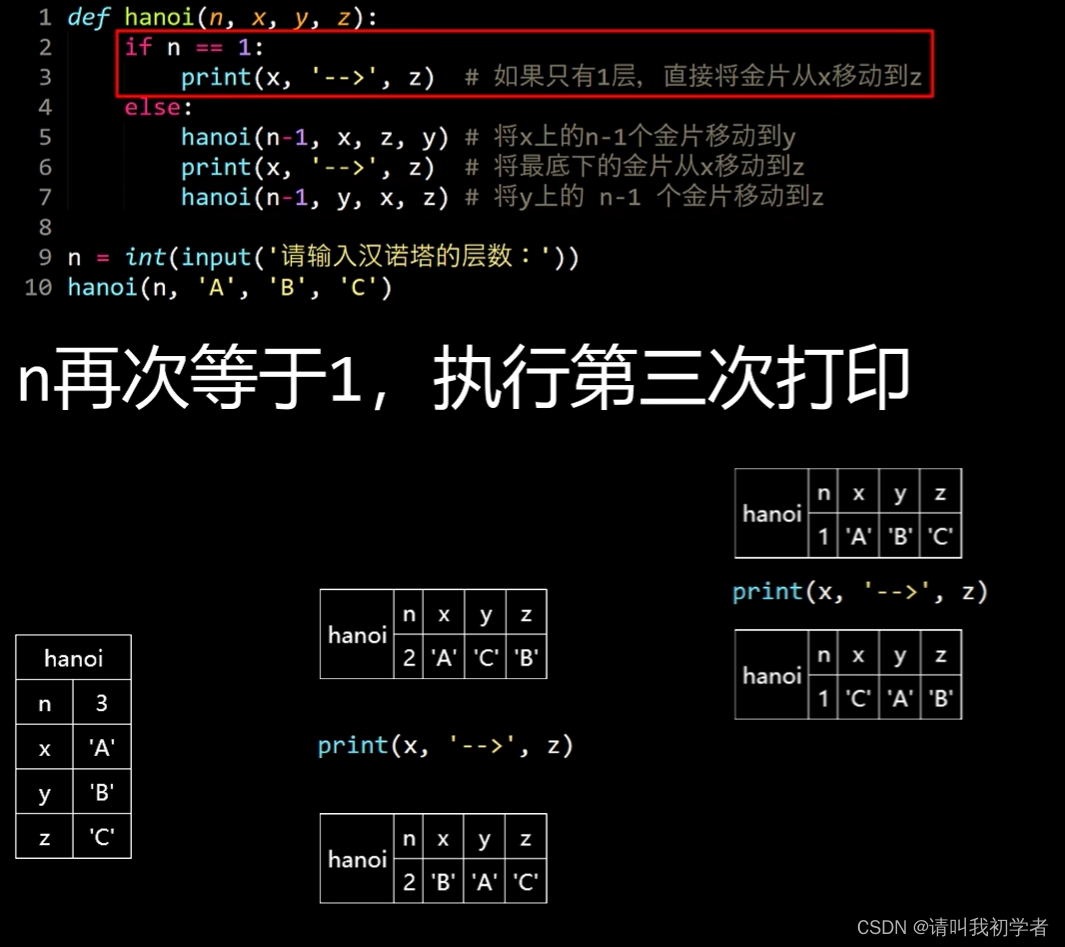
课后题:
1.给定一个整数 n,请编写一个递归函数,计算从 1 + 2 + 3 + … + n 的结果(比如 n = 10,那么结果就是 55)。
代码:
>>> def get_sum(n):
... if n == 1:
... return 1
... else:
... return n + get_sum(n-1)
...
>>> get_sum(10)
55
>>> get_sum(100)
5050
解析:如果是 n 等于 1 就返回 1(结束递归),否则就是返回 n + get_sum(n-1),递归其实很好理解的对吧~
2.给定一个整数 n,请编写一个递归函数,判断该整数是否为 2 的幂次方。如果是返回 True,否则返回 False。
代码:
>>> def isPowerOfTwo(n):
... if n > 0:
... if n == 1:
... return True
... if n % 2 == 1:
... return False
... return isPowerOfTwo(n/2)
... else:
... return False
...
>>> isPowerOfTwo(1)
True
>>> isPowerOfTwo(0)
False
>>> isPowerOfTwo(8)
True
解析:if n % 2 == 1 这句虽然不要也可以,但是有它可以极大地提高代码的工作效率。
3.请实现一个递归函数,要求只使用加号运算符(+)来实现乘法运算的结果。
我的代码:
>>> def mul(x,y):
if x<1:
return 0
else:
return y+mul(x-1,y)
# 结果
>>> mul(3,4)
12
>>> mul(3,5)
15
>>> mul(12,24)
288
答案代码:
>>> def mul(x, y):
... if x == 0 or y == 0:
... return 0
... if x == 1:
... return y
... if y == 1:
... return x
... if x < y:
... return mul(x-1, y) + y
... else:
... return mul(x, y-1) + x
# 结果
>>> mul(3, 4)
12
>>> mul(3, 5)
15
>>> mul(12, 24)
288
4.给定一个列表 L,请编写一个递归函数,找到该列表中最大的元素。
代码:
>>> def get_max(L):
... if len(L) == 2:
... return L[0] if L[0] > L[1] else L[1]
... else:
... sub = get_max(L[1:])
... return L[0] if L[0] > sub else sub
解析:如果长度为 2,直接比较列表仅剩的两个元素大小;否则通过 get_max(L[1:]) 每次递归减少 1 个元素(sub 表示从剩余的部分拿出最大的数)。
5.假设僧侣每秒钟都能正确地移动一枚金片,请问将 64 枚金片从一根银针移动到另外一根银针上,大概需要使用多少时间?
解析:可能你会想着拿课堂中汉诺塔的代码进行修改,然后试图让程序移动完再顺便告诉你总共移动了多少次,像下面这样:
i = 0
def hanoi(n, x, y, z):
global i
if n == 1:
i += 1
else:
hanoi(n-1, x, z, y)
i += 1
hanoi(n-1, y, x, z)
n = int(input('请输入汉诺塔的层数:'))
hanoi(n, 'A', 'B', 'C')
print(i)
但问题是如果输入的层数是 64 的话,代码执行的时间会相当相当久,以致于你可能等不到结果。
让我们先来看看汉诺塔的实现代码:
def hanoi(n, x, y, z):
if n == 1:
print(x, '-->', z) # 如果只有 1 层,直接将金片从 x 移动到 z
else:
hanoi(n-1, x, z, y) # 将 x 上的 n-1 个金片移动到 y
print(x, '-->', z) # 将最底下的金片从 x 移动到 z
hanoi(n-1, y, x, z) # 将 y 上的 n-1 个金片移动到 z
n = int(input('请输入汉诺塔的层数:'))
hanoi(n, 'A', 'B', 'C')
递归调用和移动金片的规律是这样的:
g(n) = g(n-1) + 1 + g(n-1)
也就是:
g(n) = 2 * g(n-1) + 1
当 n == 1 的时候,g(1) == 1
那么我们就可以根据这条规律,写出如下代码:
>>> def g(n):
... if n == 1:
... return 1
... else:
... return 2 * g(n-1) + 1
>>> g(64)
18446744073709551615
>>> g(64) / 365 / 24 / 3600
584942417355.072
题目来自小甲鱼python函数(IX)