Lasso回归的模型可以写作

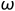与一般线性回归相比, Lasso回归加入了回归项系数的一范数, 这样做是为了防止线性回归过程发生的过拟合现象. 直观点看, 其将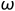的分量限制在了一个以圆点为中心以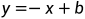为边的正方形内. 与岭回归相比, 该模型得到的系数矩阵更为稀疏.

由于函数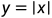在0点不可导, 因而Lasso回归无法通过简单的求梯度求解其结果. 本文仅整理了坐标下降法对该模型的求解过程. 也就是对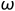的每个分量采取梯度下降的方式, 使得其对每个分量的分量趋近于0. 首先将Lasso回归的模型重写成分量形式:

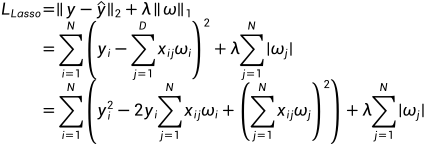
对分量求偏导可得

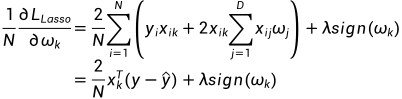
这里对于取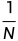我的理解是在对每个分量求偏导, 暂时没找到令我信服的解释. 因而有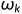的表达式为

其中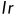表示学习率.

由此, 可得其代码(此代码只是为了更好的了解其求解过程)

import copy
import numpy as np
# 自动生成求解数据
from sklearn.datasets import make_regression


def lasso_recurrence(x_train, y_train, lam, lr, epochs):
    xmat = np.mat(x_train)
    ymat = np.mat(y_train).T
    n, m = x_train.shape
    omega = np.ones([m, 1])
    # 外层迭代迭代总搜索次数
    for i in range(epochs):
        # preomega表示上次搜索的omega
        pre_omega = copy.copy(omega)
        for j in range(m):
            # 内层迭代迭代每个维度j的搜索次数
            for k in range(epochs):
                yhat = xmat * omega
                temp = xmat[:, j].T * (yhat - ymat) / n + lam * np.sign(omega[j])
                omega[j] = omega[j] - temp * lr
                # 若该omega的第j个维度已经足够接近0则终止内层迭代
                if np.abs(omega[j]) < 1e-3:
                    break
        # 若两次迭代的omega的差别小于1e-3则终止外层迭代
        diffomega = np.array(list(map(lambda x: abs(x) < 1e-3, pre_omega - omega)))
        if diffomega.all() < 1e-3:
            break
    return omega


if __name__ == '__main__':
    X, y = make_regression(200, 5, noise=1)
    print(lasso_recurrence(X, y, 0.1, 0.5, 1000))

同样的可以通过调用sklearn.liner_model中的Lasso对其进行实现, 具体代码如下

from sklearn.datasets import make_regression
from sklearn.linear_model import Lasso


if __name__ == '__main__':
    X, y = make_regression(200, 5, noise=1)
    model = Lasso(alpha=0.1, max_iter=1000)
    model.fit(X, y)
    print(model.coef_)

比较两个方式的结果有

维度较高的情况下可能差异较大, 当数据维度降低时有

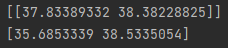
如此完成对Lasso回归的整理. 本文参考b站Lasso回归的讲解

回归分析-Lasso回归