1、最大间距(数组,桶排序)
给定一个无序的数组,找出数组在排序之后,相邻元素之间最大的差值。
如果数组元素个数小于 2,则返回 0。
示例 1:
输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。
示例 2:
输入: [10]
输出: 0
解释: 数组元素个数小于 2,因此返回 0。
说明:
- 你可以假设数组中所有元素都是非负整数,且数值在 32 位有符号整数范围内。
- 请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。
选项代码:
class Solution(object):
def maximumGap(self, nums):
if len(nums) < 2:
return 0
min_val, max_val = min(nums), max(nums)
if min_val == max_val:
return 0
n = len(nums) + 1
step = (max_val - min_val) // n
exist = [0 for _ in range(n + 1)]
max_num = [0 for _ in range(n + 1)]
min_num = [0 for _ in range(n + 1)]
for num in nums:
idx = self.findBucketIndex(num, min_val, max_val, n)
max_num[idx] = num if not exist[idx] else max(num, max_num[idx])
min_num[idx] = num if not exist[idx] else min(num, min_num[idx])
exist[idx] = 1
res = 0
pre = max_num[0]
for i in range(1, n + 1):
if exist[i]:
res = max(res, min_num[i] - pre)
pre = max_num[i]
return res
def findBucketIndex(self, num, min_val, max_val, n):
return int((num - min_val) * n / (max_val - min_val))
if __name__ == "__main__":
sol = Solution()
nums = [3,6,9,1]
answer=sol.maximumGap(nums)
print(answer)2、将有序数组转换为二叉搜索树(树,二叉搜索树)
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:
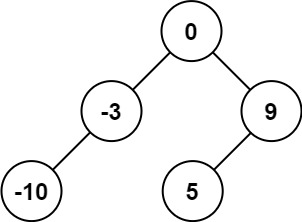
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

示例 2:
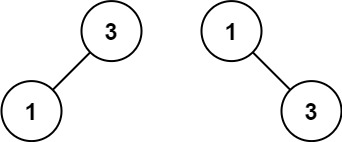
输入:nums = [1,3]
输出:[3,1]
解释:[1,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 按 严格递增 顺序排列
选项代码:
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class Solution:
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if not nums:
return None
mid = len(nums) // 2
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[:mid])
root.right = self.sortedArrayToBST(nums[mid + 1:])
return root
if __name__ == "__main__":
sol = Solution()
nums = [-10,-3,0,5,9]
answer=sol.sortedArrayToBST(nums)
print(answer)3、跳跃游戏 II(贪心、数组)
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
选项代码:
class Solution:
def jump(self, nums):
if len(nums) <= 1:
return 0
end = 0 + nums[0]
start = 0
step = 1
maxDis = 0 + nums[0]
while end < len(nums) - 1:
for i in range(start + 1, end + 1):
maxDis = max(maxDis, nums[i] + i)
start = end
end = maxDis
step += 1
return step
# %%
s = Solution()
print(s.jump(nums = [2,3,0,1,4]))