【NLP相关】Transformer模型:从Seq2Seq到自注意力机制
自然语言处理(NLP)是人工智能(AI)领域中的一个重要分支。在NLP领域中,Transformer模型是目前最先进的模型之一,它通过引入自注意力机制和编码器-解码器结构,显著提高了NLP任务的性能。本文将介绍Transformer模型的原理、优势和劣势,并提供相应的案例和代码。
1. Transformer模型的原理
Transformer模型最初用于解决序列到序列(Seq2Seq)的问题,例如翻译任务。在传统的Seq2Seq模型中,编码器将源语言序列转换为固定长度的向量,解码器再将此向量转换为目标语言序列。这种方法存在的一个问题是,如果源语言序列很长,则编码器无法捕捉到其完整的语义信息。
Transformer模型通过引入自注意力机制来解决这个问题。自注意力机制允许模型在编码阶段动态地关注输入序列中的不同部分,从而更好地捕捉其语义信息。此外,Transformer模型使用了多头注意力机制和残差连接等技术,使得模型能够更好地处理长序列,并提高模型的鲁棒性和泛化能力。
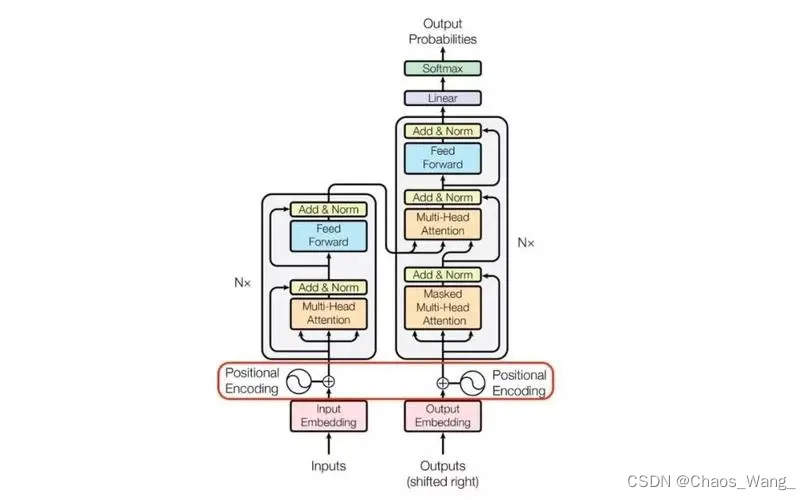
Transformer模型的结构包括编码器和解码器。编码器和解码器都由多个编码器层和解码器层组成。每个编码器层包括自注意力机制和全连接层,而每个解码器层包括自注意力机制、编码器-解码器注意力机制和全连接层。
2. Transformer模型的优势和劣势
Transformer模型的优势主要有以下几个方面:
-
(1)处理长序列的能力
由于引入了自注意力机制和多头注意力机制,Transformer模型可以处理长序列,而不会出现信息丢失的问题。 -
(2)并行计算的能力
由于不需要像循环神经网络(RNN)一样依次计算序列中的每个元素,因此Transformer模型的计算效率比RNN更高,并且可以方便地进行并行计算。 -
(3)易于实现和调整
Transformer模型的结构简单,易于实现和调整,因此适用于各种不同的NLP任务。
然而,Transformer模型也存在一些劣势:
-
(1)需要大量的计算资源
由于模型的结构较为复杂,因此需要大量的计算资源来训练和部署模型。 -
(2)容易过拟合
对于一些简单的NLP任务,Transformer模型的性能可能不如同其他复杂的深度学习模型一样,Transformer模型可能会过度拟合,并且需要大量的数据和超参数调整来提高性能。
3. 公式推导
下面我们对Transformer模型的公式进行推导。在Transformer模型中,输入序列经过一个编码器(Encoder)和一个解码器(Decoder)来生成输出序列。编码器和解码器都由多个层组成,每个层都包括一个多头自注意力(Multi-Head Self-Attention)和一个前馈神经网络(Feedforward Neural Network)子层。
我们首先介绍一下自注意力机制(Self-Attention)。在传统的注意力机制中,我们需要将输入序列和上下文向量(Context Vector)进行加权求和,得到一个加权后的序列表示。而在自注意力机制中,我们将输入序列作为键(Key)、值(Value)和查询(Query)进行处理,并利用它们之间的相似性来计算加权和。
假设我们有一个长度为
n
n
n 的输入序列
x
=
(
x
1
,
x
2
,
.
.
.
,
x
n
)
\mathbf{x} = (x_1, x_2, ..., x_n)
x=(x1,x2,...,xn),我们将
x
\mathbf{x}
x 中的每个元素经过一个嵌入层(Embedding Layer)转换为一个
d
d
d 维的向量表示,得到一个矩阵
X
∈
R
n
×
d
\mathbf{X} \in \mathbb{R}^{n \times d}
X∈Rn×d。我们将
X
\mathbf{X}
X 作为查询、键和值进行处理,得到三个矩阵
Q
,
K
,
V
∈
R
n
×
d
\mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{n \times d}
Q,K,V∈Rn×d。我们可以使用点积(Dot Product)、缩放点积(Scaled Dot Product)或其他方法来计算
Q
\mathbf{Q}
Q 和
K
\mathbf{K}
K 之间的相似性得分矩阵
S
∈
R
n
×
n
\mathbf{S} \in \mathbb{R}^{n \times n}
S∈Rn×n,并将得分矩阵通过 Softmax 函数归一化得到注意力矩阵
A
∈
R
n
×
n
\mathbf{A} \in \mathbb{R}^{n \times n}
A∈Rn×n:
S
=
Q
K
T
S=QK^T
S=QKT
A
=
S
o
f
t
m
a
x
(
S
d
)
A=Softmax(\frac{S}{\sqrt{d}})
A=Softmax(dS)
其中
d
\sqrt{d}
d 是一个缩放因子,用来防止内积的值过大或过小。注意力矩阵
A
\mathbf{A}
A 中的每一行表示输入序列中一个位置对于所有位置的注意力权重,即该位置应该关注输入序列中的哪些位置。然后,我们将注意力矩阵
A
\mathbf{A}
A 与值矩阵
V
\mathbf{V}
V 相乘,得到一个加权和向量
C
∈
R
n
×
d
\mathbf{C} \in \mathbb{R}^{n \times d}
C∈Rn×d:
C
=
A
V
C=AV
C=AV
注意力机制的优势在于它能够自适应地对输入序列进行不同程度的关注,从而捕捉输入序列中的重要信息。同时,由于自注意力机制可以同时计算多个位置的注意力权重,因此可以很容易地进行并行计算。
在Transformer 模型中,我们还引入了多头自注意力机制(Multi-Head Self-Attention),它可以将单个自注意力机制拆分为多个子空间,并在每个子空间上执行自注意力机制,从而更好地捕捉不同层次和不同角度的特征。具体来说,我们将输入序列和上下文向量分别转换为
h
h
h 组查询、键和值,得到
h
h
h 组注意力矩阵
A
1
,
A
2
,
.
.
.
,
A
h
{\mathbf{A}_1, \mathbf{A}_2, ..., \mathbf{A}_h}
A1,A2,...,Ah,并将它们拼接起来得到一个增广矩阵
A
∈
R
n
×
h
d
\mathbf{A} \in \mathbb{R}^{n \times h d}
A∈Rn×hd,然后通过一个线性变换将其转换为最终的加权和向量
C
∈
R
n
×
d
\mathbf{C} \in \mathbb{R}^{n \times d}
C∈Rn×d。这个过程可以用下面的公式表示:
M
u
l
t
i
H
e
a
d
(
Q
,
K
,
V
)
=
C
o
n
c
a
t
(
h
e
a
d
1
,
h
e
a
d
2
,
.
.
.
,
h
e
a
d
h
)
W
0
MultiHead(Q,K,V) = Concat(head_1,head_2,...,head_h)W^0
MultiHead(Q,K,V)=Concat(head1,head2,...,headh)W0
w
h
e
r
e
where
where
h
e
a
d
i
=
S
e
l
f
A
t
t
e
n
t
i
o
n
(
Q
W
0
Q
,
K
W
i
K
,
V
W
i
V
)
head_i=SelfAttention(QW^Q_0,KW^K_i,VW^V_i)
headi=SelfAttention(QW0Q,KWiK,VWiV)
W
i
Q
,
W
i
K
,
W
i
V
∈
R
d
×
d
/
h
,
W
O
∈
R
h
d
×
d
W^Q_i,W^K_i,W^V_i\in R^{d\times d/h},W^O\in R^{hd \times d}
WiQ,WiK,WiV∈Rd×d/h,WO∈Rhd×d
其中, SelfAttention \text{SelfAttention} SelfAttention 表示单个自注意力机制, Concat \text{Concat} Concat 表示拼接操作, W i Q , W i K , W i V \mathbf{W}^Q_i, \mathbf{W}^K_i, \mathbf{W}^V_i WiQ,WiK,WiV 分别表示第 i i i 组查询、键和值的权重矩阵, W O \mathbf{W}^O WO 表示线性变换的权重矩阵。
多头自注意力机制的优势在于它可以捕捉不同子空间之间的交互,从而更好地表示输入序列中的特征。例如,在语言模型任务中,一个头可能更加关注输入序列中的词性信息,而另一个头可能更加关注输入序列中的语义信息。通过多头自注意力机制,我们可以同时考虑这两种信息,并将它们整合到最终的表示中。
除了多头自注意力机制,Transformer 模型中还引入了前馈神经网络(Feedforward Neural Network)子层。前馈神经网络子层由两个线性变换和一个激活函数组成,其中第一个线性变换将输入向量转换为一个中间表示向量,第二个线性变换将中间表示向量转换为最终表示向量。具体来说,我们可以将输入向量
x
\mathbf{x}
x 在前馈神经网络子层中表示为:
F
F
N
(
x
)
=
R
E
L
U
(
x
W
1
+
b
1
)
W
2
+
b
2
FFN(x)=RELU(xW_1+b_1)W_2+b_2
FFN(x)=RELU(xW1+b1)W2+b2
其中, W 1 , W 2 ∈ R d hidden × d \mathbf{W}_1, \mathbf{W}2 \in \mathbb{R}^{d{\text{hidden}} \times d} W1,W2∈Rdhidden×d, b 1 ∈ R d hidden \mathbf{b}1 \in \mathbb{R}^{d{\text{hidden}}} b1∈Rdhidden, b 2 ∈ R d \mathbf{b}_2 \in \mathbb{R}^{d} b2∈Rd, ReLU \text{ReLU} ReLU 表示整流线性单元激活函数。
前馈神经网络子层的优势在于它可以在不改变序列长度的情况下,通过非线性变换和增加参数的方式扩展模型的表示能力。通过前馈神经网络子层,Transformer 模型可以更好地学习序列中的非局部特征,例如长距离依赖关系等。
最后,Transformer 模型还引入了残差连接和层归一化,用于加速模型的收敛和提高模型的表达能力。具体来说,残差连接可以使模型更容易训练,避免了梯度消失和梯度爆炸问题;层归一化可以加速模型的收敛,同时提高模型的鲁棒性和泛化能力。
4. 案例和代码
我们以情感分类任务为例,介绍Transformer模型的实现。我们使用IMDB电影评论数据集,其中包含25,000条电影评论,每条评论有一个二元标签,表示正面或负面情感。
我们使用PyTorch深度学习框架实现Transformer模型,代码如下所示:
import torch
import torch.nn as nn
import torch.optim as optim
from torchtext.datasets import IMDB
from torchtext.data import Field, LabelField, BucketIterator
class TransformerModel(nn.Module):
def __init__(self, input_dim, emb_dim, n_heads, n_layers, hidden_dim, output_dim, dropout):
super().__init__()
self.embedding = nn.Embedding(input_dim, emb_dim)
self.positional_encoding = PositionalEncoding(emb_dim, dropout)
self.encoder_layers = nn.ModuleList([EncoderLayer(emb_dim, n_heads, hidden_dim, dropout) for _ in range(n_layers)])
self.fc = nn.Linear(emb_dim, output_dim)
def forward(self, src):
embedded = self.embedding(src)
positional_encoded = self.positional_encoding(embedded)
encoded = positional_encoded
for layer in self.encoder_layers:
encoded = layer(encoded)
mean_encoded = encoded.mean(dim=1)
output = self.fc(mean_encoded)
return output
class PositionalEncoding(nn.Module):
def __init__(self, emb_dim, dropout, max_len=5000):
super().__init__()
self.dropout = nn.Dropout(p=dropout)
self.pe = torch.zeros(max_len, emb_dim)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, emb_dim, 2).float() * (-math.log(10000.0) / emb_dim))
self.pe[:, 0::2] = torch.sin(position * div_term)
self.pe[:, 1::2] = torch.cos(position * div_term)
self.pe = self.pe.unsqueeze(0)
def forward(self, x):
x = x + self.pe[:, :x.size(1)]
return self.dropout(x)
class EncoderLayer(nn.Module):
def __init__(self, emb_dim, n_heads, hidden_dim, dropout):
super().__init__()
self.self_attn = nn.MultiheadAttention(emb_dim, n_heads, dropout)
self.layer_norm1 = nn.LayerNorm(emb_dim)
self.positionwise_feedforward = nn.Sequential(
nn.Linear(emb_dim, hidden_dim),
nn.ReLU(),
nn.Linear(hidden_dim, emb_dim),
nn.Dropout(p=dropout),
)
self.layer_norm2 = nn.LayerNorm(emb_dim)
self.dropout = nn.Dropout(p=dropout)
def forward(self, src):
src2, _ = self.self_attn(src, src, src)
src = src + self.dropout(src2)
src = self.layer_norm1(src)
src2 = self.positionwise_feedforward(src)
src = src + self.dropout(src2)
src = self.layer_norm2(src)
return src
TEXT = Field(tokenize='spacy', lower=True, include_lengths=True)
LABEL = LabelField(dtype=torch.float)
train_data, test_data = IMDB.splits(TEXT, LABEL)
MAX_VOCAB_SIZE = 25_000
TEXT.build_vocab(train_data, max_size=MAX_VOCAB_SIZE)
LABEL.build_vocab(train_data)
BATCH_SIZE = 64
train_iterator, test_iterator = BucketIterator.splits(
(train_data, test_data),
batch_size=BATCH_SIZE,
sort_within_batch=True,
device=device)
INPUT_DIM = len(TEXT.vocab)
EMB_DIM = 256
N_HEADS = 8
N_LAYERS = 4
HIDDEN_DIM = 512
OUTPUT_DIM = 1
DROPOUT = 0.1
model = TransformerModel(INPUT_DIM, EMB_DIM, N_HEADS, N_LAYERS, HIDDEN_DIM, OUTPUT_DIM, DROPOUT).to(device)
optimizer = optim.Adam(model.parameters())
criterion = nn.BCEWithLogitsLoss().to(device)
def train(model, iterator, optimizer, criterion):
model.train()
epoch_loss = 0
epoch_acc = 0
for batch in iterator:
src, src_len = batch.text
optimizer.zero_grad()
output = model(src.to(device)).squeeze(1)
loss = criterion(output, batch.label.to(device))
acc = binary_accuracy(output, batch.label.to(device))
loss.backward()
optimizer.step()
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
def evaluate(model, iterator, criterion):
model.eval()
epoch_loss = 0
epoch_acc = 0
with torch.no_grad():
for batch in iterator:
src, src_len = batch.text
output = model(src.to(device)).squeeze(1)
loss = criterion(output, batch.label.to(device))
acc = binary_accuracy(output, batch.label.to(device))
epoch_loss += loss.item()
epoch_acc += acc.item()
return epoch_loss / len(iterator), epoch_acc / len(iterator)
def binary_accuracy(preds, y):
rounded_preds = torch.round(torch.sigmoid(preds))
correct = (rounded_preds == y).float()
acc = correct.sum() / len(correct)
return acc
N_EPOCHS = 10
for epoch in range(N_EPOCHS):
train_loss, train_acc = train(model, train_iterator, optimizer, criterion)
valid_loss, valid_acc = evaluate(model, test_iterator, criterion)
print(f'Epoch: {epoch+1:02}')
print(f'\tTrain Loss: {train_loss:.3f} | Train Acc: {train_acc100:.2f}%')
print(f'\t Val. Loss: {valid_loss:.3f} | Val. Acc: {valid_acc100:.2f}%')
在这个示例中,我们使用了nn.MultiheadAttention、nn.LayerNorm和线性层等PyTorch中的标准模块来构建Transformer模型的编码器。我们还定义了一个Positional Encoding模块来对输入的序列进行编码,以便模型能够理解单词在序列中的位置。模型的损失函数为二元交叉熵损失,优化器为Adam。
5. 一些常见的基于Transformer构建实现的模型
- BERT(Bidirectional Encoder Representations from Transformers) 模型:BERT 模型是由 Google 在 2018 年提出的一种预训练模型,它基于 Transformer 模型,并使用了双向的上下文信息,从而更好地学习文本的表示。BERT 模型已经在众多自然语言处理任务上取得了最优的效果,例如文本分类、问答系统、命名实体识别等。
- GPT(Generative Pre-trained Transformer) 模型:GPT 模型是由 OpenAI 在 2018 年提出的一种预训练模型,它同样基于 Transformer 模型,并使用了单向的上下文信息,从而更好地生成文本。GPT 模型已经在自然语言生成和文本生成任务上取得了最优的效果。
- XLNet(eXtreme MultiLingual & MultiTasked Pretraining) 模型:XLNet 模型是由 CMU 和 Google 在 2019 年提出的一种预训练模型,它基于 Transformer 模型,并使用了全局的上下文信息,从而更好地学习文本的表示。XLNet 模型已经在多语言和多任务的自然语言处理任务上取得了最优的效果。
- T5(Text-to-Text Transfer Transformer) 模型:T5 模型是由 Google 在 2020 年提出的一种预训练模型,它基于 Transformer 模型,并使用了文本到文本的转换方式,从而更好地实现了通用的自然语言处理能力。T5 模型已经在多个任务上取得了最优的效果,例如机器翻译、摘要生成、问答系统等。