变分自编码器是自编码器的改进版本，自编码器AE是一种无监督学习，但它无法产生新的内容，变分自编码器对其潜在空间进行拓展，使其满足正态分布，情况就大不一样了。

自编码器AE，auto-encoder

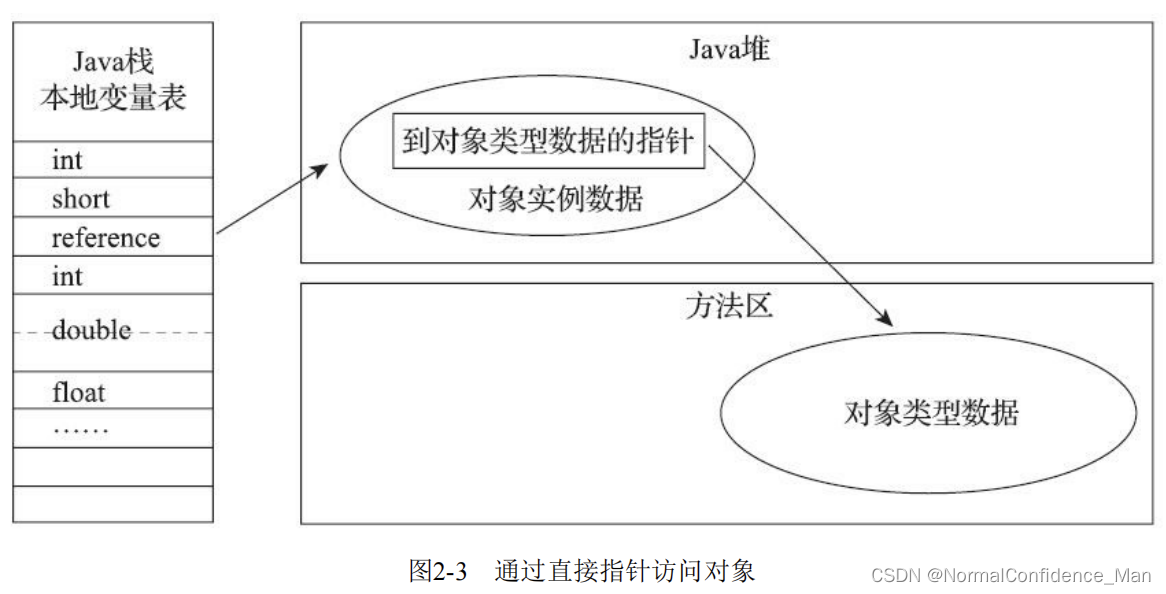
自编码器是通过对输入X进行编码后得到一个低维的向量z，然后根据这个向量还原出输入X。通过对比X与$\stackrel{\sim }{X}$的误差，再利用神经网络去训练使得误差逐渐减小，从而达到非监督学习的目的。
下图为AE的架构图:

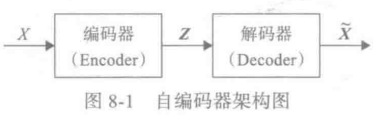
自编码器不能随意产生合理的潜在变量，从而导致它无法产生新的内容。因为潜在变量Z都是编码器从原始图片中产生的。为了解决这一问题，研究人员对潜在空间Z(潜在变量对应的空间) 增加一些约束，使 Z 满足正态分布，由此就出现了VAE模型， VAE对编码器添加约束，就是强迫它产生服从单位正态分布的潜在变量。正是这种约束，把VAE和 AE 区分开来。

VAE

变分自编码器关键一点就是增加一个对潜在空间Z的正态分布约束，如何确定这个正态分布就成为主要目标，我们知道要确定正态分布，只要确定其两个参数: 均值$\mu$和标准差$\sigma$。那如何确定 $\mu ,\sigma$呢？用一般的方法或估计比较麻烦效果也不好，研究人员发现**用神经网络去拟合，简单效果也不错。**下图为VAE的架构图：

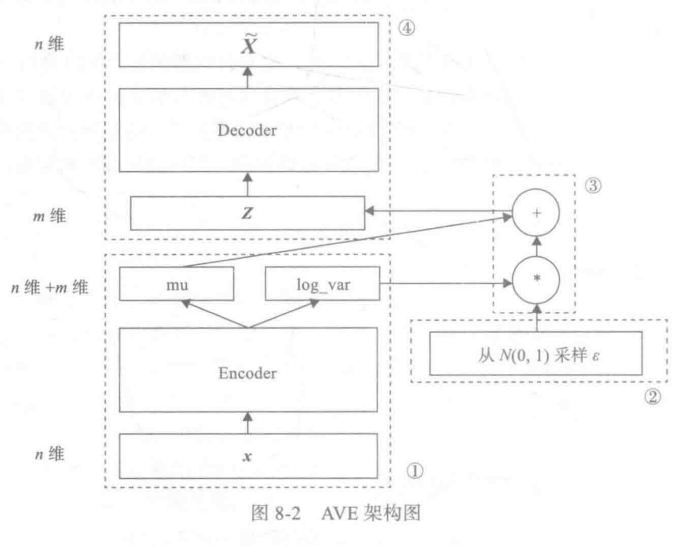
上图中，模块①的功能把输入样本X通过编码器输出两个m维向量($\mu ,log\_var$), 这两个向量是潜在空间(假设满足正态分布)的两个参数(相当于均值和方差)。那么如何从这个潜在空间采样一个点 Z ?

这里假设潜在正态分布能生成输入图像，从标准正态分布 N(0, 1)中采样一个 $ϵ$(模块②的功能)， 然后使
$$Z=\mu +e^{log\_var}\ast ϵ$$
这也是模块③的主要功能。
Z是从潜在空间抽取的一个向量，Z通过解码器生成一个样本$\stackrel{\sim }{X}$, 这是模块④的功能。这里的 $ϵ$ 是随机采样的，这就可以保证潜在空间的连续性，良好的结构性。而这些特性使得潜在空间的每个方向都表示数据中有意义的变化方向。

以上的这些步骤构成整个网络的前向传播过程，那反向传播应如何进行？要确定反向传播就会设计损失函数，损失函数是衡量模型优劣的主要指标。这里我们需要从以下两个方面进行衡量。
1)生成的新图像与原图像的相似度;
2)隐含空间的分布与正态分布的相似度。

度量图像的相似度一般采用交叉熵(如nn.BCELoss) , 度量两个分布的相似度一般采用KL散度(Kullback-Leibler divergence)。这两个度量的和构成了整个模型的损失函数。

以下是损失函数的具体代码，VAE损失函数的推导过程可以参考原论文

# 定义重构损失函数及KL散度
reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
kl_div = -0.5*torch.sum(1+log_var-mu.pow(2)-log_var.exp())
# 两者相加得总损失
loss = reconst_loss + kl_div

讲讲为什么是log_var

这里可以看成 log_var = $\log \sigma$，所以$Z=\mu +e^{log\_var}\ast ϵ$也就是$$Z=\mu +\sigma \ast ϵ$$
其中$ϵ\sim N(0,1)$, 这里涉及到重参数化reparameterization。

为什么要用重参数化技巧

如果想从高斯分布$N(\mu ,{\sigma }^2)$中采样，可以先从标准分布$N(0,1)$采样出 $ϵ$ , 再得到 $Z=\sigma \ast ϵ+\mu$.
这样做的好处是：

1. 如果直接对$N(\mu ,{\sigma }^2)$进行采样得到Z，则Z无法对$\mu ,\sigma$进行求偏导

2. 将随机性转移到了 $ϵ$ 这个常量上，而 $\sigma$和$\mu$则当做仿射变换网络的一部分,这样得到的$Z=\sigma \ast ϵ+\mu$，则Z就可以对$\mu ,\sigma$进行求偏导来计算损失函数，进行求梯度，进行BP。

用VAE生成图像

下面将结合代码，用pytorch实现，为便于说明起见，数据集采用MNIST，整个网络架构如下图所示。

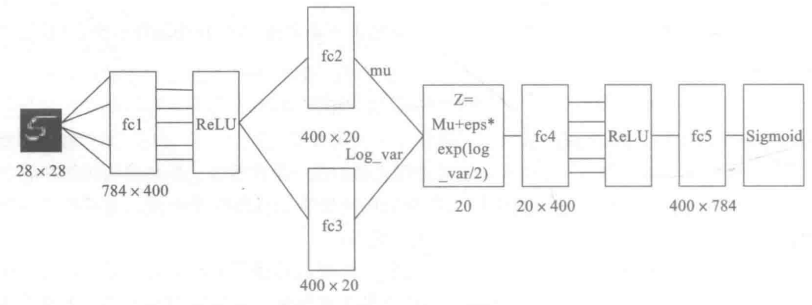
# 1. 导入必要的包
import os 
import torch 
import torch.nn as nn 
import torch.nn.functional as F 
import torchvision 
from torchvision import transforms 
from torchvision.utils import save_image

# 2. 定义一些超参数
image_size = 784 # 28*28 
h_dim = 400 
z_dim = 20 
num_epochs = 30 
batch_size = 128 
learning_rate = 0.001 

# 如果没有文件夹就创建一个文件夹
sample_dir = 'samples'
if not os.path.exists(sample_dir):
    os.makedirs(sample_dir)
                                     

3. 对数据集进行预处理，如转换为Tensor, 把数据集转换为循环，可批量加载的数据集

# 只下载训练数据集即可
# 下载MNIST训练集
dataset = torchvision.datasets.MNIST(root='./data', train=True, 
                                    transform=transforms.ToTensor(),
                                    download=True)

# 数据加载
data_loader = torch.utils.data.DataLoader(dataset=dataset,
                                    batch_size=batch_size,
                                    shuffle=True)

4. 构建VAE模型，主要由Encoder和Decoder两部分组成

# 定义AVE模型
class VAE(nn.Module):
    def __init__(self, image_size=784, h_dim=400, z_dim=20):
        super(VAE, self).__init__()
        self.fc1 = nn.Linear(image_size, h_dim)
        self.fc2 = nn.Linear(h_dim, z_dim)
        self.fc3 = nn.Linear(h_dim, z_dim)
        
        self.fc4 = nn.Linear(z_dim, h_dim)
        self.fc5 = nn.Linear(h_dim, image_size)

    def encoder(self, x):
        h = F.relu(self.fc1(x))
        return self.fc2(h), self.fc3(h)
    
    # 用mu, log_var生成一个潜在空间点z, mu, log_var为两个统计参数，我们假设
    # 这个假设分布能生成图像
    def reparameterize(self, mu, log_var):
        std = torch.exp(log_var/2)
        eps = torch.randn_like(std)
        return mu + eps * std 

    def decoder(self, z):
        h = F.relu(self.fc4(z))
        return F.sigmoid(self.fc5(h))
    
    def forward(self, x):
        mu, log_var = self.encoder(x)
        z = self.reparameterize(mu, log_var)
        x_reconst = self.decoder(z)
        return x_reconst, mu, log_var 
    

5. 选择GPU和优化器

# 选择GPU和优化器
torch.cuda.set_device(1)
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = VAE().to(device)
optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

6. 训练模型，同时保存原图像与随机生成的图像

# 训练模型，同时保存原图像与随机生成的图像
for epoch in range(num_epochs):
    for i, (x, _) in enumerate(data_loader):
        # 获取样本，并前向传播
        x = x.to(device).view(-1, image_size)
        x_reconst, mu, log_var = model(x)

        # 计算重构损失和KL散度(KL散度用于衡量两种分布的相似程度)
        # KL散度的计算可以参考https://shenxiaohai.me/2018/10/20/pytorch-tutorial-advanced-02/
        reconst_loss = F.binary_cross_entropy(x_reconst, x, size_average=False)
        kl_div = -0.5 * torch.sum(1 + log_var - mu.pow(2) - log_var.exp())

        # 反向传播和优化
        loss = reconst_loss + kl_div 
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        if (i+1)%100 == 0:
            print('Epoch [{}/{}], Step [{}/{}], Reconst Loss: {:.4f}, KL Div:{:.4f}'.
                  format(epoch+1, num_epochs, i+1, len(data_loader), reconst_loss.item(), kl_div.item()))

    # 利用训练的模型进行测试
    with torch.no_grad():
        # 保存采样图像，即潜在向量z通过解码器生成的新图像
        # 随机生成的图像
        z = torch.randn(batch_size, z_dim).to(device)
        out = model.decoder(z).view(-1, 1, 28, 28)
        save_image(out, os.path.join(sample_dir, 'sampled-{}.png'.format(epoch+1)))

        # 保存重构图像，即原图像通过解码器生成的图像
        out, _, _ = model(x)
        x_concat = torch.cat([x.view(-1, 1, 28, 28), out.view(-1, 1, 28, 28)], dim=3)
        save_image(x_concat, os.path.join(sample_dir, 'reconst-{}.png'.format(epoch+1)))

7. 展示原图像及重构图像

#显示图片
import matplotlib.pyplot as plt 
import matplotlib.image as mpimg 
import numpy as np 

recons_path = './samples/reconst-30.png'
Image = mpimg.imread(recons_path)
plt.imshow(Image)
plt.axis('off')
plt.show()
# reconst
# 奇数列为原图像，欧数列为原图像重构的图像，可以看出重构效果还不错。

8. 由潜在空间通过解码器生成的新图像，这个图像效果也不错

# sampled
# 为由潜在空间通过解码器生成的新图像，这个图像效果也不错
genPath = './samples/sampled-30.png'
Image = mpimg.imread(genPath)
plt.imshow(Image)
plt.axis('off')
plt.show()

总结：这里构建网络主要用全连接层，有兴趣的读者，可以把卷积层，如果编码层使用卷积层(如nn.Conv2d), 则解码器就需要使用反卷积层(如nn.ConvTranspose2d)。