基于麻雀算法改进的BP神经网络坑基监测，BP神经网络详细原理，

news2024/9/28 13:26:46

目标
背影
BP神经网络的原理
BP神经网络的定义
BP神经网络的基本结构
BP神经网络的神经元
BP神经网络的激活函数，
BP神经网络的传递函数
麻雀算法原理
麻雀算法主要参数
麻雀算法流程图
麻雀算法优化测试函数代码
基于麻雀算法改进的BP神经网络坑基监测
数据
matlab编程实现
效果图
结果分析
展望

背影

坑基监测是很多工程安全的重要能容之一，一旦出现险情，往往来不及处理，需要有一定的提前预判，本文用基于麻雀算法改进的BP神经网络监测基坑，有一定 的提前预判能力，实现监测的智能化。

BP神经网络的原理

BP神经网络的定义

人工神经网络无需事先确定输入输出之间映射关系的数学方程，仅通过自身的训练，学习某种规则，在给定输入值时得到最接近期望输出值的结果。作为一种智能信息处理系统，人工神经网络实现其功能的核心是算法。BP神经网络是一种按误差反向传播(简称误差反传)训练的多层前馈网络，其算法称为BP算法，它的基本思想是梯度下降法，利用梯度搜索技术，以期使网络的实际输出值和期望输出值的误差均方差为最小。

BP神经网络的基本结构

基本BP算法包括信号的前向传播和误差的反向传播两个过程。即计算误差输出时按从输入到输出的方向进行，而调整权值和阈值则从输出到输入的方向进行。正向传播时，输入信号通过隐含层作用于输出节点，经过非线性变换，产生输出信号，若实际输出与期望输出不相符，则转入误差的反向传播过程。误差反传是将输出误差通过隐含层向输入层逐层反传，并将误差分摊给各层所有单元，以从各层获得的误差信号作为调整各单元权值的依据。通过调整输入节点与隐层节点的联接强度和隐层节点与输出节点的联接强度以及阈值，使误差沿梯度方向下降，经过反复学习训练，确定与最小误差相对应的网络参数(权值和阈值)，训练即告停止。此时经过训练的神经网络即能对类似样本的输入信息，自行处理输出误差最小的经过非线形转换的信息。

bp神经网络的神经元

神经网络是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的。
神经网络由多个神经元构成，下图就是单个神经元的图1所示：
在这里插入图片描述
。。。。。。。。。。。。。。。。。。。。。。。。图1 ，神经元模型

bp神经网络激活函数及公式

在这里插入图片描述
![在这里插入图片描述](https://img-blog.csdnimg.cn/29edde342c3945939ad5945145ca8509.png在这里插入图片描述

BP神经网络传递函数及公式

图2是Sigmoid函数和双极S函数的图像，其中Sigmoid函数的图像区域是0到1，双极S函数的区间是正负1，归一化的时候要和传递函数的区域相对应，不然，可能效果不好
神经网络就是将许多个单一的神经元联结在一起，这样，一个神经元的输出就可以是另一个神经元的输入。
例如，下图就是一个简单的神经网络：在这里插入图片描述
在这里插入图片描述

麻雀算法SSA的原理

主要公式

在SSA中，具有较好适应度值的发现者在搜索过程中会优先获取食物。此外，因为发现者负责为整个麻雀种群寻找食物并为所有加入者提供觅食的方向。因此，发现者可以获得比加入者更大的觅食搜索范围。在每次迭代的过程中，发现者的位置更新描述如下：
在这里插入图片描述
其中，t代表当前迭代数，itermax是一个常数，表示最大的迭代次数。Xij表示第i个麻雀在第j维中的位置信息。α∈(0,1]是一个随机数。R2(R2∈[0,1])和ST(ST∈[0.5,1])分别表示预警值和安全值。Q是服从正态分布的随机数。L表示一个1×d的矩阵，其中该矩阵内每个元素全部为1。当R2< ST 时，这意味着此时的觅食环境周围没有捕食者，发现者可以执行广泛的搜索操作。当R2 ≥ ST，这表示种群中的一些麻雀已经发现了捕食者，并向种群中其它麻雀发出了警报，此时所有麻雀都需要迅速飞到其它安全的地方进行觅食。
加入者（追随者）的位置更新描述如下：
在这里插入图片描述

其中，Xp是目前发现者所占据的最优位置，Xworst则表示当前全局最差的位置。A表示一个1×d的矩阵，其中每个元素随机赋值为1或-1，并且A+=AT(AAT)-1。当i >n/2时，这表明，适应度值较低的第i个加入者没有获得食物，处于十分饥饿的状态，此时需要飞往其它地方觅食，以获得更多的能量。
当意识到危险时，麻雀种群会做出反捕食行为，其数学表达式如下：
在这里插入图片描述

其中，其中Xbest是当前的全局最优位置。β作为步长控制参数，是服从均值为0，方差为1的正态分布的随机数。K∈[-1,1]是一个随机数，fi则是当前麻雀个体的适应度值。fg和fw分别是当前全局最佳和最差的适应度值。ε是最小的常数，以避免分母出现零。
为简单起见，当fi >fg表示此时的麻雀正处于种群的边缘，极其容易受到捕食者的攻击。fi = fg时，这表明处于种群中间的麻雀意识到了危险，需要靠近其它的麻雀以此尽量减少它们被捕食的风险。K表示麻雀移动的方向同时也是步长控制参数。

麻雀算法SSA的主要参数：

一、种群个数popsize，既算法中麻雀的个数；
二、最大迭代次数maxgen，既算法迭代gen次后停止迭代；
三、种群维度dim，既需要优化的自变量个数；
四、种群位置pop，既每个麻雀的对应的自变量的值，一个麻雀对应一组自变量，相当于一个解；
五、发现者比例P_percent，既麻雀算法发现者占所有麻雀的比例；
六、安全值ST，既这意味着此时的觅食环境周围没有捕食者；

麻雀算法流程图

在这里插入图片描述
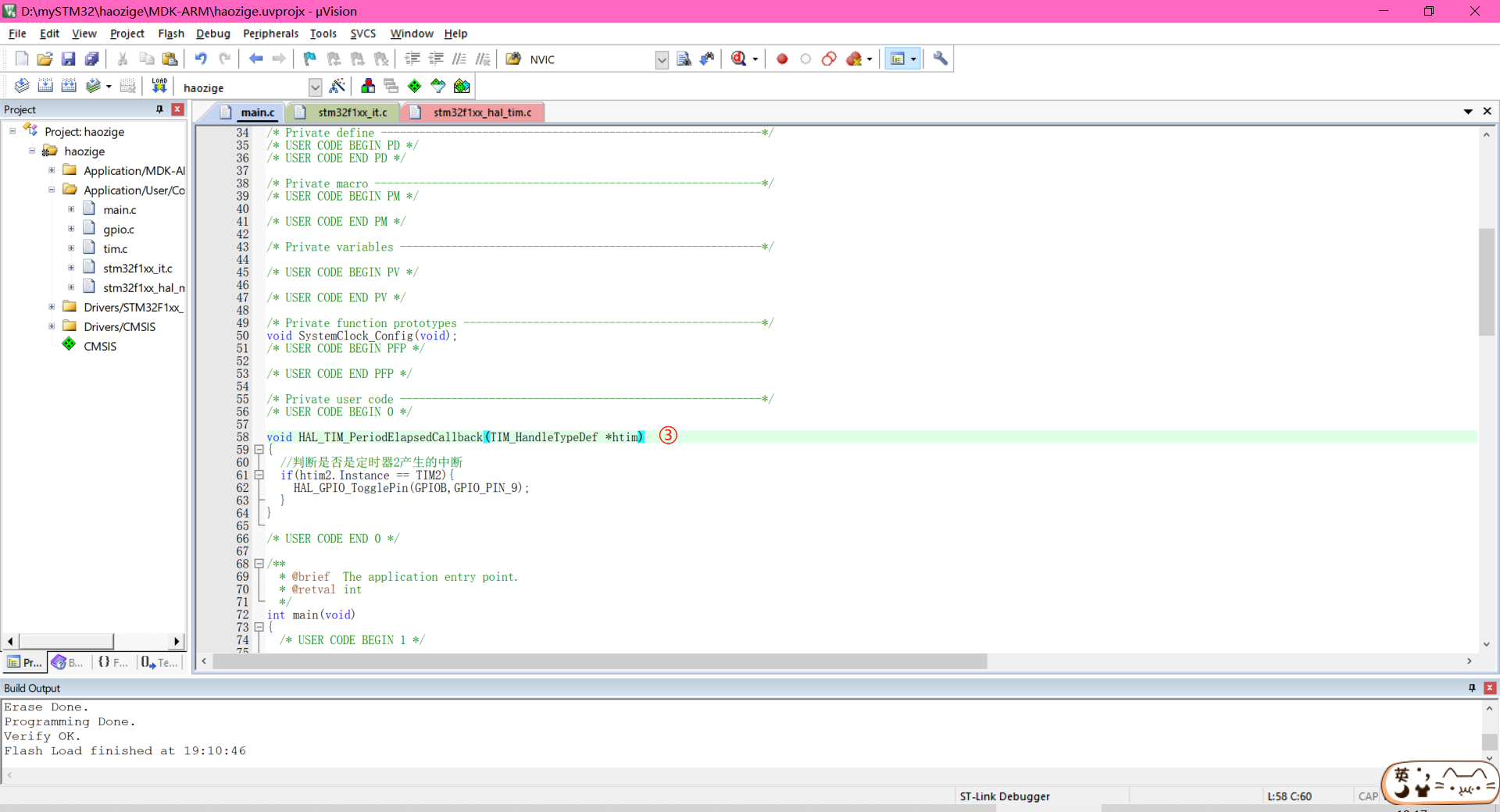
基于麻雀算法改进 的B神经网络坑基监测

神经网络参数

三层神经网络，传递函数logsig ， tansig，训练函数自适应动量因子梯度下降函数，学习率0.1，学习目标0.001，最大迭代次数1000

麻雀算法的主要参数

MATLAB编程代码

% 清空环境
clc
clear
close all
warning off
%读取数据
[num ,ax,ay]= xlsread(‘基坑监测数据改后.xls’);
num(:,[3 6]) = [];
npan =2;%选择第一列数据

if npan<5
num1 = num(:,npan);
n1 = length(num1);
m1 = 5;
num2 = zeros(n1-m1,m1+1);
for ii = 1:n1-m1
num2(ii,:) = num1(ii:ii+m1)‘;
end
else
num1 = num(1:2:end,npan);
n1 = length(num1);
m1 = 5;
num2 = zeros(n1-m1,m1+1);
for ii = 1:n1-m1
num2(ii,:) = num1(ii:ii+m1)’;
end
end

%节点个数
inputnum=m1;
hiddennum=10;
outputnum=1;
m = round(0.8*length(num2));
n = randperm(length(num2));
%训练数据和预测数据
input_train=num2(n(1:m),1:m1)‘;
input_test=num2(m+1:end,1:m1)’;
output_train=num2(n(1:m),m1+1)‘;
output_test=num2(m+1:end,m1+1)’;

%选连样本输入输出数据归一化
[inputn,inputps]=mapminmax(input_train);
[outputn,outputps]=mapminmax(output_train);

%构建网络
% net=newff(inputn,outputn,hiddennum);
net = newff(minmax(inputn),[10,1],{‘logsig’,‘tansig’},‘traingdx’);
[BPoutput,errorb] = bpp(input_train,input_test,output_train,output_test);
% 参数初始化
dim=inputnumhiddennum+hiddennum+hiddennumoutputnum+outputnum;
maxgen=30; % 进化次数
sizepop=20; %种群规模

popmax=5;
popmin=-5;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
P_percent = 0.2; % The population size of producers accounts for “P_percent” percent of the total population size

pNum = round( sizepop * P_percent ); % The population size of the producers

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i=1:sizepop
pop(i,:)=5*rands(1,dim);
% V(i,:)=rands(1,21);
fitness(i)=fun(pop(i,:),inputnum,hiddennum,outputnum,net,inputn,outputn);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
pFit = fitness;
[ fMin, bestI ] = min( fitness ); % fMin denotes the global optimum fitness value
bestX = pop( bestI, : ); % bestX denotes the global optimum position corresponding to fMin

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%麻雀搜索算法 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for t = 1 : maxgen
[ ans, sortIndex ] = sort( pFit );% Sort.

[fmax,B]=max( pFit );
worse= pop(B,:);

r2=rand(1);
if(r2<0.8)

for i = 1 : pNum                                                   % Equation (3)
     r1=rand(1);
    pop( sortIndex( i ), : ) = pop( sortIndex( i ), : )*exp(-(i)/(r1*maxgen));
   
    fitness(sortIndex( i ))=fun(pop(sortIndex( i ),:),inputnum,hiddennum,outputnum,net,inputn,outputn); 
end

else
for i = 1 : pNum

pop( sortIndex( i ), : ) = pop( sortIndex( i ), : )+randn(1)*ones(1,dim);

fitness(sortIndex( i ))=fun(pop(sortIndex( i )😅,inputnum,hiddennum,outputnum,net,inputn,outputn);

end

end
[ fMMin, bestII ] = min( fitness );
bestXX = pop( bestII, : );
for i = ( pNum + 1 ) : sizepop % Equation (4)

     A=floor(rand(1,dim)*2)*2-1;
     
      if( i>(sizepop/2))
       pop( sortIndex(i ), : )=randn(1)*exp((worse-pop( sortIndex( i ), : ))/(i)^2);
      else
      pop( sortIndex( i ), : )=bestXX+(abs(( pop( sortIndex( i ), : )-bestXX)))*(A'*(A*A')^(-1))*ones(1,dim);  

     end  
    
    fitness(sortIndex( i ))=fun(pop(sortIndex( i ),:),inputnum,hiddennum,outputnum,net,inputn,outputn);

end
c=randperm(numel(sortIndex));
b=sortIndex(c(1:3));
for j = 1 : length(b) % Equation (5)

if( pFit( sortIndex( b(j) ) )>(fMin) )

    pop( sortIndex( b(j) ), : )=bestX+(randn(1,dim)).*(abs(( pop( sortIndex( b(j) ), : ) -bestX)));

    else

    pop( sortIndex( b(j) ), : ) =pop( sortIndex( b(j) ), : )+(2*rand(1)-1)*(abs(pop( sortIndex( b(j) ), : )-worse))/ ( pFit( sortIndex( b(j) ) )-fmax+1e-50);

end
   
   
   fitness(sortIndex( i ))=fun(pop(sortIndex( i ),:),inputnum,hiddennum,outputnum,net,inputn,outputn);
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
for i = 1 : sizepop
if ( fitness( i ) < pFit( i ) )
pFit( i ) = fitness( i );
pop(i,:) = pop(i,:);
end

    if( pFit( i ) < fMin )
       fMin= pFit( i );
        bestX =pop( i, : );
     
        
    end
end



yy(t)=fMin;

end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% 迭代寻优
x=bestX
%% 结果分析
plot(yy)
title(['适应度曲线 ’ ‘终止代数＝’ num2str(maxgen)]);
xlabel(‘进化代数’);ylabel(‘适应度’);
%% 把最优初始阀值权值赋予网络预测
% %用麻雀搜索算法优化的BP网络进行值预测
w1=x(1:inputnumhiddennum);
B1=x(inputnumhiddennum+1:inputnumhiddennum+hiddennum);
w2=x(inputnumhiddennum+hiddennum+1:inputnumhiddennum+hiddennum+hiddennumoutputnum);
B2=x(inputnumhiddennum+hiddennum+hiddennumoutputnum+1:inputnumhiddennum+hiddennum+hiddennumoutputnum+outputnum);

net.iw{1,1}=reshape(w1,hiddennum,inputnum);
net.lw{2,1}=reshape(w2,outputnum,hiddennum);
net.b{1}=reshape(B1,hiddennum,1);
net.b{2}=B2;

%% 训练
%网络进化参数
net.trainParam.epochs=5000;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001;

%网络训练
[net,tr]=train(net,inputn,outputn);

%%预测
%数据归一化
inputn_test=mapminmax(‘apply’,input_test,inputps);
an=sim(net,inputn_test);
test_simu=mapminmax(‘reverse’,an,outputps);
error=test_simu-output_test;

figure
plot(test_simu,‘r-o’)
hold on
plot(BPoutput,‘b-s’)
hold on
plot(output_test,‘k-*’)
hold off
xlabel(‘样本’)
ylabel(‘土体倾斜’)
ylim([32 40])
legend(‘ssa-bp’,‘bp’,‘实际值’)

figure
plot(error)
title(‘仿真预测误差’,‘fontsize’,12);
xlabel(‘仿真次数’,‘fontsize’,12);ylabel(‘误差百分值’,‘fontsize’,12);

效果图

在这里插入图片描述
在这里插入图片描述

结果分析

从效果图上看，麻雀算法改进的BP神经网络能够实现对基坑数据的预测，意味能提前预判存在的风险，提前采取预防和纠正措施，比传统的实时监测更有实用意义，对风险管控更好，有疑问或者其他应用方面，欢迎大家扫描下面的二维码

展望

针对神经网络供工具箱，可以自己写函数的代入并原本的工具箱函数，可以有很多种改进方法

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/381698.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

matlab-数据和数据运算

matlab-数据和数据运算

学习视频基本数据类型1.1 整型与浮点型在matlab中同样有8、16、32、64bit的数据大小之分&#xff0c;同时也可以叠加signed(有符号)和unsigned(无符号)的区别&#xff0c;默认数据类型为double(双精度浮点型)参考其他博客的详述1.2 复数还有一些其他常用的函数方法&#xff1a;…
阅读更多...
STM32之定时器

STM32之定时器

定时器软件定时缺点&#xff1a;不精确&#xff0c;占用CPU资源定时器工作原理使用精准的时基&#xff0c;通过硬件的方式&#xff0c;实现定时功能。定时器的核心是计数器。通用定时器框图该框图主要分成四部分&#xff1a;时钟产生器、时基单元、输入捕获、输出比较时钟产生器…
阅读更多...
springboot通过aop实现全局日志(是否自定义注解都可以)

springboot通过aop实现全局日志(是否自定义注解都可以)

内容参考自以下两个链接1、springboot中使用AOP切面完成全局日志_aop全局日志_邹飞鸣的博客-CSDN博客使用AOP记录日志_aop日志_trusause的博客-CSDN博客第一个链接思路很清晰,讲的也很详细,第二个链接讲了自定义注解为了便于自己理解做了以下整理目录 1.aspectj基本概念 2.添加…
阅读更多...
闪光桐人の实习日记（2023年2月27日-3月3日）

闪光桐人の实习日记（2023年2月27日-3月3日）

前往闪闪の小窝以获得更好的阅读和评论体验 文章目录2023年3月2日&#xff08;测试流程&#xff09;为什么是什么如何进行2023年3月1日&#xff08;消息队列MQ&#xff09;什么是消息队列为什么要使用消息队列消息队列&#xff08;kafka&#xff09;的优势关键信息SpringBoot整…
阅读更多...
LeetCode题目笔记——448. 找到所有数组中消失的数字

LeetCode题目笔记——448. 找到所有数组中消失的数字

文章目录题目描述题目链接题目难度——简单方法一&#xff1a;使用额外空间&#xff0c;字典代码/Python代码/C方法二&#xff1a;进阶&#xff0c;原地修改代码/C代码/C总结题目描述 这好像是一到经典的面试题 给你一个含 n 个整数的数组 nums &#xff0c;其中 nums[i] 在区间…
阅读更多...
遮挡检测--基于角度的遮挡检测方法

遮挡检测--基于角度的遮挡检测方法

文章目录1基于角度的遮挡检测方法2遮挡检测遍历方法2.1方法1--自适应径向扫描方法2.2方法2--螺旋扫描法参考1基于角度的遮挡检测方法 在基于角度的方法中&#xff0c;通过依次分析DSM中沿径向方向的投影光线的角度来识别遮挡。定义α\alphaα角&#xff1a;DSM三维点与相机中心…
阅读更多...
解决Windows虚拟机启动资源占用过多

解决Windows虚拟机启动资源占用过多

由于虚拟机中的Windows一般是指定版本的&#xff0c;创建后&#xff0c;其自身仍在不断自动更新&#xff0c;因此这里我们禁用两个服务&#xff0c;以后启动Windows之后就不会占用太多资源了&#xff1a; 禁用setuphost.exe禁用.net runtime optimization 文章目录1. 禁用setu…
阅读更多...
分布式定时任务-学习笔记

分布式定时任务-学习笔记

1 发展历程 1.1 Linux命令-CronJob 只能控制单台机器 1.2 任务调度-Quartz 单任务极致控制 1.3 分布式定时任务 1.3.1 定时任务 系统为了自动完成特定任务&#xff0c;实时、延时、周期性完成任务调度的过程 1.3.2 分布式定时任务 把分散的、可靠性差的定时任务纳入统一的平…
阅读更多...
VScode下 ESP32 下载程序

VScode下 ESP32 下载程序

ESP32-S3 下载方式可以通过UART0 下载,USB 下载&#xff0c;JTAG下载,还可以使用WIFI进行远程OTA升级程序。插件底栏按键介绍&#xff1a;①选择串口端口号&#xff0c;如COM3&#xff1b; ②选择芯片型号&#xff1b; ③工程idf设置&#xff0c;相当于menuconfig&#xff1b; …
阅读更多...
Redis缓存雪崩、缓存击穿、缓存穿透

Redis缓存雪崩、缓存击穿、缓存穿透

用户的数据一般都是存储于数据库&#xff0c;数据库的数据是落在磁盘上的&#xff0c;磁盘的读写速度可以说是计算机里最慢的硬件了。 当用户的请求&#xff0c;都访问数据库的话&#xff0c;请求数量一上来&#xff0c;数据库很容易就奔溃的了&#xff0c;所以为了避免用户直…
阅读更多...
【Java】Spring Boot 日志文件

【Java】Spring Boot 日志文件

文章目录SpringBoot日志文件1. 日志有什么用2. 日志怎么用3. 自定义日志打印3.1 在程序中得到日志对象3.2 使用日志对象打印日志4. 日志级别4.1 日志级别有什么用&#xff1f;4.2 日志级别的分类与使用5. 日志持久化6. 更简单的日志输出--lombok6.1 添加 lombok 依赖6.2 输出日…
阅读更多...
操作系统真相还原——第6章内存管理系统

操作系统真相还原——第6章内存管理系统

第八章 内存管理系统 makefile 编译整个项目&#xff0c;如果改变局部关系&#xff0c;只靠人工难以维护文件间的依赖关系&#xff0c;所以通过make程序进行处理 makefile文件是make程序的搭档&#xff1a;发现某个文件更新后&#xff0c;只编译该文件和受该文件影响的相关文…
阅读更多...
为什么95%的Java程序员人，都是用不好Synchronized？

为什么95%的Java程序员人，都是用不好Synchronized？

Synchronized锁优化 jdk1.6对锁的实现引入了大量的优化&#xff0c;如自旋锁、适应性自旋锁、锁消除、锁粗化、偏向锁、轻量级锁等技术来减少锁操作的开销。 锁主要存在四中状态&#xff0c;依次是&#xff1a;无锁-> 偏向锁 -> 轻量级锁 -> 重量级锁&#xff0c;他们…
阅读更多...
upload-labs通关详细教程

upload-labs通关详细教程

文章目录文件上传要点1、前端验证绕过做题步骤源码分析2、Content-Type方式绕过做题步骤源码分析3、黑名单绕过做题步骤源码分析4、.htaccess文件绕过简介做题步骤源码分析5、后缀大小写绕过简介做题步骤源码分析6、文件后缀&#xff08;空&#xff09;绕过简介做题步骤源码分析…
阅读更多...
CAN工具-VSpy(ValueCAN) - Panel面板（续）

CAN工具-VSpy(ValueCAN) - Panel面板（续）

继续上次的Panel面板介绍&#xff01;&#xff01;&#xff01;7. LED 控件LED控件可以用作指示器。在Graphical Panels中选中该控件&#xff0c;在界面右侧侧拉框的Properties中可设置LED控件的通用属性。LED控制属性LED On Color&#xff1a;双击打开标准的Windows颜色选择器…
阅读更多...
Vue 3.0 学习笔记之基础知识

Vue 3.0 学习笔记之基础知识

系列文章目录 提示&#xff1a;阅读本章之前&#xff0c;请先阅读目录 文章目录系列文章目录前言Vue 3.0 创建与Vue2.0对比的变化关闭语法检查setup 组合式函数compositions前言 Vue 3.0 创建 与Vue2.0对比的变化 关闭语法检查 lintOnSave: false setup 组合式函数compositions…
阅读更多...
Git 初体验 (处理 .ssh 文件的相关问题)

Git 初体验 (处理 .ssh 文件的相关问题)

目录前沿环境入门教程出现的问题问题 1 &#xff1a;C 盘用户文件中找不到 .ssh 文件问题 2 : 在 clone 远程仓库文件时报错问题3 : 第一次从 Gitee clone 项目时会弹出一个 Git 窗口,要你输入用户和密码获取 credential (可以信任的证明)自我实践总结引用前沿 很早前安装了 G…
阅读更多...
二叉树——删除二叉搜索树中的节点

二叉树——删除二叉搜索树中的节点

删除二叉搜索树中的节点 链接 给定一个二叉搜索树的根节点 root 和一个值 key&#xff0c;删除二叉搜索树中的 key 对应的节点&#xff0c;并保证二叉搜索树的性质不变。返回二叉搜索树&#xff08;有可能被更新&#xff09;的根节点的引用。 一般来说&#xff0c;删除节点可…
阅读更多...
2022_SPL_CMINet

2022_SPL_CMINet

Cross-Stage Multi-Scale Interaction Network for RGB-D Salient Object Detection 用于rgb-d显着目标检测的跨阶段多尺度交互网络 目录 文章目录 前言 一、引言 二、提出的方法 A.概述 感觉有点乱&#xff0c;没看太懂&#xff0c;没关系&#xff0c;我们接着往下看 …
阅读更多...
Postman 实现 UI 自动化测试

Postman 实现 UI 自动化测试

看到这篇文章的标题&#xff0c;是不是有小伙伴会感到惊讶呢&#xff1f; Postman 不是做接口测试的吗&#xff1f;为什么还能做 UI 自动化测试呢&#xff1f; 其实&#xff0c;只要你了解 Selenium 的运行原理&#xff0c;就可以理解为什么 Postman 也能实现 UI 自动化测试了…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023