文章目录
- 前言
- 知识框架
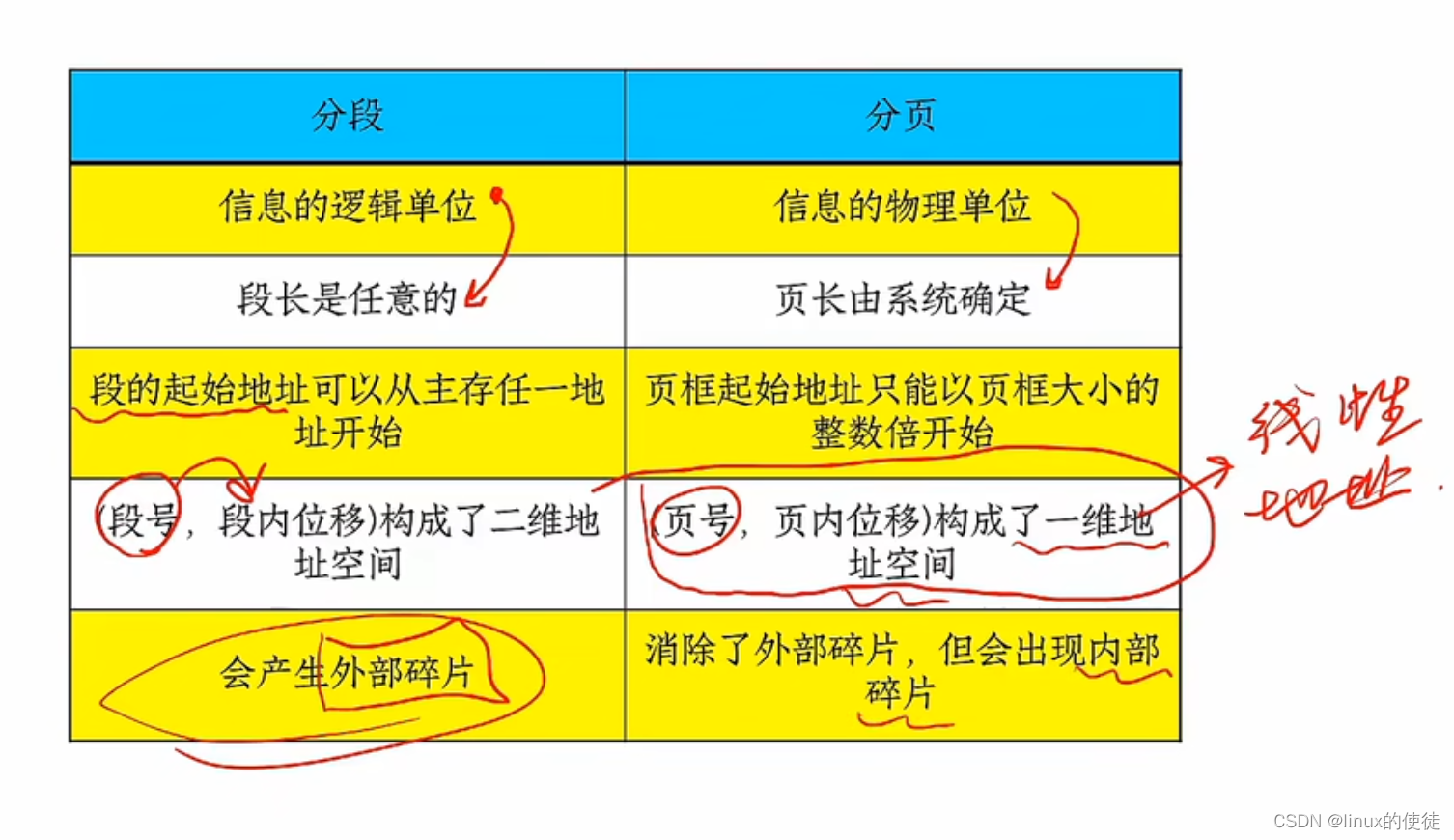
- 数据结构的区分
- 1. 图的基本概念
- 1.1 图的定义
- 1.2 图的基本概念和术语
- 总结
前言
参考文献：数据结构：图(Graph)【详解】
知识框架
数据结构的区分
线性表：数据元素之间是被串起来的，仅有线性关系，每个数据元素只有一个直接前驱和一个直接后继。
树：数据元素之间有着明显的层次关系，并且每一层上的数据元素可能和下一层中多个元素相关，但只能和上一层中一个元素相关。
图：结点之间的关系可以是任意的，图中任意两个数据元素之间都可能相关。
1. 图的基本概念
1.1 图的定义
图G由顶点集V和边集E组成，记为G=（V，E），其中V(G)表示图G中顶点的有限非空集；E(G)表示图G中顶点之间的关系（边）集合。若 V = v 1 , v 2 , … , v n V={v_1,v_2,…,v_n} V=v1,v2,…,vn，则用|V|表示图G中顶点的个数，也称图G的阶， E = ( u , v ) ∣ u ∈ V , v ∈ V E={(u,v)|u\in V,v\in V} E=(u,v)∣u∈V,v∈V，用|E|表示图G中边的条数。
注：
- 线性表可以是空表，树可以是空树，但图不可以是空图。
- 图中不能一个顶点也没有，图的顶点集V一定非空，但边集E可以为空，此时图中只有顶点而没有边。
1.2 图的基本概念和术语
1. 有向图
若E是有向边(也称弧)的有限集合时，则图G为有向图。弧是顶点的有序对，记为<v, w>，其中v,w是顶点，v称为弧尾，w称为弧头，<v,w>称为从顶点v到顶点w的弧，也称v邻接到w，或w邻接自v。
图(a)所示的有向图
G
1
G_1
G1可表示为:
G
1
=
(
V
1
,
E
1
)
V
1
=
{
1
,
2
,
3
}
E
1
=
{
<
1
,
2
>
,
<
2
,
1
>
,
<
2
,
3
>
}
G_1 =(V_1,E_1)\\ V_1 = \{1,2,3\}\\ E_1=\{<1,2>,<2,1>,<2,3>\}\\
G1=(V1,E1)V1={1,2,3}E1={<1,2>,<2,1>,<2,3>}
2. 无向图
若E是无向边(简称边)的有限集合时，则图G为无向图。边是顶点的无序对，记为(v, w)或(w,v),因为(v,w)=(w,v), 其中v,w是顶点。可以说顶点w和顶点v互为邻接点。边(v, w)依附于顶点w和v，或者说边(v, w)和顶点v, w相关联。
图(b)所示的无向图G2可表示为:
G
2
=
(
V
2
,
E
2
)
V
2
=
{
1
,
2
,
3
,
4
}
E
2
=
{
(
1
,
2
)
,
(
1
,
3
)
,
(
1
,
4
)
,
(
2
,
3
)
,
(
2
,
4
)
,
(
3
,
4
)
}
G_2 =(V_2,E_2)\\ V_2 = \{1,2,3,4\}\\ E_2=\{(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)\}
G2=(V2,E2)V2={1,2,3,4}E2={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
3. 简单图
一个图 G若满足不存在重复边,不存在顶点到自身的边则称图G为简单图。
上图中 G 1 G_1 G1和 G 2 G_2 G2均为简单图,数据结构中仅讨论简单图。
总结
提示：这里对文章进行总结：
例如：以上就是今天要讲的内容，本文仅仅简单介绍了pandas的使用，而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。
