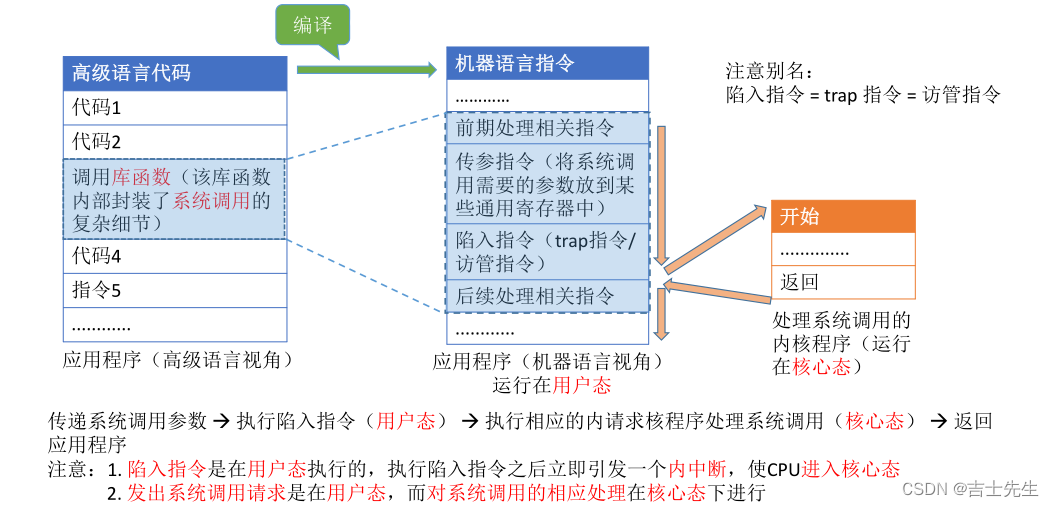
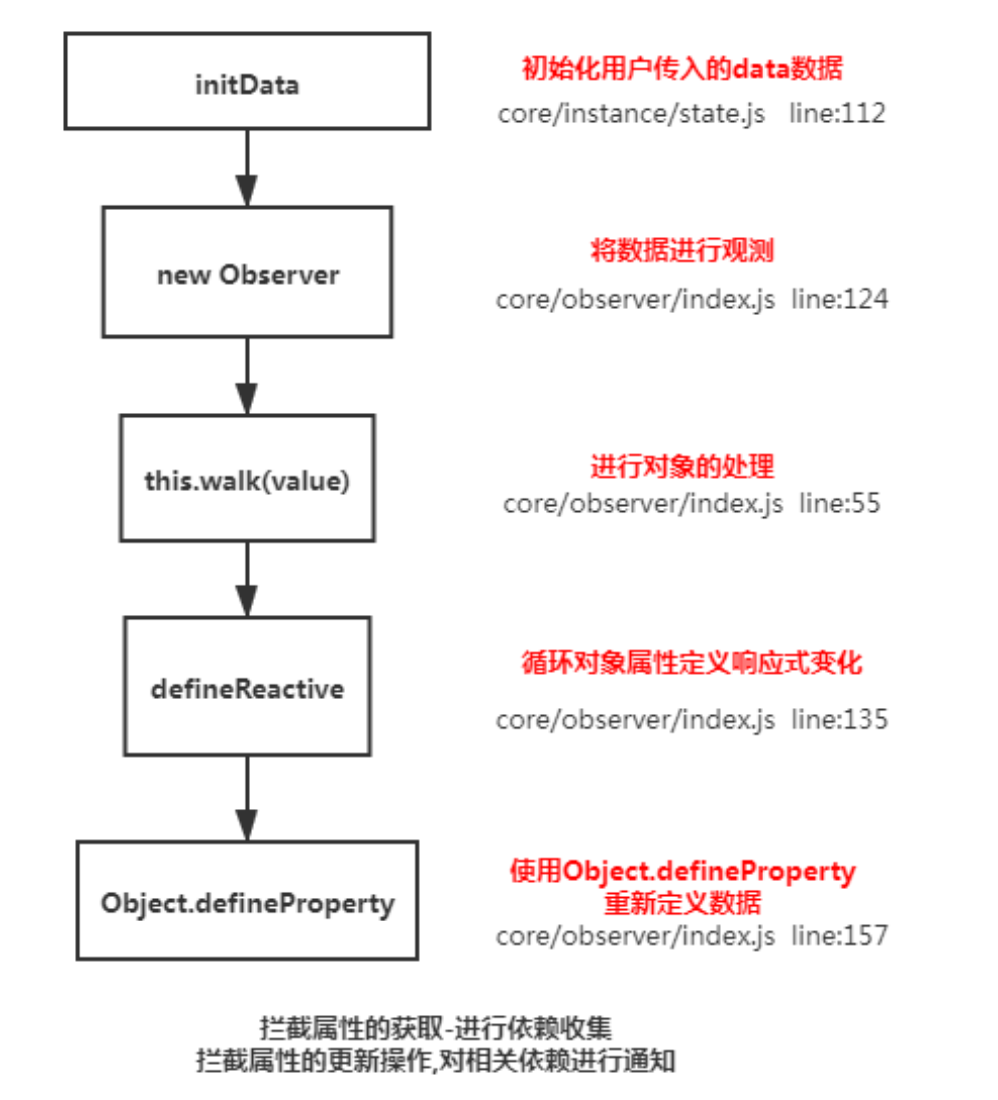
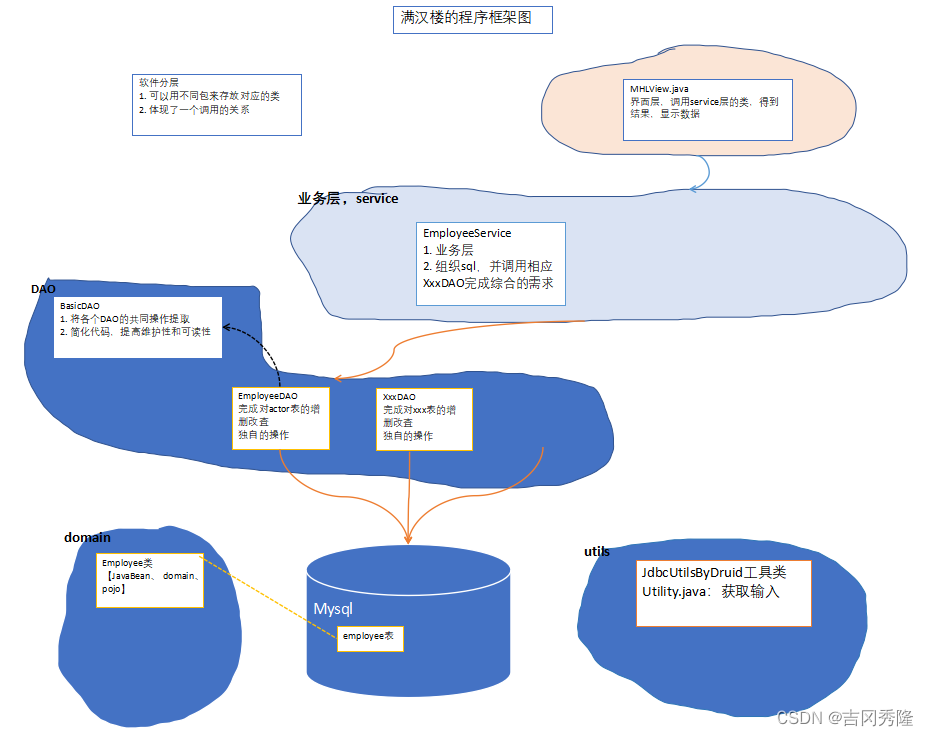
1. 满汉楼
1.结构图
2. 数据库
pwd CHAR(32) NOT NULL DEFAULT ‘’,# 密码,32位
INSERT INTO employee VALUES(NULL, ‘666’, MD5(‘123456’), ‘老韩’, ‘经理’);
MD5(‘123456’)是经过MD5加密过后的32位的字符串,用来保存密码
select * from employee where empId = ? and pwd = MD5(?);#查询时也要加上MD5()
确保:把业务层的sql语句放到数据库查询分析器测试一下
return update > 0;简便写法
javabean中需要有无参构造器和settter方法,来供底层反射调用
一个DAO对应一个JavaBean,对应一个Service,业务层之间可以相互合作;
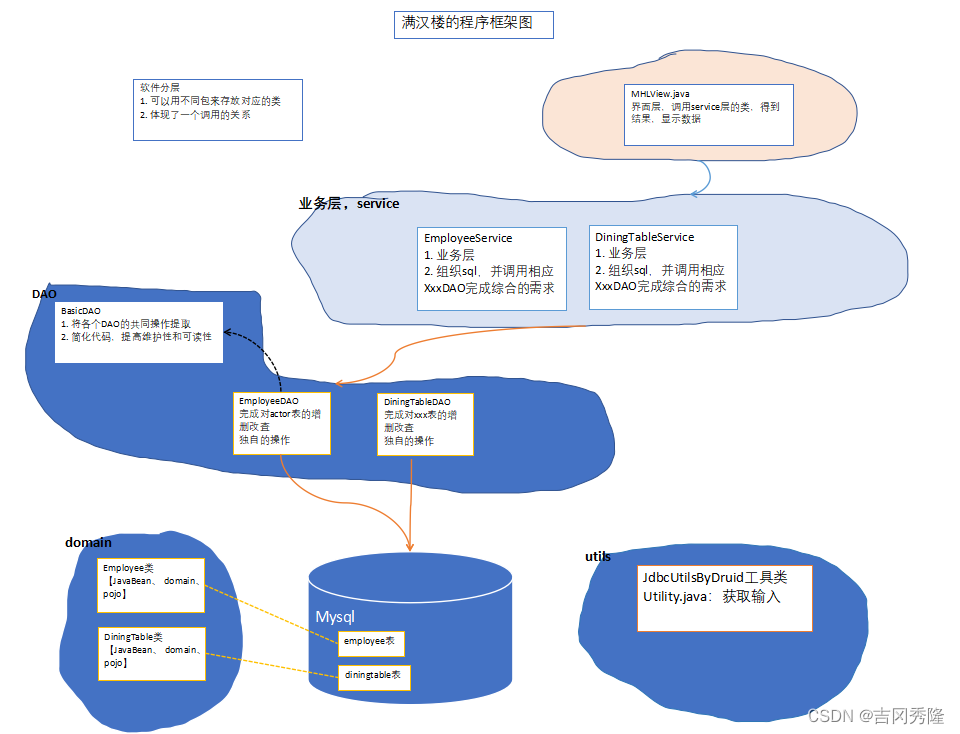
3. 预定餐桌
- 餐桌号是否存在,餐桌存在是否已被人预定;
- 更新餐桌信息(状态,联系方式,预定人姓名);
4. 点餐服务
- 在哪个桌子上点餐(桌号要存在),点哪个菜(菜品号要存在),点多少份;
- 更新桌子状态信息为 就餐中;
- 生成账单记录,在BillService中完成主要业务;
5. 结账
- 选择结账的餐桌号,餐桌号是否存在;
6. DBUtils底层用到反射
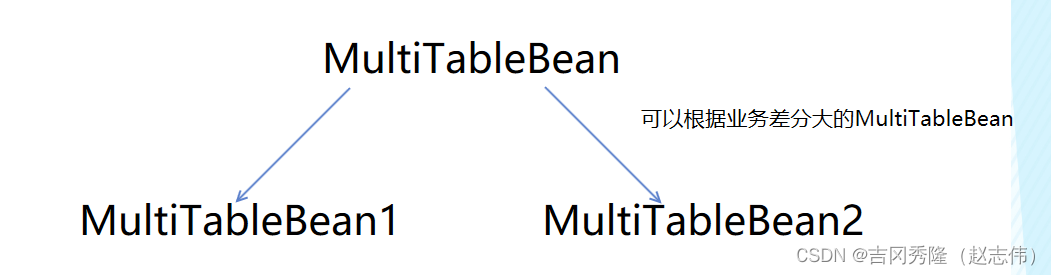
javabean中的属性和必须和数据库表里查询出的表明一致,如果MultiTableBean中的属性有冲突,可以在查询的时候给表里的字段起别名;


2. 马踏棋盘
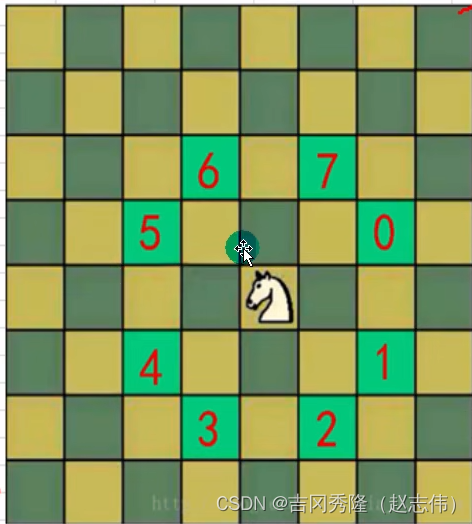
骑士周游算法
- 创建6x6的棋盘,是二维数组
- 将当前位置设置为已经访问过,根据当前位置计算马儿还能走哪些位置,并放入到一个集合(ArrayList)中,最多有8个,每走一步,setp+1
- 遍历ArrayList中存放的所有位置,看看哪个可以走,如果可以走得通,就继续,如果走不通,就回溯
- 判断马儿是否完成了任务,使用step和应该走的步数比较,如果没有达到数量,则表示没有完成任务,就将整个棋盘设置为0
public class HorseChessBoard {
//定义属性
private static int X = 6;//代表 col
private static int Y = 6;//代表 row
private static int[][] chessBoard = new int[X][Y];//棋盘
private static boolean[] visited = new boolean[X * Y];//记录某个位置是否走过
private static boolean finished = false;//记录马儿是否遍历完棋盘
public static void main(String[] args) {
int row = 6;//6行
int col = 3;//6列
//进行测试
travelsalChessBoard(chessBoard, row - 1, col - 1, 1);
//输出当前棋盘的情况
for (int[] rows : chessBoard) {
for (int step : rows) {//step 表示 这是马儿应该走的第几步
System.out.print(step + "\t");
}
System.out.println();
}
}
//编写核心算法,遍历棋盘,如果遍历成功,就把 finished 设置为true
//并且,将马儿走的每一步step,记录到 chessBoard
public static void travelsalChessBoard(int[][] chessBoard, int row, int col, int step) {
//将step记录到chessBoard
chessBoard[row][col] = step;
//将当前位置设置为已经访问
visited[row * X + col] = true;
//获取当前位置可以走的下一个位置有哪些
ArrayList<Point> ps= next(new Point(col, row));//col - X, row - Y
//遍历
while (!ps.isEmpty()) {
//取出集合中的第一个点(位置)
Point p = ps.remove(0);
//判断该位置是否走过,如果没有走过,就递归遍历
if (!visited[p.y * X + p.x]) {
//递归
travelsalChessBoard(chessBoard, p.y, p.x, step + 1);
}
}
//当退出while循环,看看是否遍历成功
if (step < X * Y && !finished) {
//如果遍历不成功,就回溯,同时重置棋盘
chessBoard[row][col] = 0;
visited[row * X + col] = false;
} else {
finished = true;
}
}
//编写方法,获取当前位置可以走的下一步的所有位置(Point表示 坐标x,y)
public static ArrayList<Point> next(Point curPoint) {
//创建集合,存放所有可以走的点
ArrayList<Point> points = new ArrayList<>();
//创建一个Point对象,点/一个位置,如果坐标匹配则放入到集合中
Point p1 = new Point();
//根据题目要求,判断在 curPoint点 是否可以走如下位置,如果可以走,就将该点(Point)放入到集合
//判断是否可以走5位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
points.add(new Point(p1));
}
//判断是否可以走6位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
points.add(new Point(p1));
}
//判断是否可以走7位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {
points.add(new Point(p1));
}
//判断是否可以走0位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
points.add(new Point(p1));
}
//判断是否可以走1位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
points.add(new Point(p1));
}
//判断是否可以走2位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
points.add(new Point(p1));
}
//判断是否可以走3位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
points.add(new Point(p1));
}
//判断是否可以走4位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
points.add(new Point(p1));
}
return points;
}
}
2.1 创建棋盘
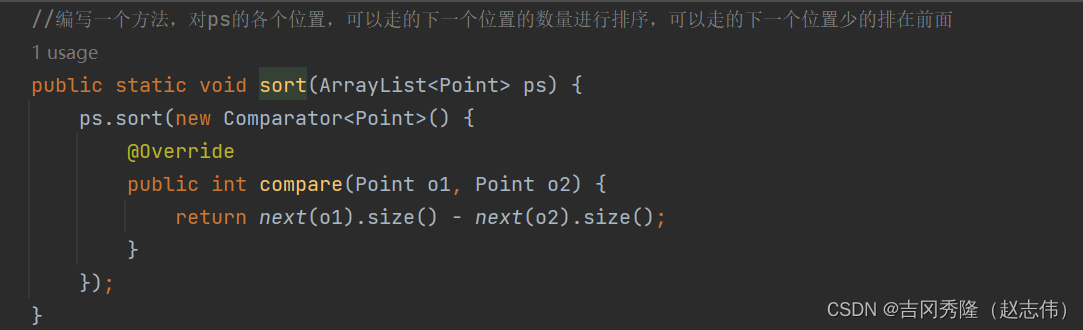
2.2 穷尽所有的位置
2.3 递归遍历回溯
2.4 贪心算法优化