文章目录
- 一:标量和向量
- (1)基本概念
- (2)坐标系中的向量表示
- 二:向量运算
- (1)加减与数乘
- (2)向量内积
- A:为什么需要向量内积
- B:向量内积
- C:柯西-施瓦茨不等式
- (3)线性组合
- 三:基向量和向量空间(线性空间)
- (1)基向量
- (2)向量张成的空间
- (3)特征向量与特征空间
- 五:向量线性相关性
- (1)数学角度解释
- (2)空间角度解释
一:标量和向量
(1)基本概念
标量:由单一数值构成的对待研究对象的量化评价,标量的定义与其代表的数据类型强相关
- 用单位
cm的实数值表示身高 - 用取值为
0或1的布尔型值表示信用状况
向量:如果在标定或描述一个事物的特征时需要用到多个标量,那么它就称之为向量
- 物体的颜色是一个向量(RGB)
- 空间位置是一个向量
给定任一向量 x = [ x 1 , x 2 , . . . , x d ] x=[x_{1},x_{2},...,x_{d}] x=[x1,x2,...,xd],它包含大小与方向两类信息,只有各分量位置处取相同值时两个向量才相等
- 大小:是指所有分量的平方和的根号,也即 ∣ ∣ x ∣ ∣ = ∑ i = 1 d x i 2 ||x||=\sqrt{\sum\limits_{i=1}^{d}x_{i}^{2}} ∣∣x∣∣=i=1∑dxi2
- 方向:是向量不同分量之间的比值
若有集合 s = { 1 , 3 , 5 } s=\{1,3,5\} s={1,3,5},则
- x s = { x 1 , x 3 , x 5 } x_{s}=\{x_{1},x_{3},x_{5}\} xs={x1,x3,x5}
- x − s = { x 2 , x 4 , x 6 , . . . , x d } x_{-s}=\{x_{2},x_{4},x_{6},...,x_{d}\} x−s={x2,x4,x6,...,xd}
注意以下特殊向量
- 零向量: [ 0 , 0 , . . . , 0 ] [0,0,...,0] [0,0,...,0]
- 单位向量 e e e: [ x 1 ∣ ∣ x ∣ ∣ , x 2 ∣ ∣ x ∣ ∣ , . . . x d ∣ ∣ x ∣ ∣ ] [\frac{x_{1}}{||x||},\frac{x_{2}}{||x||},...\frac{x_{d}}{||x||}] [∣∣x∣∣x1,∣∣x∣∣x2,...∣∣x∣∣xd]
- 转置 x T x^{T} xT: 此时行向量变列向量;列向量变行向量
(2)坐标系中的向量表示
坐标系中的向量表示:在线性代数中,向量是一个以坐标原点为起点的箭头
- 下图是二维平面直角坐标系,三维或更高维也是如此
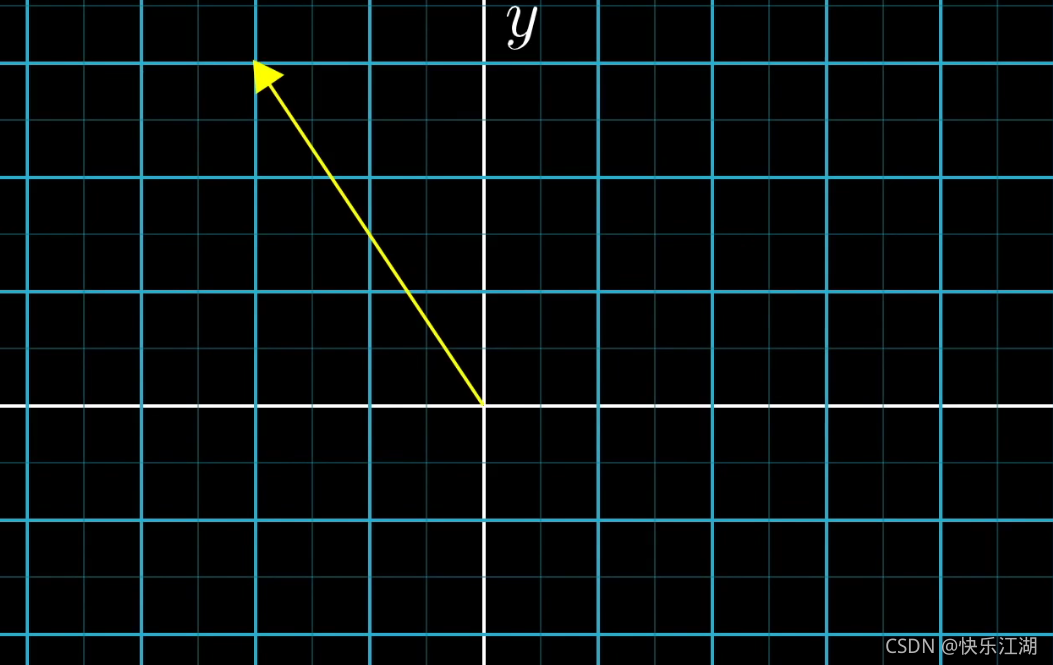
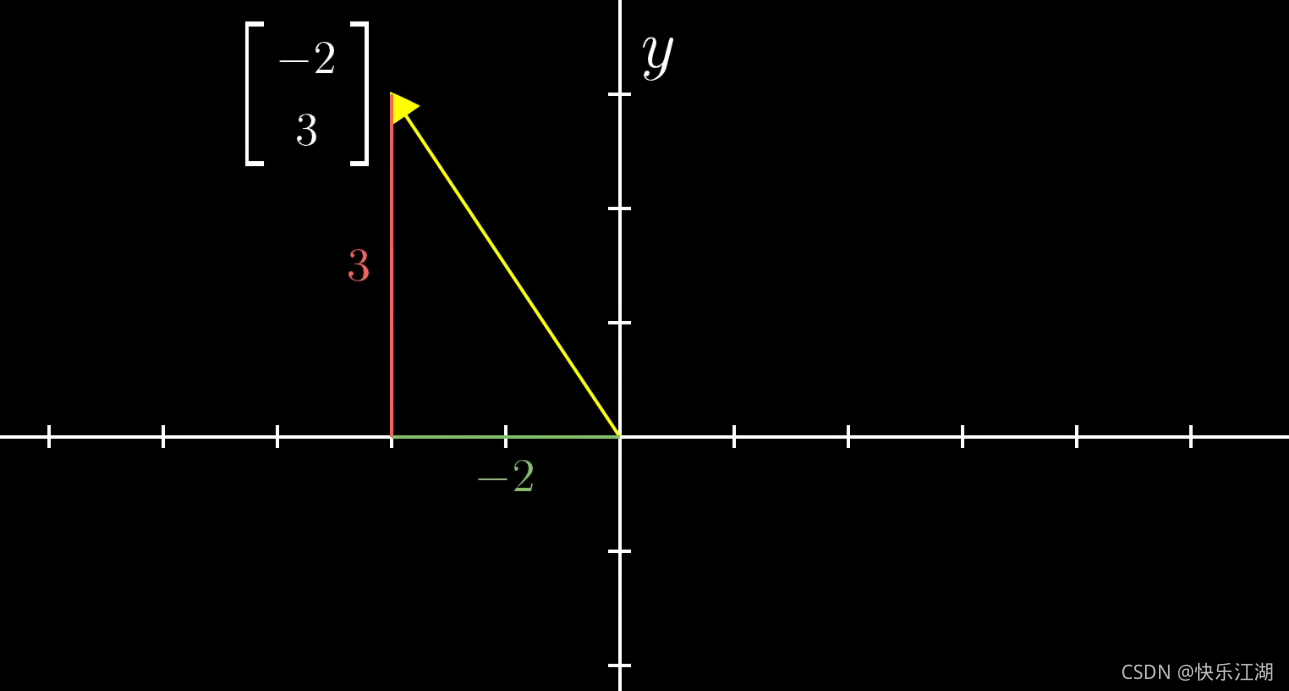
以 ( − 2 3 ) \begin{pmatrix} -2\\ 3\end{pmatrix} (−23)为例,这一对数表示了如何从原点(向量起点)到达末端(向量终点)。每一对数给出了唯一的一个向量,而每一个向量又恰好对应唯一的一对数
- -2:表示从原点开始沿着平行于X轴的负方向移动两个单位
- 3:表示从上一位置开始沿着平行于Y轴的正方向移动两个单位
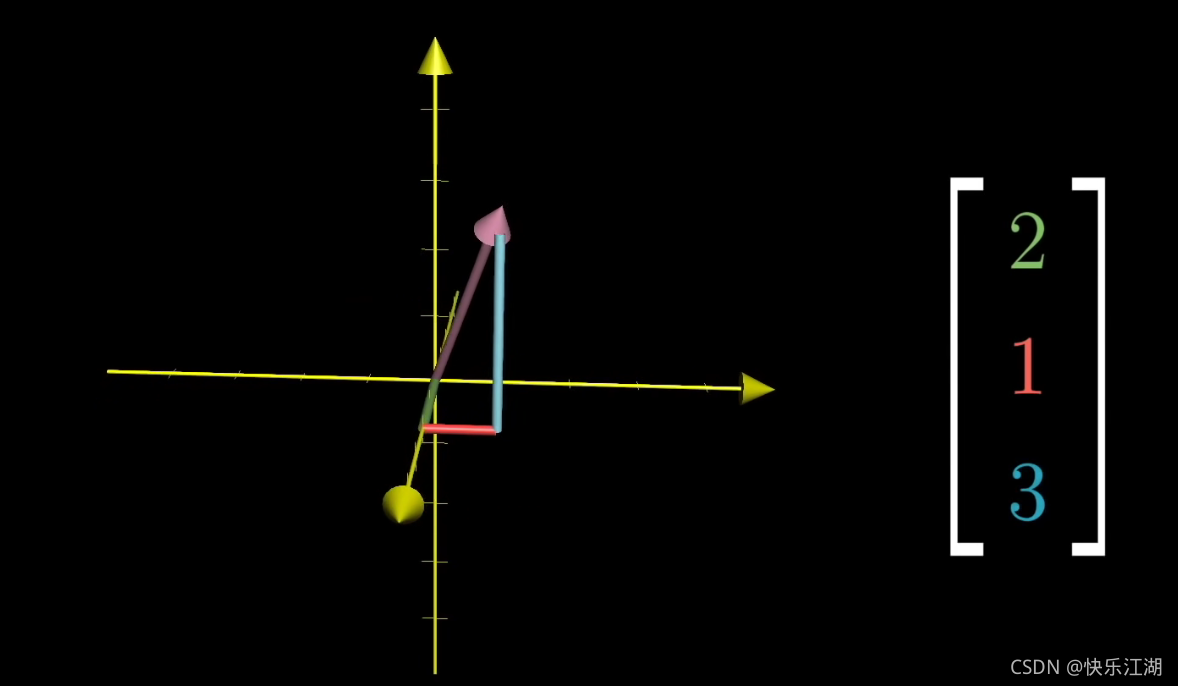
再以 ( 2 1 3 ) \begin{pmatrix} 2\\ 1\\ 3\end{pmatrix} ⎝⎛213⎠⎞为例
- 2:表示从原点开始沿着平行于X轴的正方向移动两个单位
- 1:表示从上一位置开始沿着平行于Y轴的正方向移动一个单位
- 3:表示从上一位置开始沿着平行于Z轴的正方向移动三个单位
二:向量运算
向量运算:即向量之间的运算,在实际问题中会经常涉及向量运算。例如:“在共同申请贷款时,银行会把双方的特征向量作为一个整体来考虑他们是否满足标准”
(1)加减与数乘
加减与数乘:对于给定向量 x 1 = [ g 1 , h 1 , r 1 ] x_{1}=[g_{1}, h_{1}, r_{1}] x1=[g1,h1,r1]和 x 2 = [ g 2 , h 2 , r 2 ] x_{2}=[g_{2}, h_{2}, r_{2}] x2=[g2,h2,r2],则
- 加减: x 1 + x 2 = [ g 1 + g 2 , h 1 + h 2 , r 1 + r 2 ] x_{1}+x_{2}=[g_{1}+g_{2}, h_{1}+h_{2}, r_{1}+r_{2}] x1+x2=[g1+g2,h1+h2,r1+r2]
- 数乘: 2 x 1 = [ 2 g 1 , 2 h 1 , 2 r 1 ] 2x_{1}=[2g_{1}, 2h_{1}, 2r_{1}] 2x1=[2g1,2h1,2r1]
向量加法举例: ( 1 2 ) \begin{pmatrix} 1\\ 2\end{pmatrix} (12)+ ( 3 − 1 ) \begin{pmatrix} 3\\ -1\end{pmatrix} (3−1)= ( 4 1 ) \begin{pmatrix} 4\\ 1\end{pmatrix} (41)
首先 ( 1 2 ) \begin{pmatrix} 1\\ 2\end{pmatrix} (12)和 ( 3 − 1 ) \begin{pmatrix} 3\\ -1\end{pmatrix} (3−1)这两个向量在坐标系中表示如下
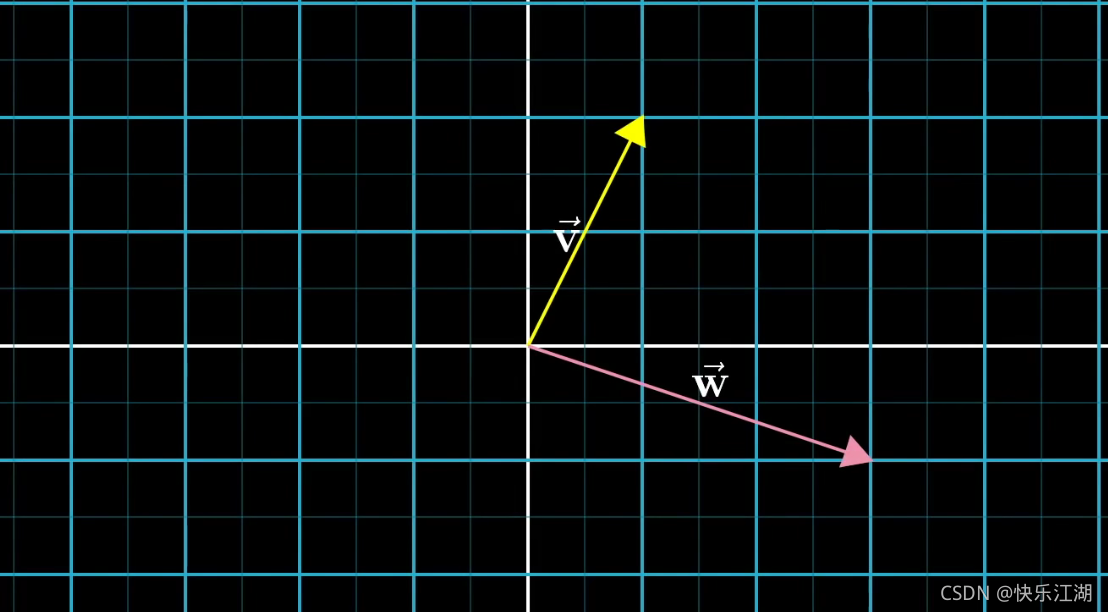
移动第二个向量,使其起点对齐至第一个向量的末尾,然后连线
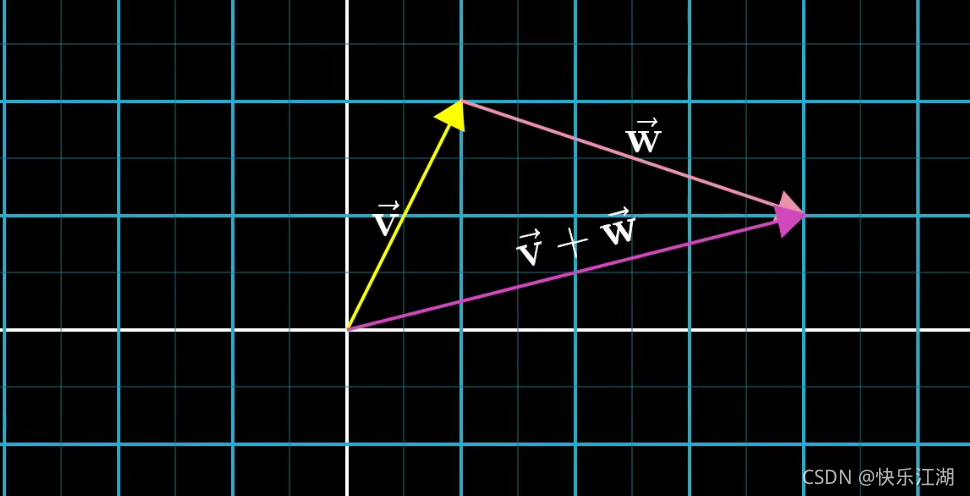
为什么向量加法要这样操作呢?其实向量从某种方面来讲,揭示的是一种运动趋势,自然就有方向和距离,所以大家可以看到向量的和其实就是最终的运动趋势。体现在运算上,就是各个分量对应相加
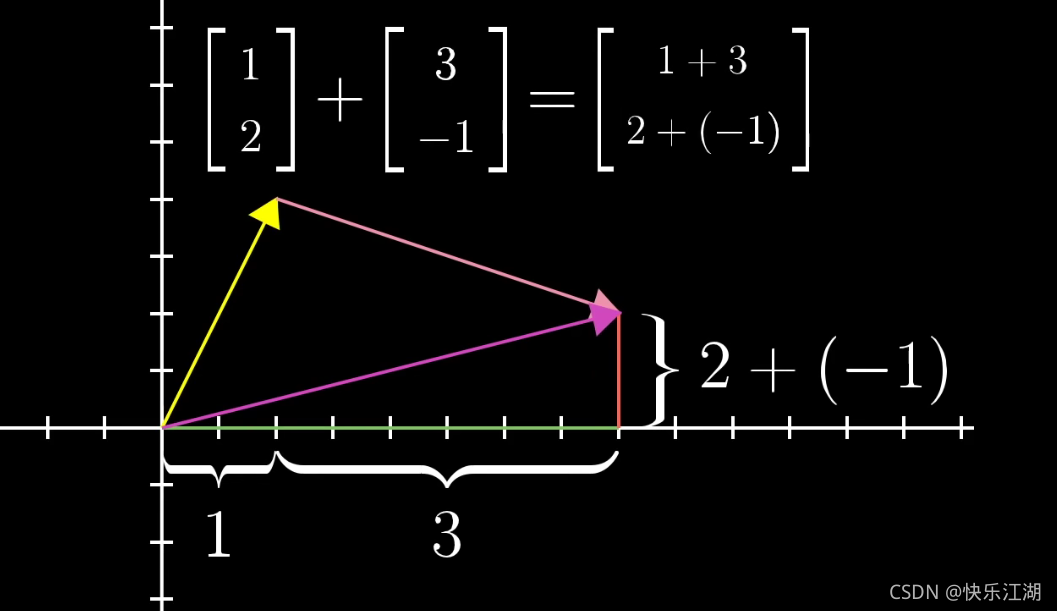
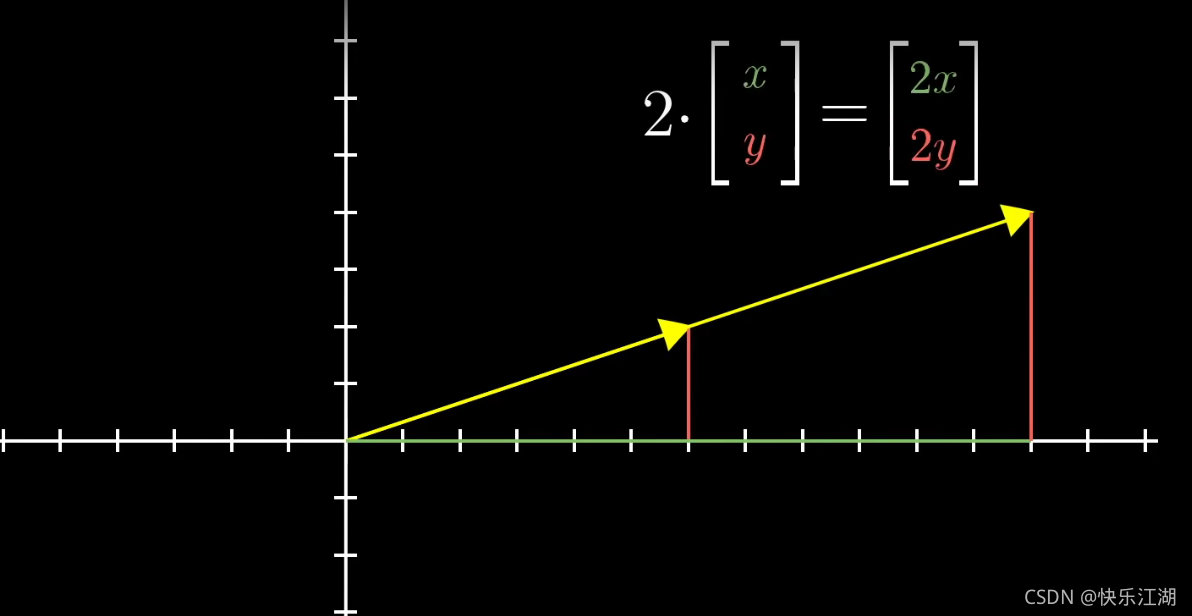
向量数乘举例:2· ( 1 2 ) \begin{pmatrix} 1\\ 2\end{pmatrix} (12)= ( 2 4 ) \begin{pmatrix} 2\\ 4\end{pmatrix} (24)
对于一个向量,对其延长2倍等于把它的每个分量都乘以2,也即
2·
(
1
3
)
\begin{pmatrix} 1\\ 3\end{pmatrix}
(13)=
(
1
×
2
3
×
2
)
\begin{pmatrix} 1×2\\ 3×2\end{pmatrix}
(1×23×2) =
(
2
6
)
\begin{pmatrix} 2\\ 6\end{pmatrix}
(26)
(2)向量内积
A:为什么需要向量内积
在人工智能领域处理数据时,常常会构造一个特征空间 [ g , h , r ] [g, h, r] [g,h,r]然后把所有数据都变换到空间中去,然后通过操控特征空间对数据做出评判和处理
如果这个空间只有一个维度,那么在坐标轴上就是一条直线,例如 x = 10 x=10 x=10,其右侧大于 0 0 0,左侧小于 0 0 0
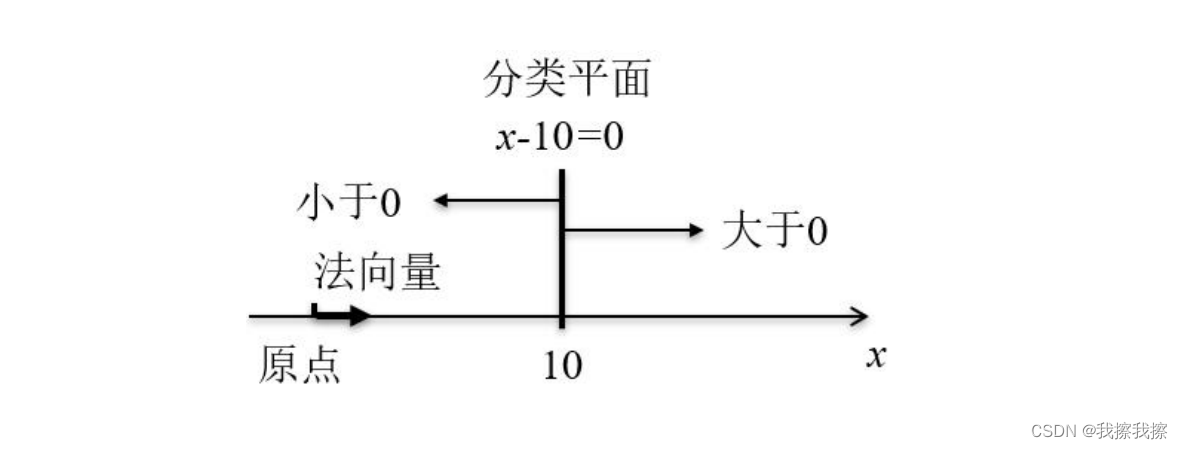
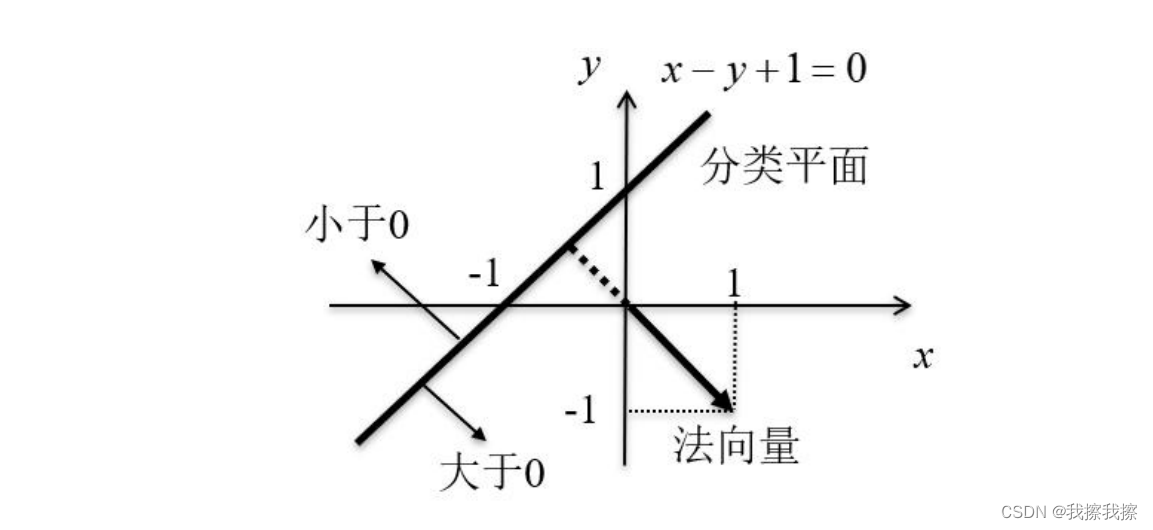
如果这个空间有两个维度,那么就是一个平面,以直线方程 x − y + 1 = 0 x-y+1=0 x−y+1=0,在法向量那一侧的大于0,与法向量相反的那一侧小于0。同时 x − y + 1 = 0 x-y+1=0 x−y+1=0实际上就是向量 a = [ x , y , 1 ] a=[x, y, 1] a=[x,y,1]和向量 w = [ 1 , − 1 , 1 ] w=[1,-1,1] w=[1,−1,1]的内积,也即 w a T = 0 wa^{T}=0 waT=0
B:向量内积
向量内积:给定向量 x 1 = [ x 1 , 1 , x 1 , 2 , . . . , x 1 , d ] x_{1}=[x_{1,1},x_{1,2},...,x_{1,d}] x1=[x1,1,x1,2,...,x1,d]和向量 x 2 = [ x 2 , 1 , x 2 , 2 , . . . , x 2 , d ] x_{2}=[x_{2,1},x_{2,2},...,x_{2,d}] x2=[x2,1,x2,2,...,x2,d],则 x 1 x_{1} x1和 x 2 x_{2} x2的内积为 x 1 x 2 T = < x 1 , x 2 > = ∑ i = 1 d x 1 , i x 2 , i x_{1}x_{2}^{T}=<x_{1},x_{2}>=\sum\limits_{i=1}^{d}x_{1,i}x_{2,i} x1x2T=<x1,x2>=i=1∑dx1,ix2,i,向量内积满足交换律,即 < x 1 , x 2 > = < x 2 , x 1 > <x_{1},x_{2}>=<x_{2},x_{1}> <x1,x2>=<x2,x1>。向量进行内积运算的结果为标量,这意味着内积的转置等于自身,即 x 1 x 2 T = x 2 x 1 T = ( x 1 x 2 T ) T x_{1}x_{2}^{T}=x_{2}x_{1}^{T}=(x_{1}x_{2}^{T})^{T} x1x2T=x2x1T=(x1x2T)T
向量内积的几何意义有两点, < x 1 , x 2 > = ∣ ∣ x 1 ∣ ∣ ∣ ∣ x 2 ∣ ∣ c o s θ <x_{1},x_{2}>=||x_{1}|| ||x_{2}||cos\theta <x1,x2>=∣∣x1∣∣∣∣x2∣∣cosθ
- 表征或计算两个向量之间的夹角
- 向量 x 2 x_{2} x2在向量 x 1 x_{1} x1方向上的投影
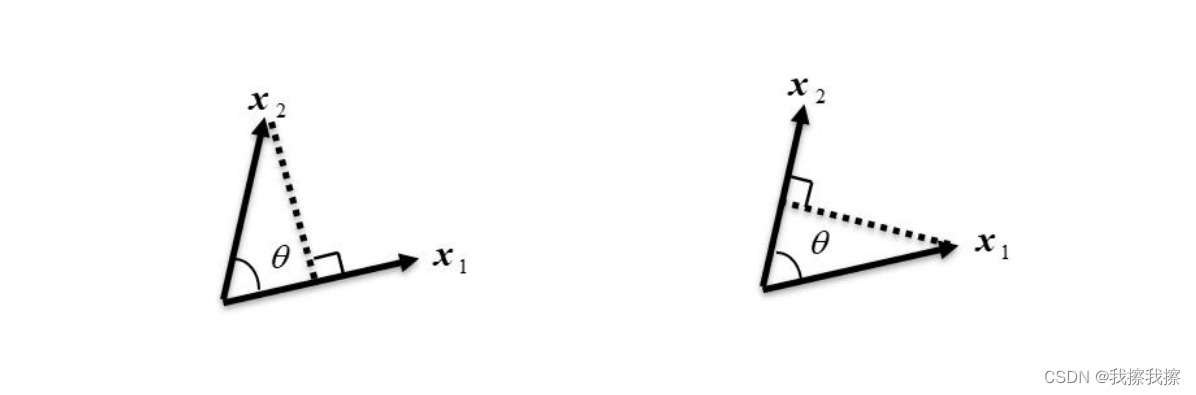
如果向量内积结果为0,这表明两个向量正交;如果相互正交的两个向量均为单位向量,则称这种正交为标准正交
C:柯西-施瓦茨不等式
柯西-施瓦茨不等式:由于 c o s θ ∈ [ − 1 , 1 ] cos\theta \in[-1,1] cosθ∈[−1,1],所以可得柯西-施瓦茨不等式
− ∣ ∣ x 1 ∣ ∣ ∣ ∣ x 2 ∣ ∣ ≤ < x 1 , x 2 > ≤ ∣ ∣ x 1 ∣ ∣ ∣ ∣ x 2 ∣ ∣ -||x_{1}||||x_{2}||\leq <x_{1},x_{2}>\leq ||x_{1}||||x_{2}|| −∣∣x1∣∣∣∣x2∣∣≤<x1,x2>≤∣∣x1∣∣∣∣x2∣∣
所以 θ \theta θ取值不同时,两个向量会呈现出不同的形式
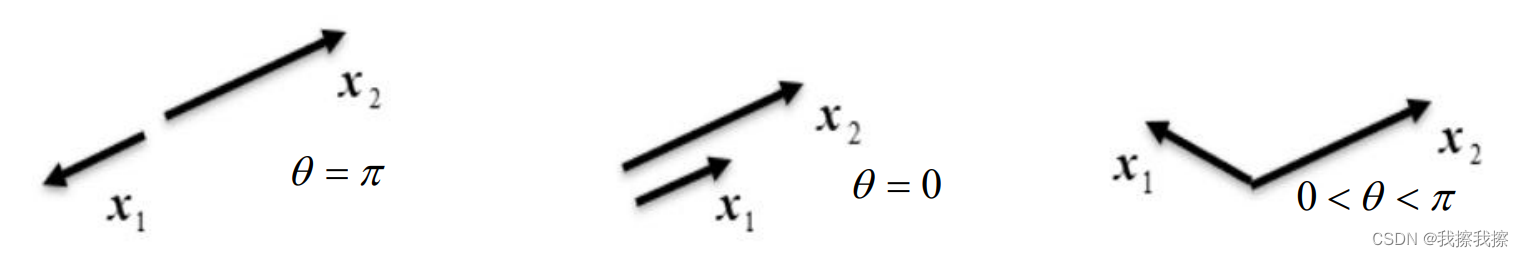
如果两个内积向量均已被单位化(也即长度均为1),则向量内积可以作为两个向量相似程度的判断依据。在长度确定的情况下,内积结果越接近长度的乘积,则向量在方向上越相似

(3)线性组合
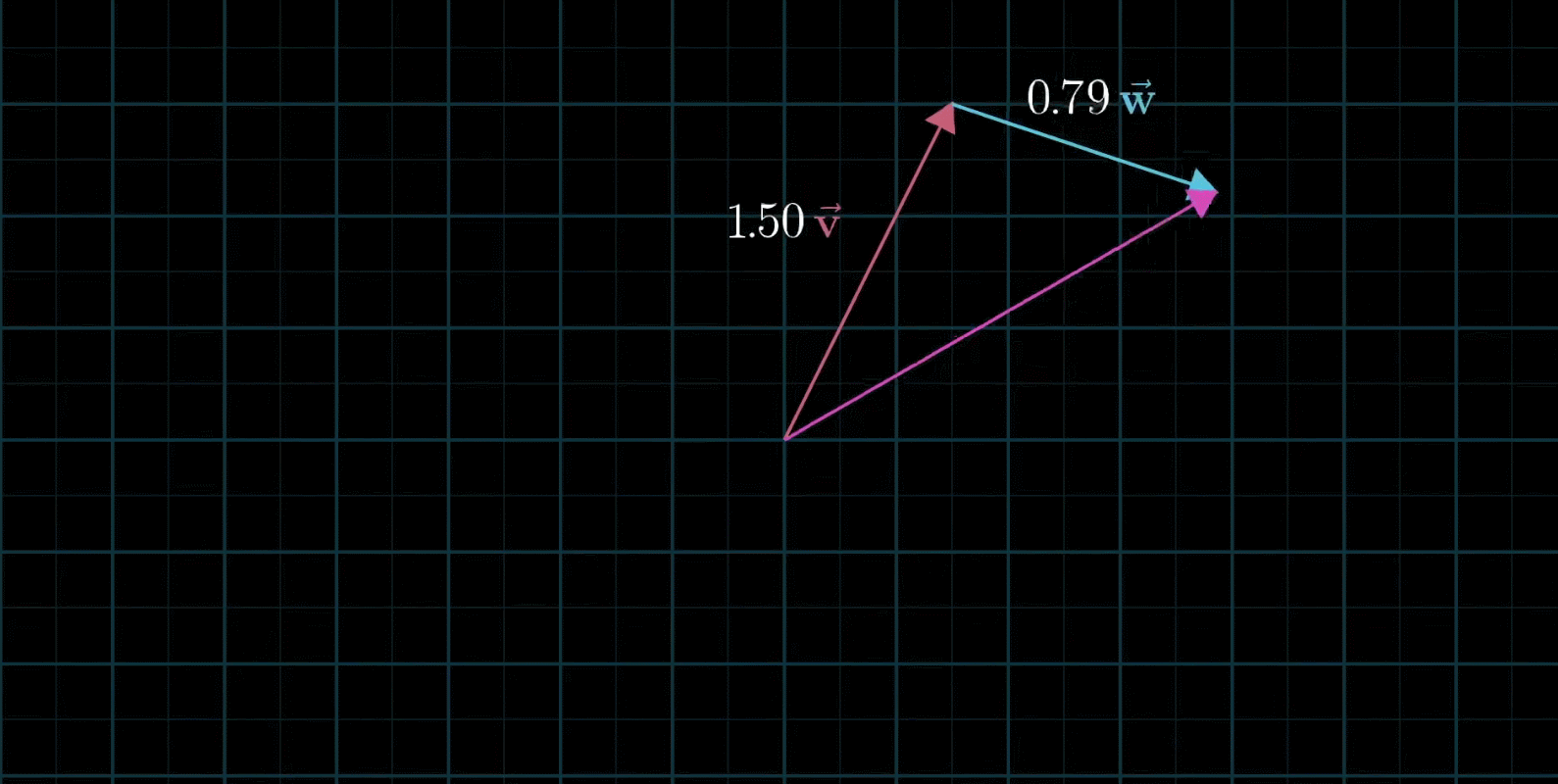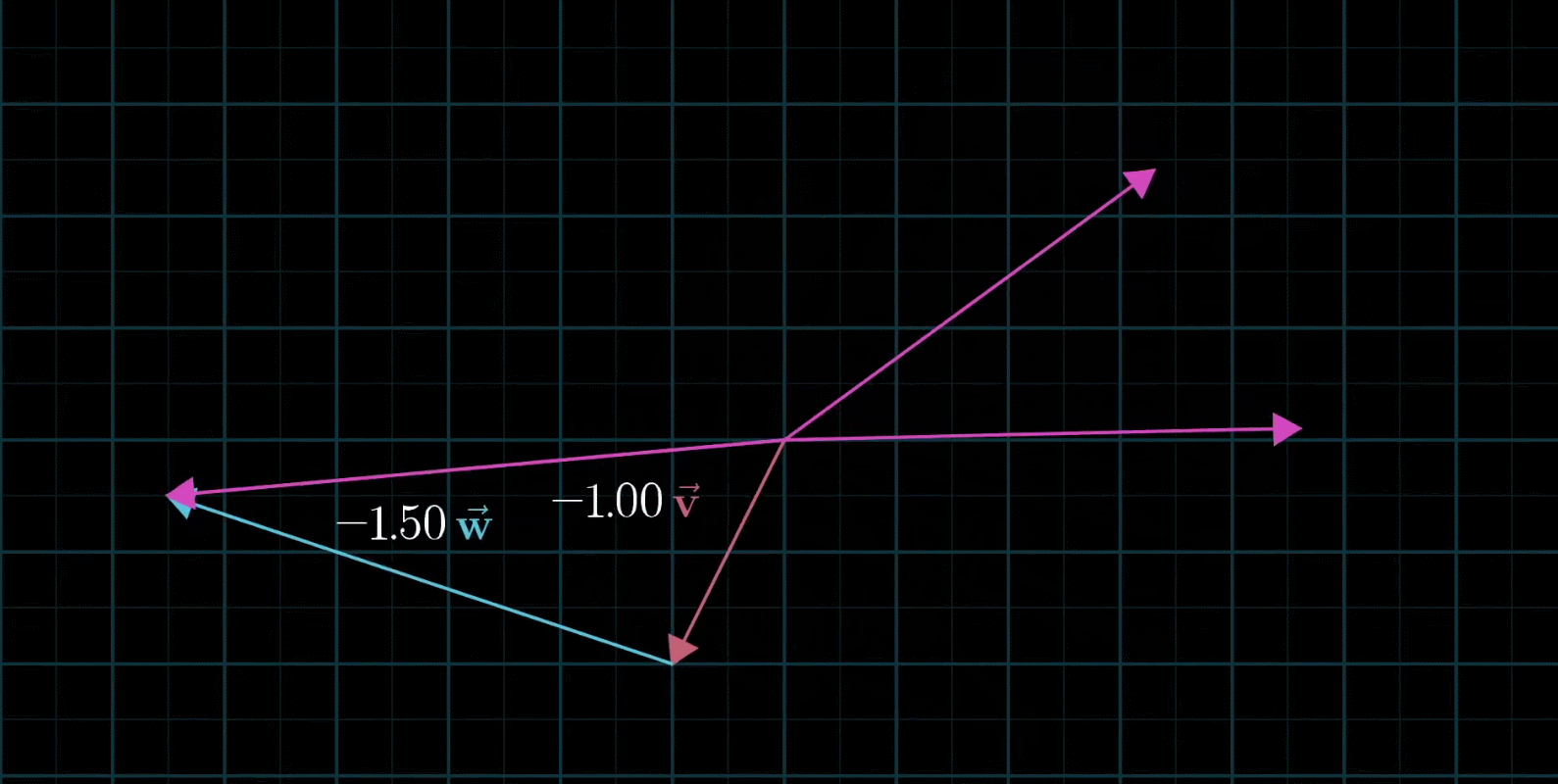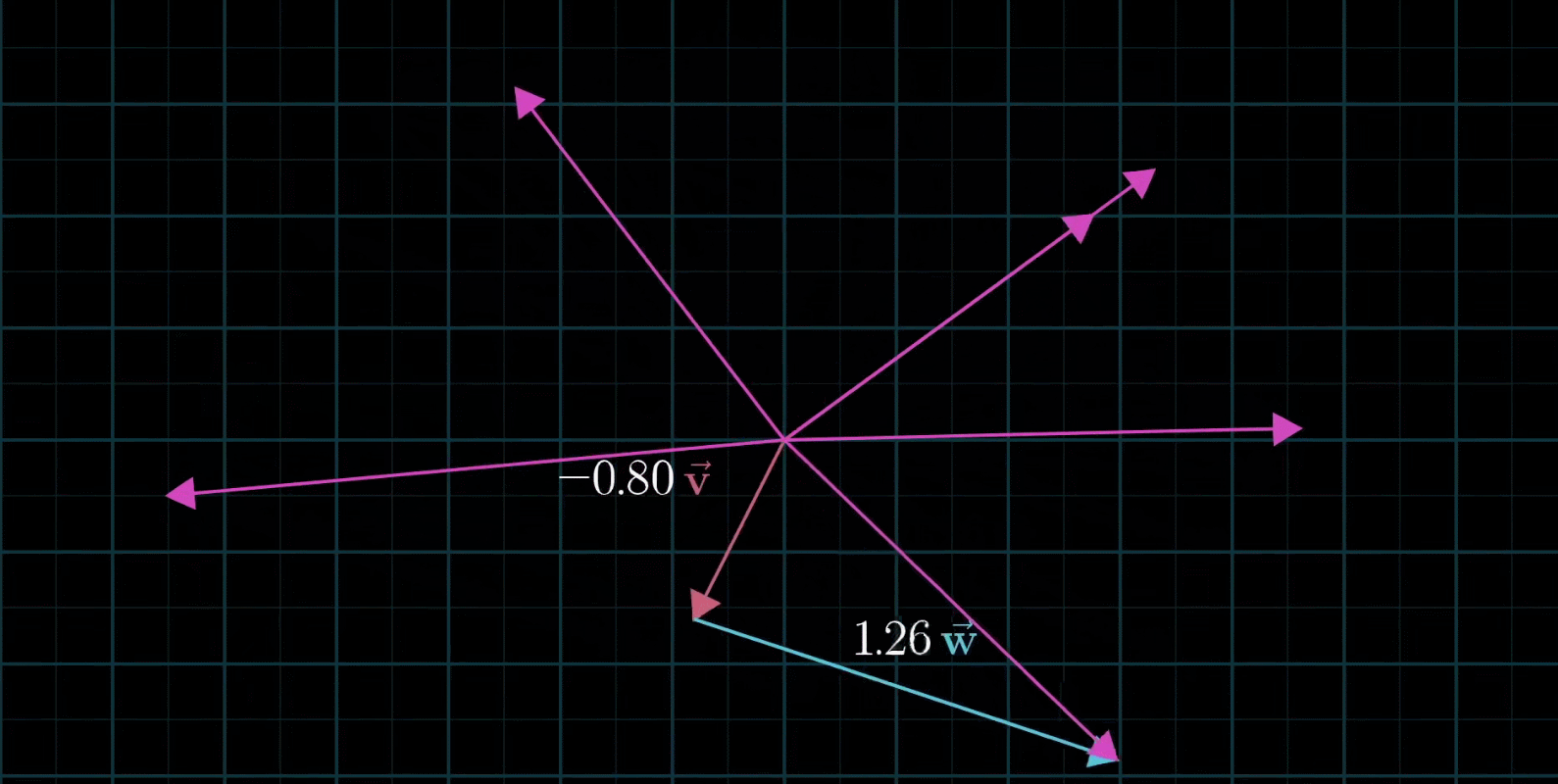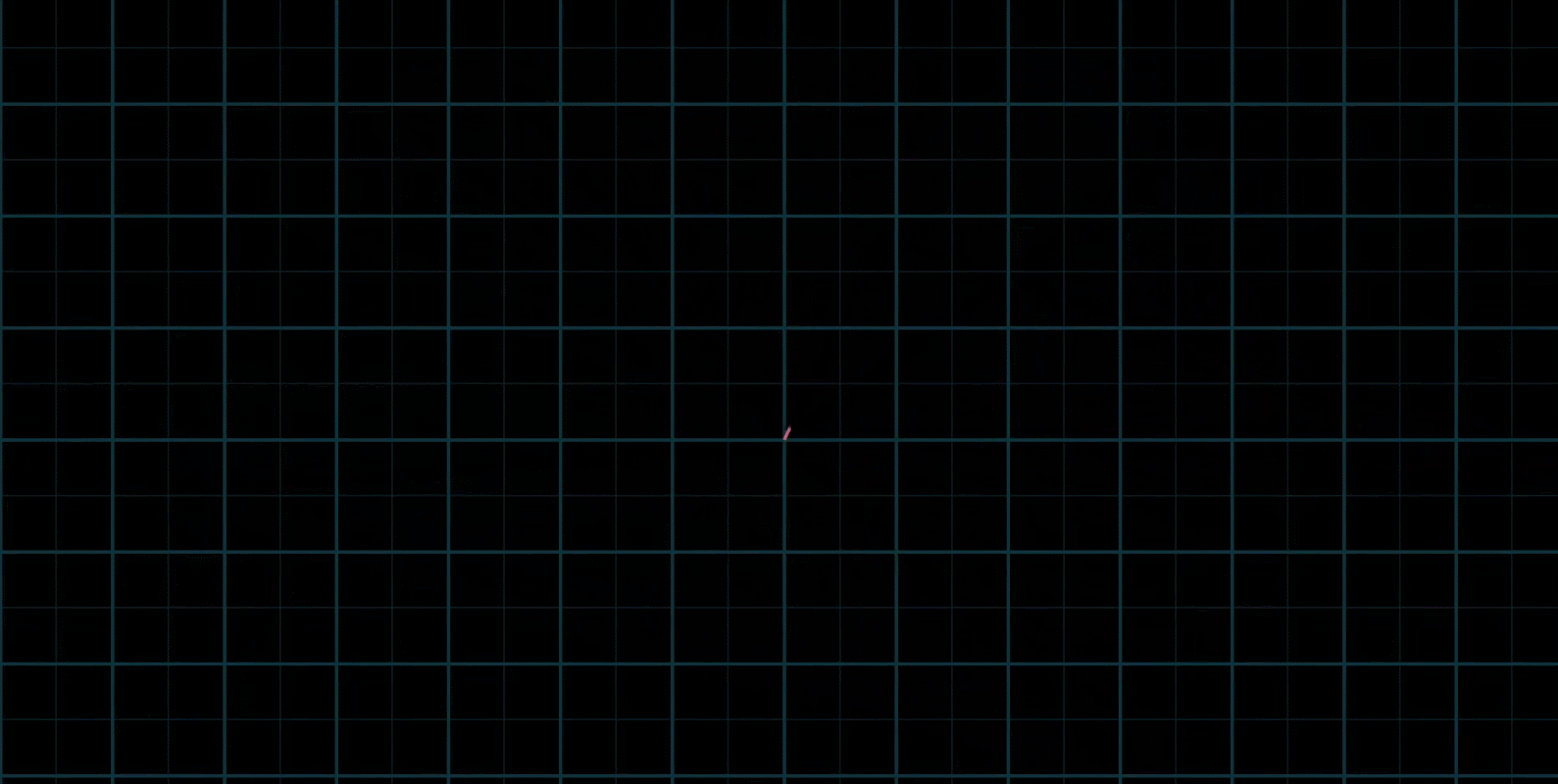
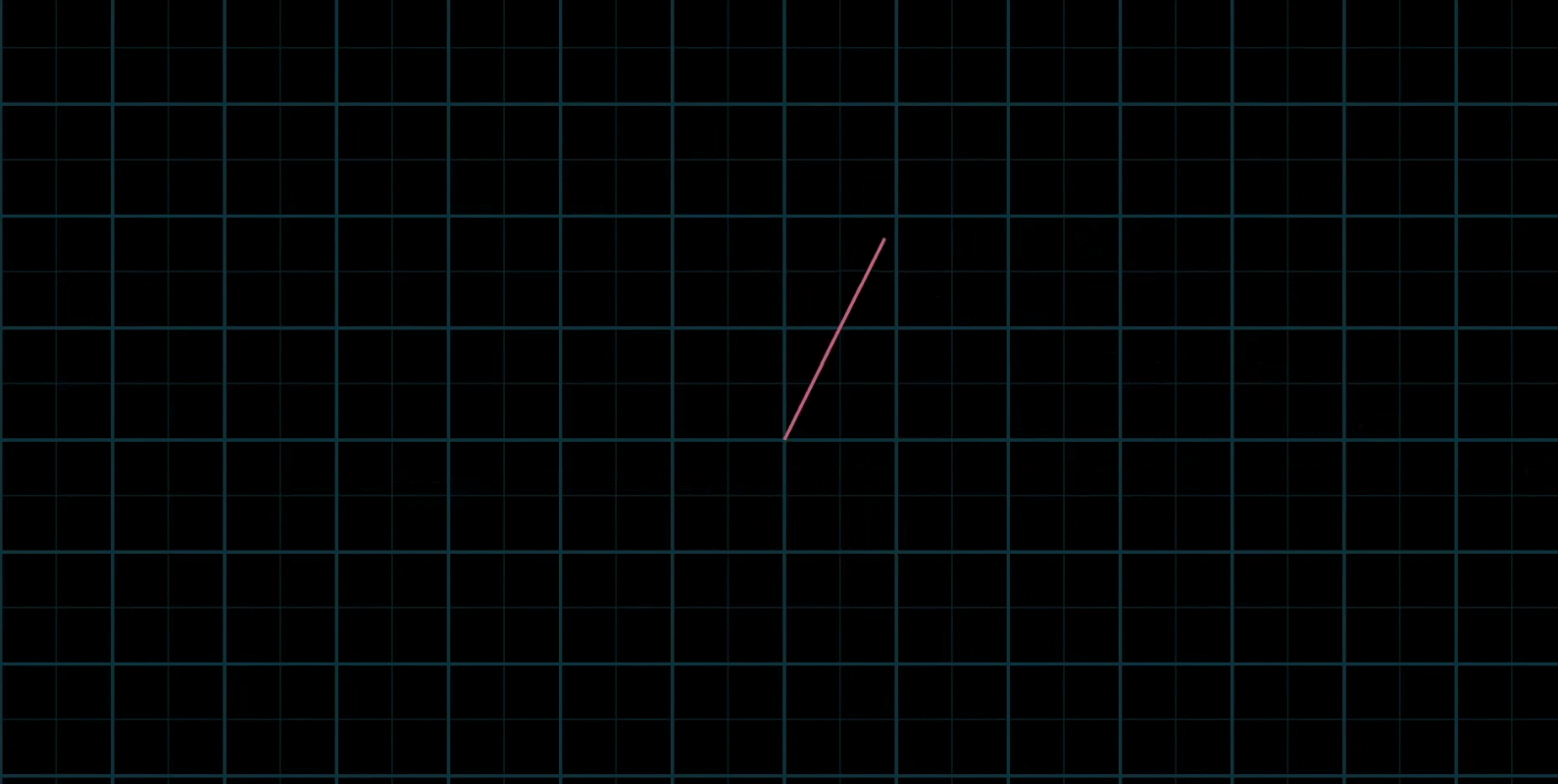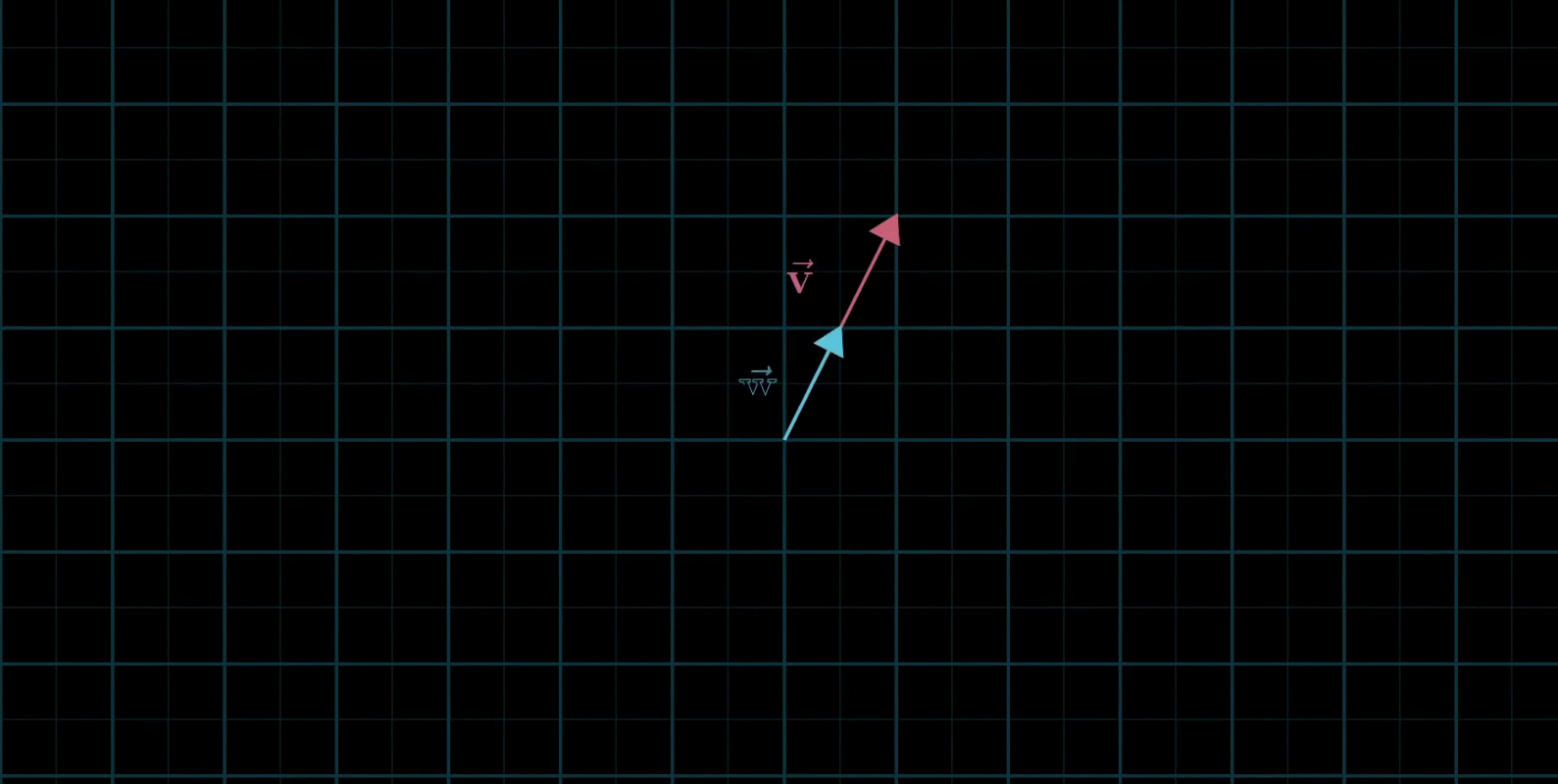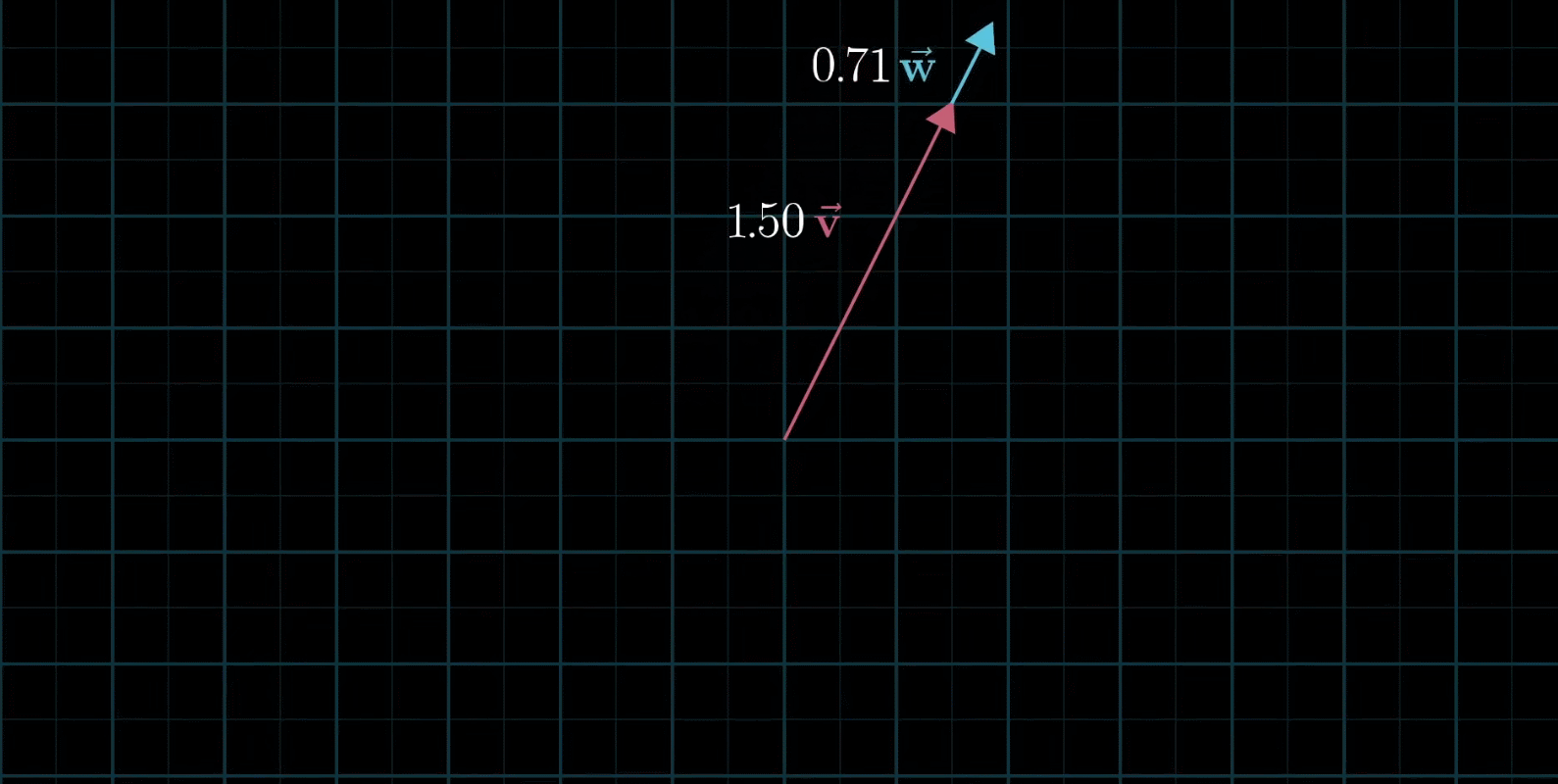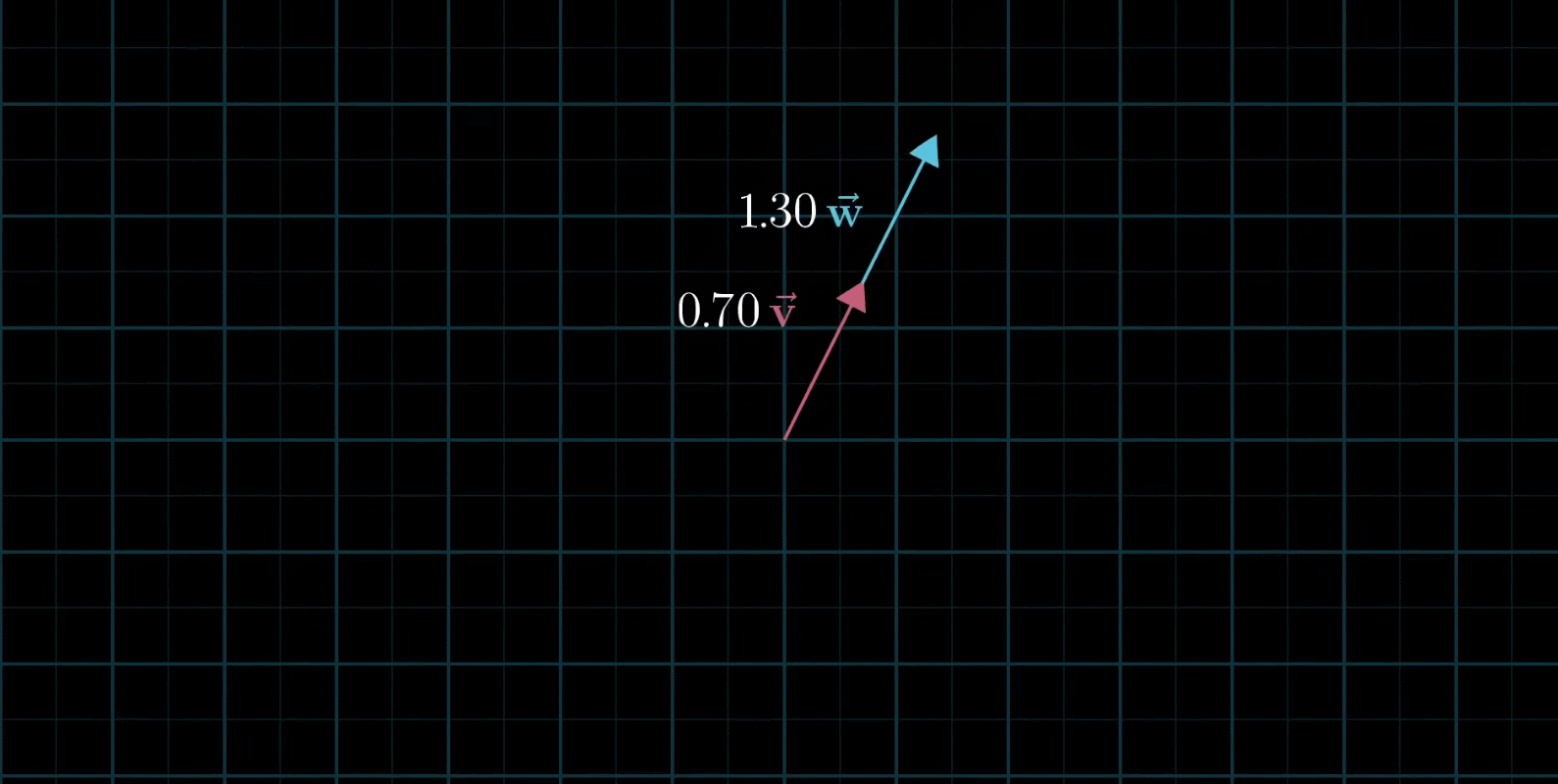
线性组合:两个数乘向量的和称为这两个向量的线性组合
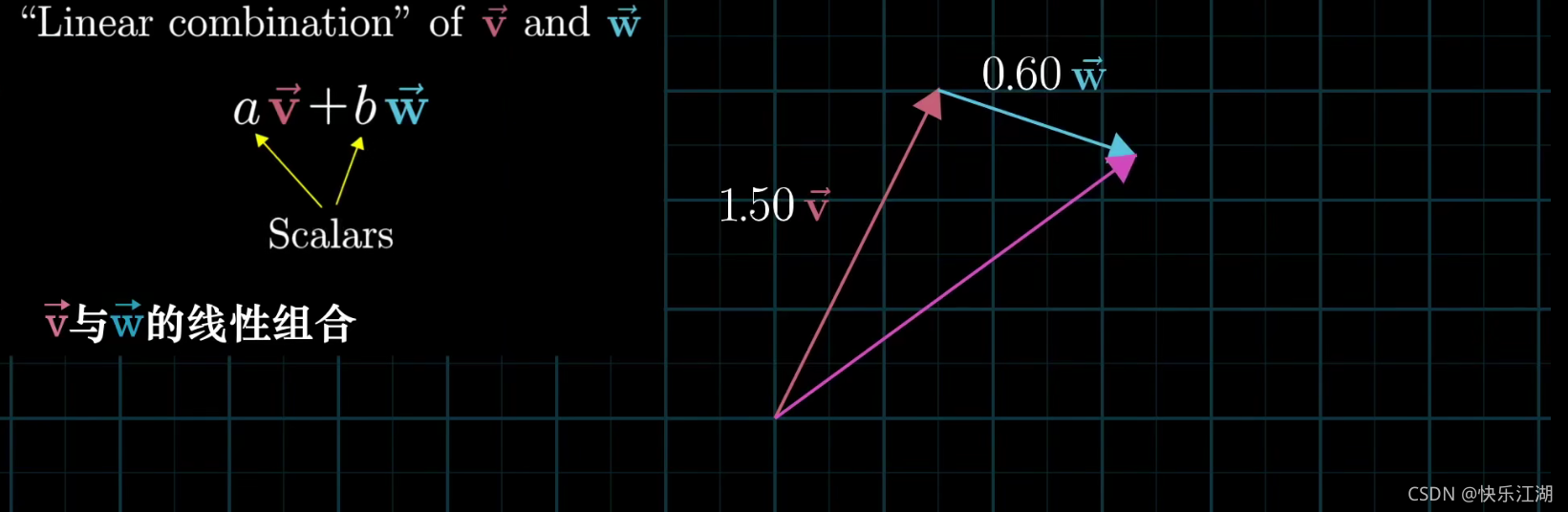

如果固定其中一个标量,让另外一个标量自由变换,那么所能表示的向量的终点会绘成一条直线
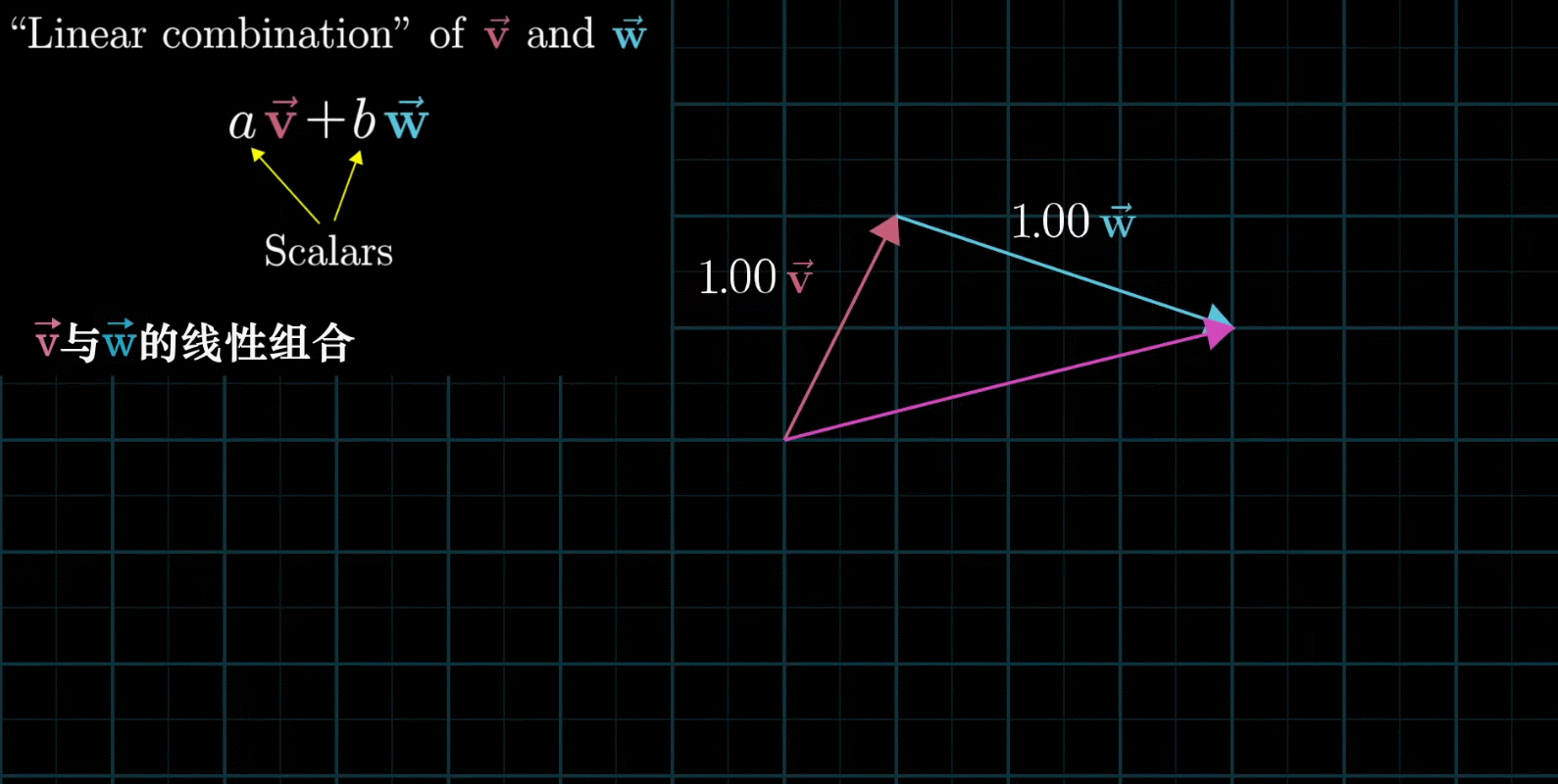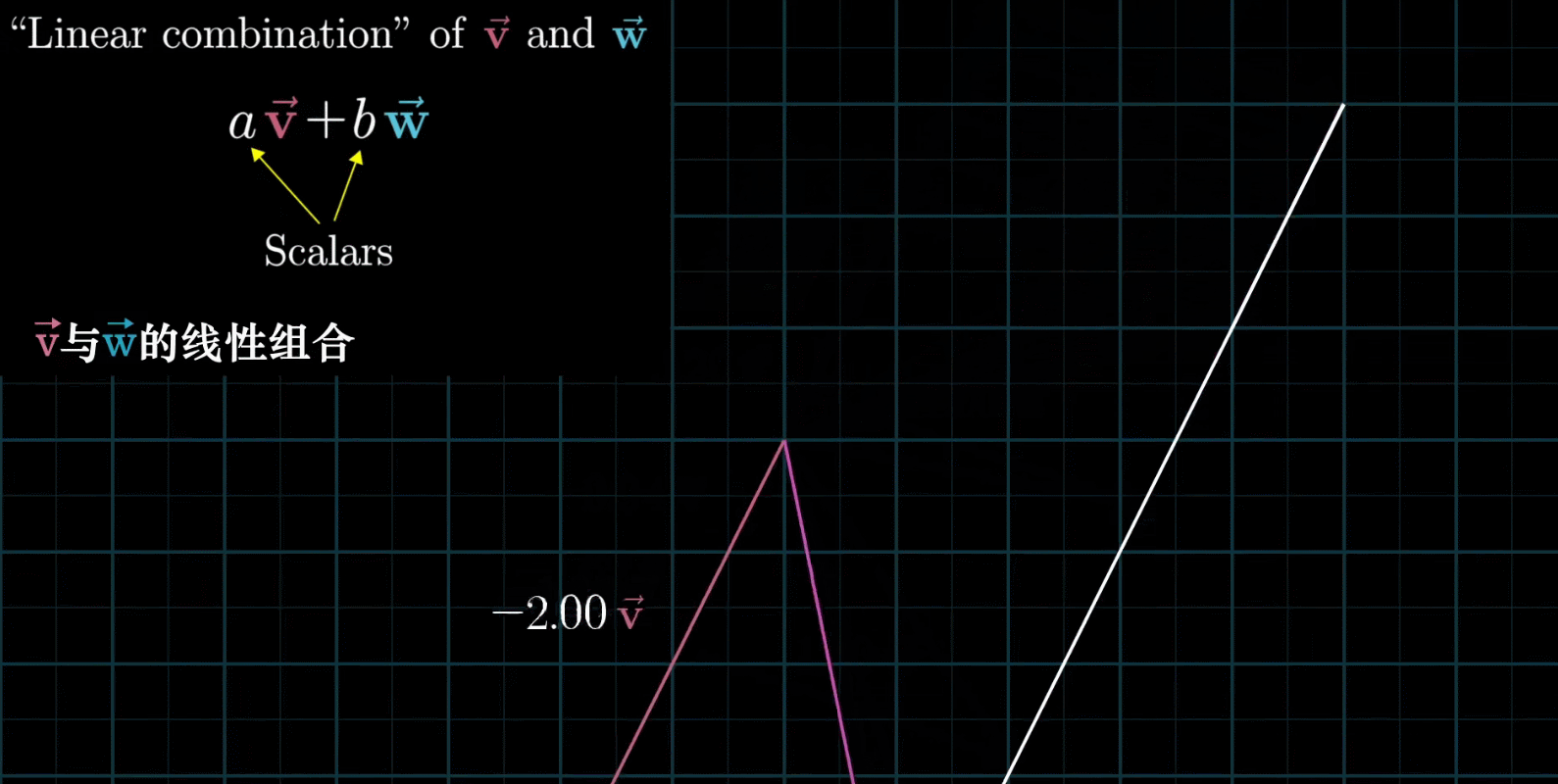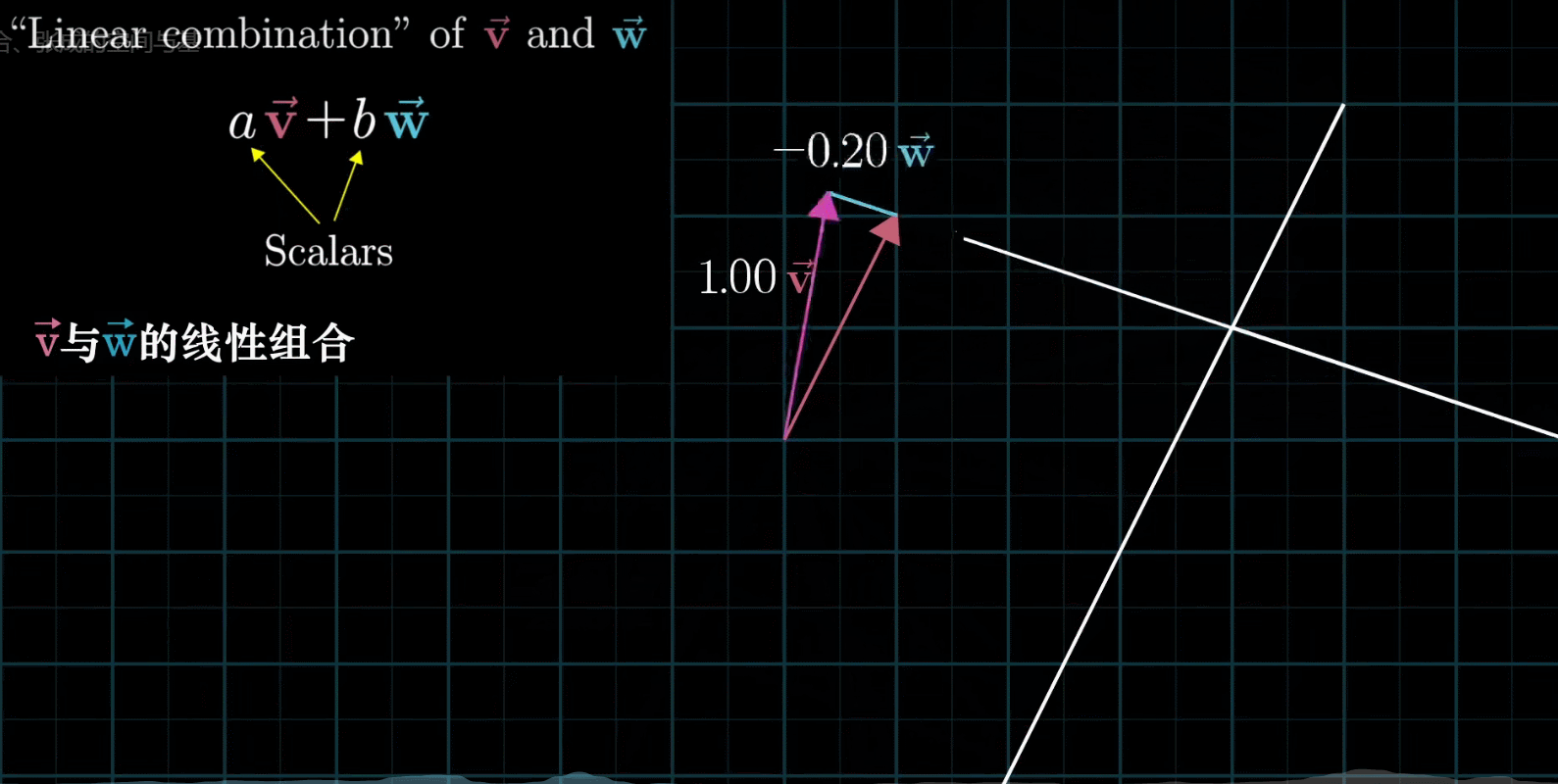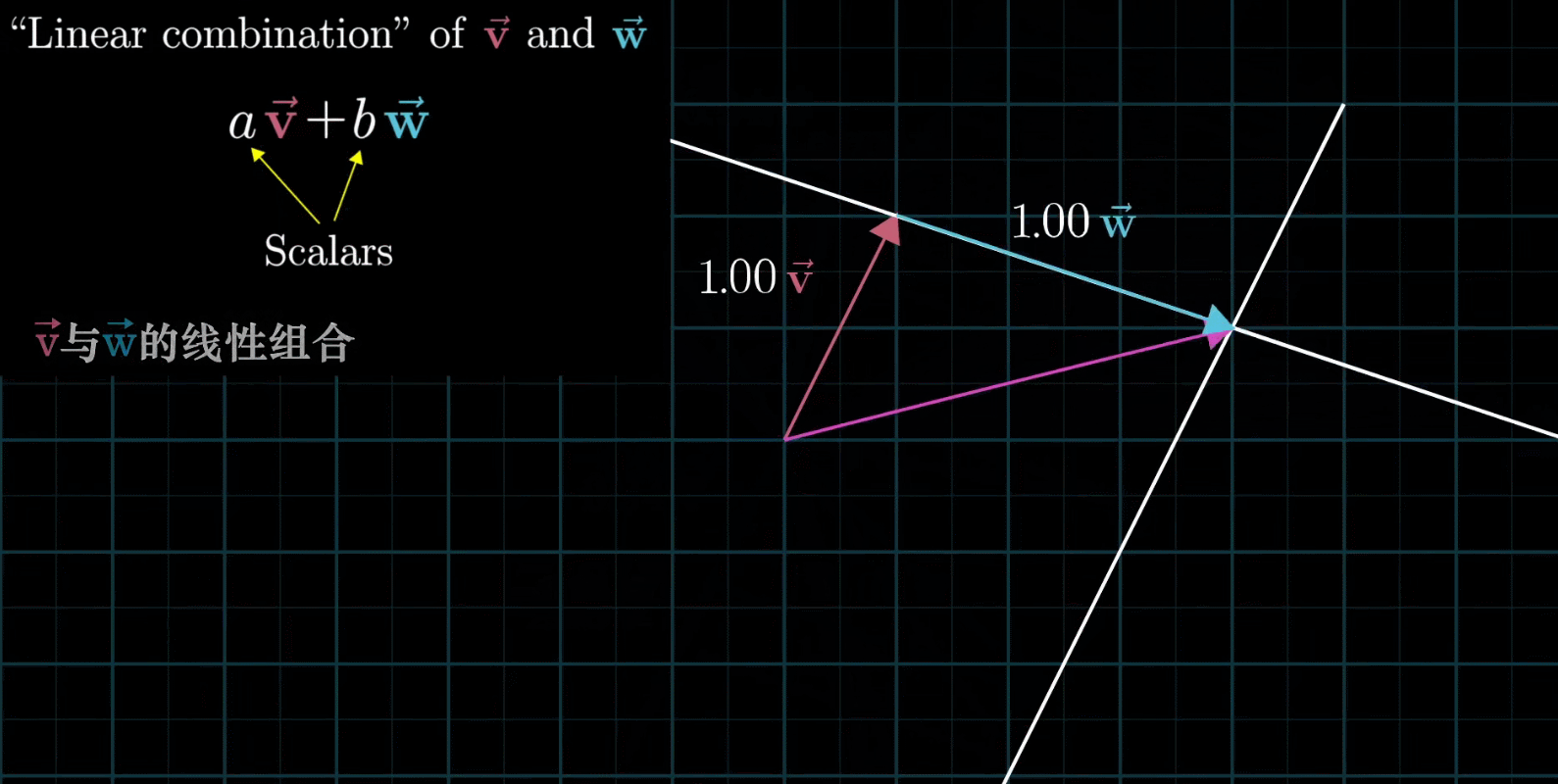
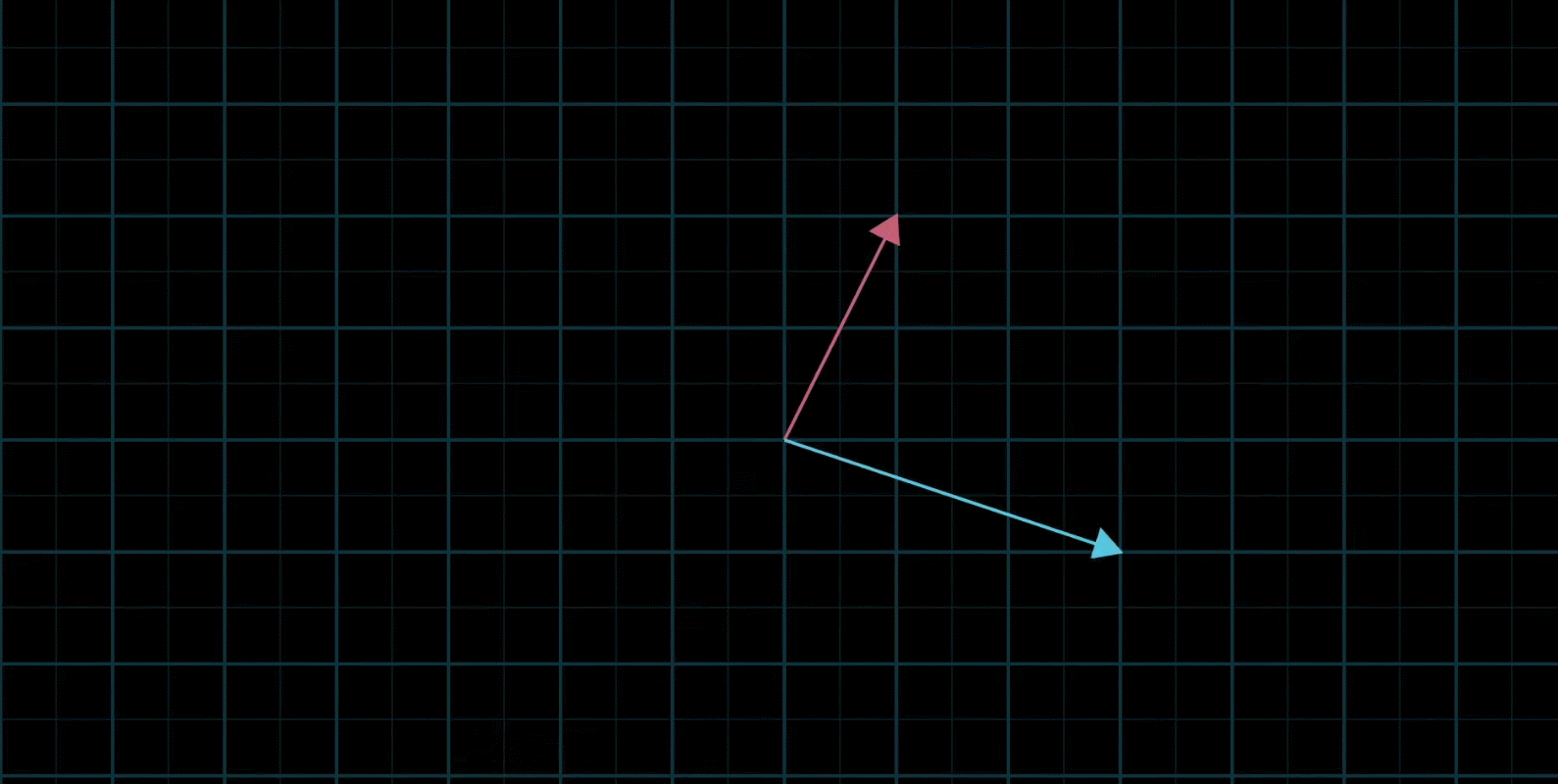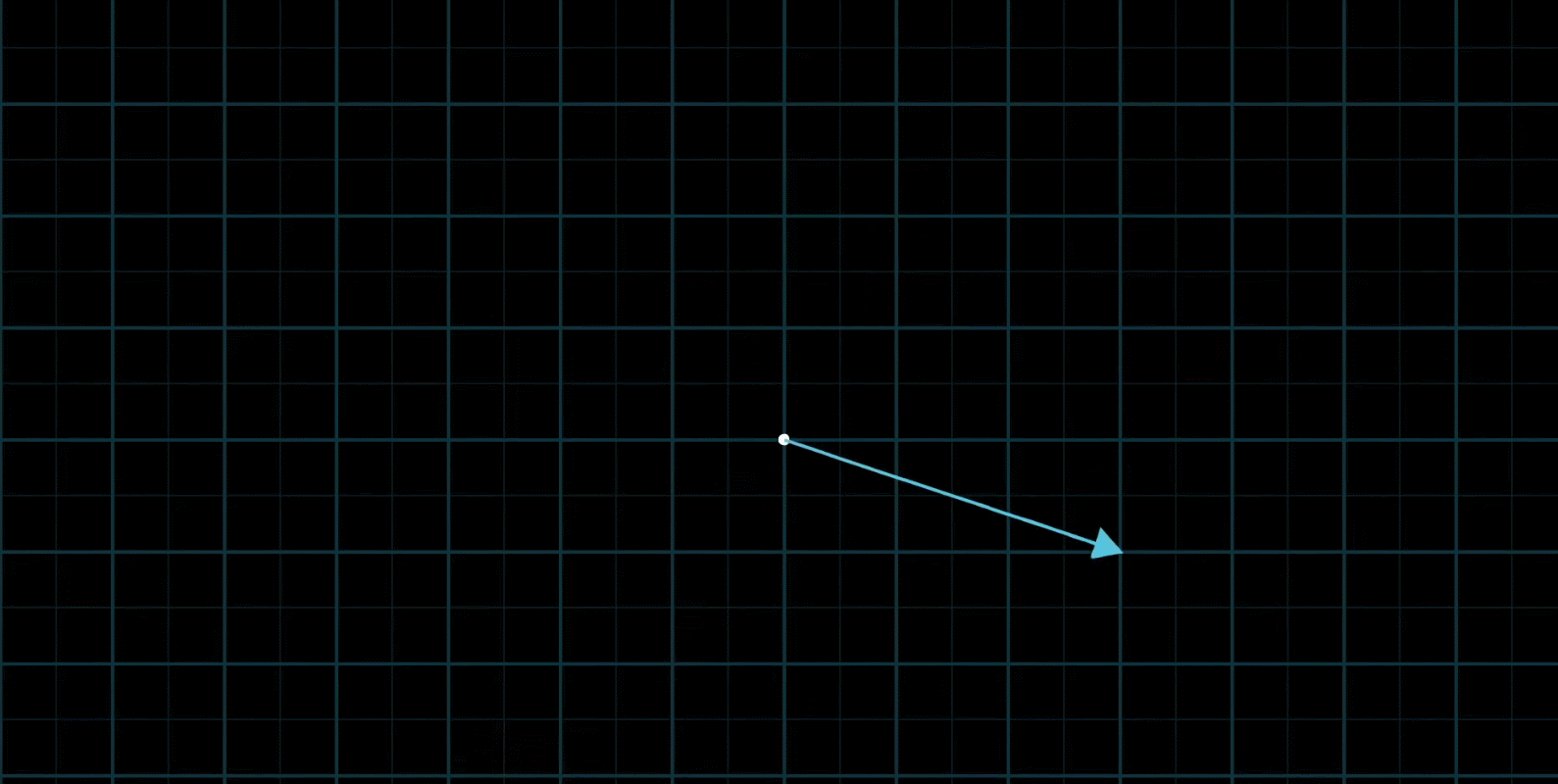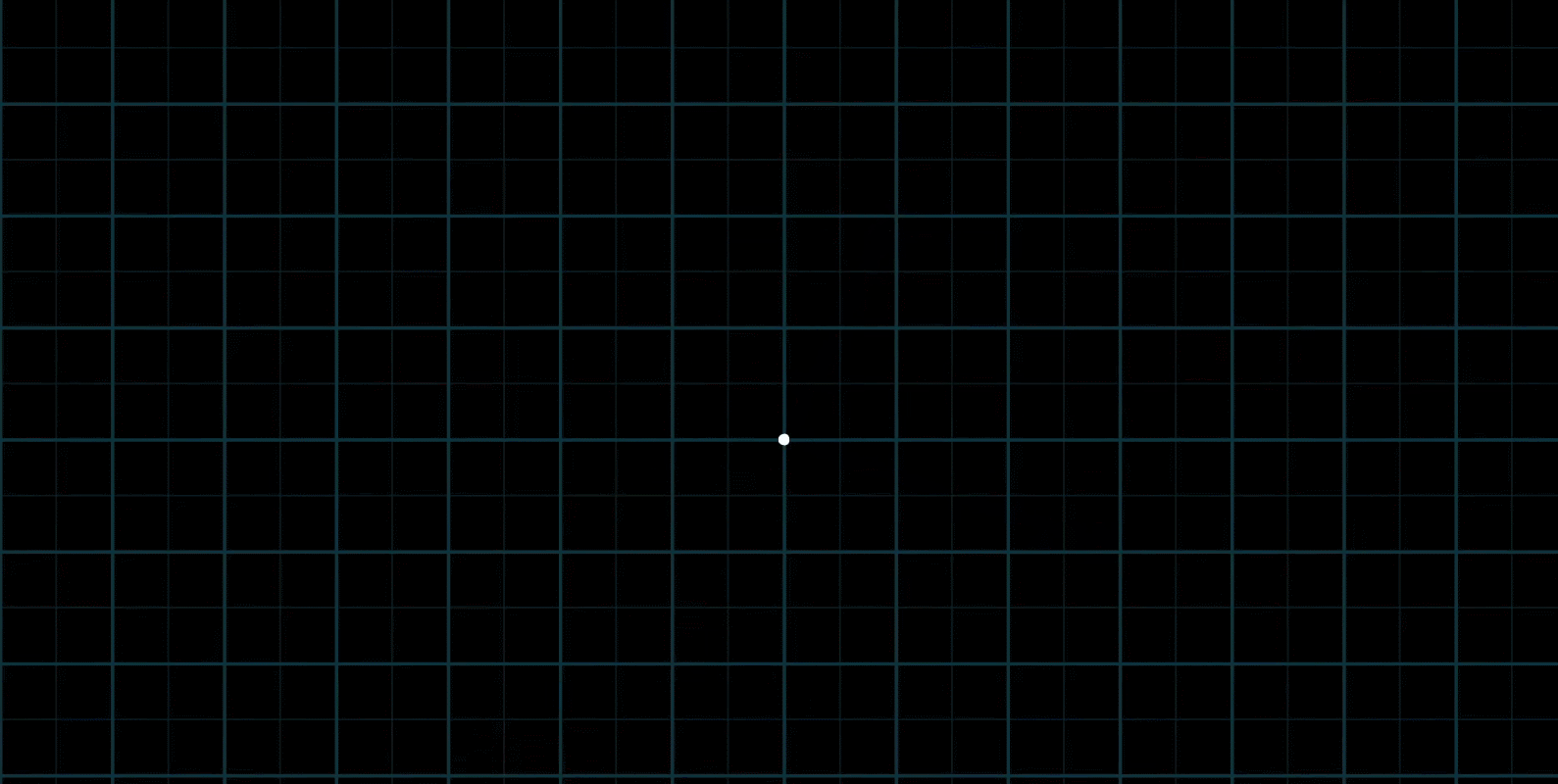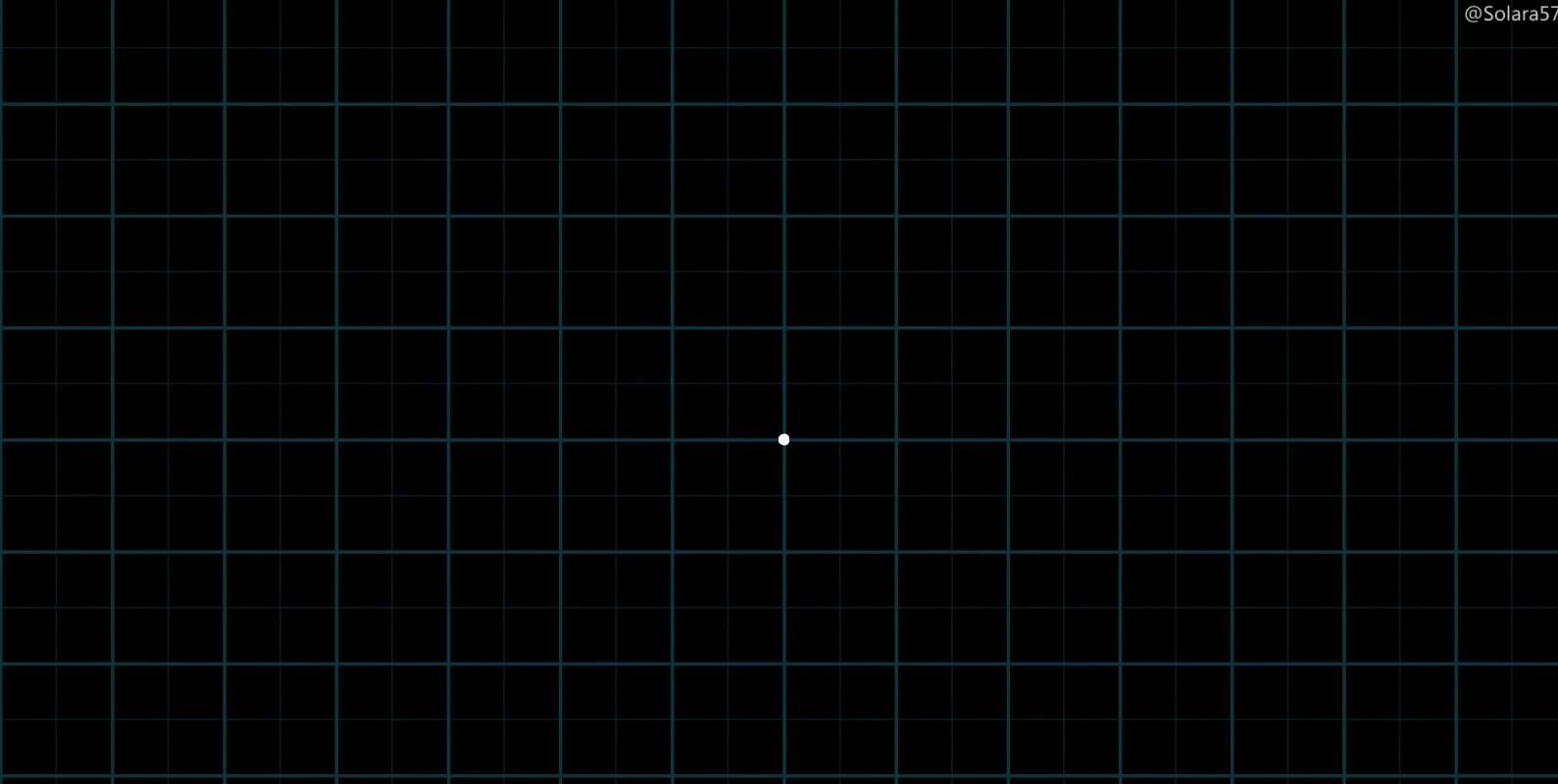
如果让两个标量都自由变换,那么会有以下几种情况:
-
在大多数情况下,对于一切初始向量,你能到达平面中任何一个点,所有二维向量尽在你的掌握之中
-
有时也会出现两个初始向量共线,那么所产生的新的向量的重点会被限制在一条过原点的直线上
-
还有,两个向量可能都是零向量,那么就只能呆在原地了
三:基向量和向量空间(线性空间)
(1)基向量
基向量:在二维平面直角坐标系中有一对非常特殊的向量
- i i i:指向 x x x轴正方向的单位向量
- j j j:指向 y y y轴正方向的单位向量
以 ( 3 − 2 ) \begin{pmatrix} 3\\ -2\end{pmatrix} (3−2)为例,可以看做是由单向向量 i i i正向拉长为原来的3倍,同时把单位向量 j j j反向拉长为原来的2倍得到
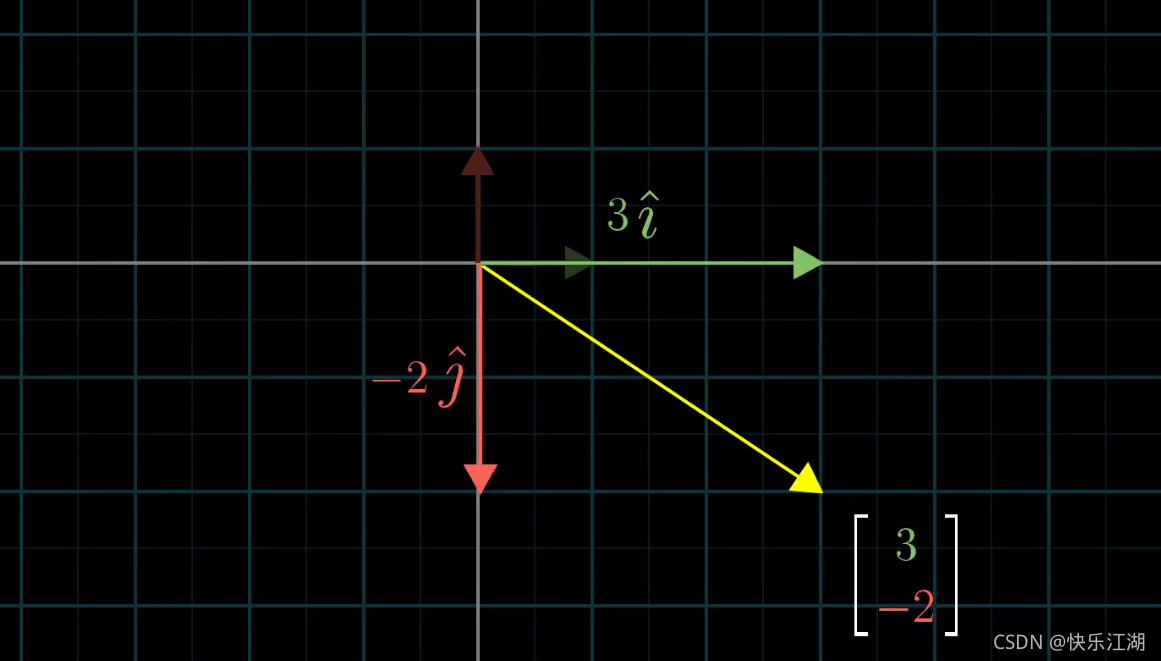
从这个角度上理解这个向量实际上是两个经过缩放的向量的和(注意这个概念非常重要)
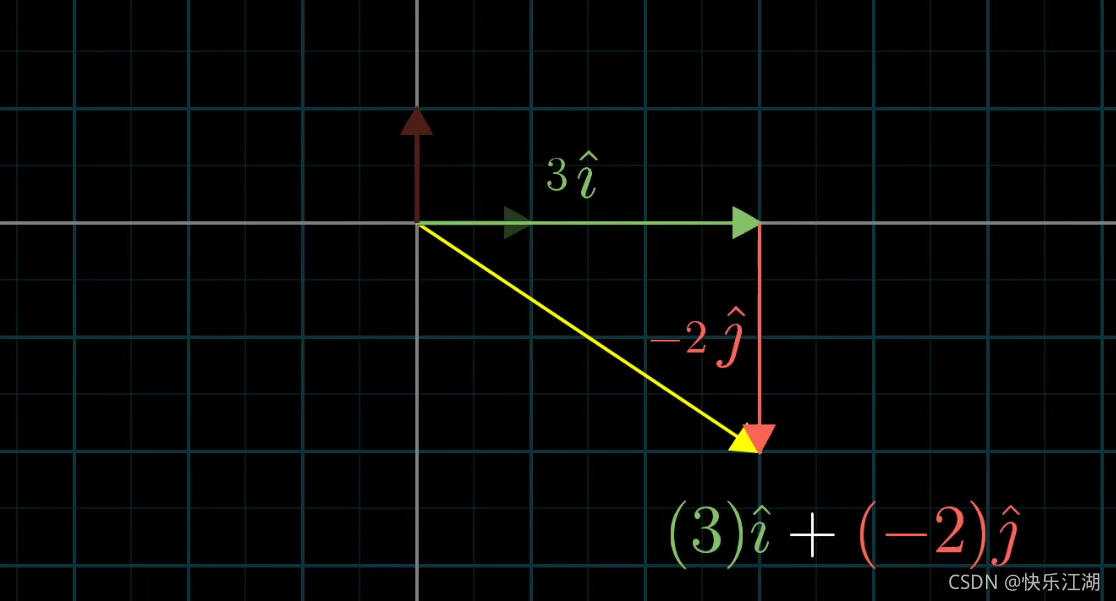
因此,这里我们把 i i i和 j j j称为 x y xy xy坐标系的“基向量”

(2)向量张成的空间
向量张成的空间:它是一个集合,这个集合表示了所有可以由给定向量通过线性组合表示的向量
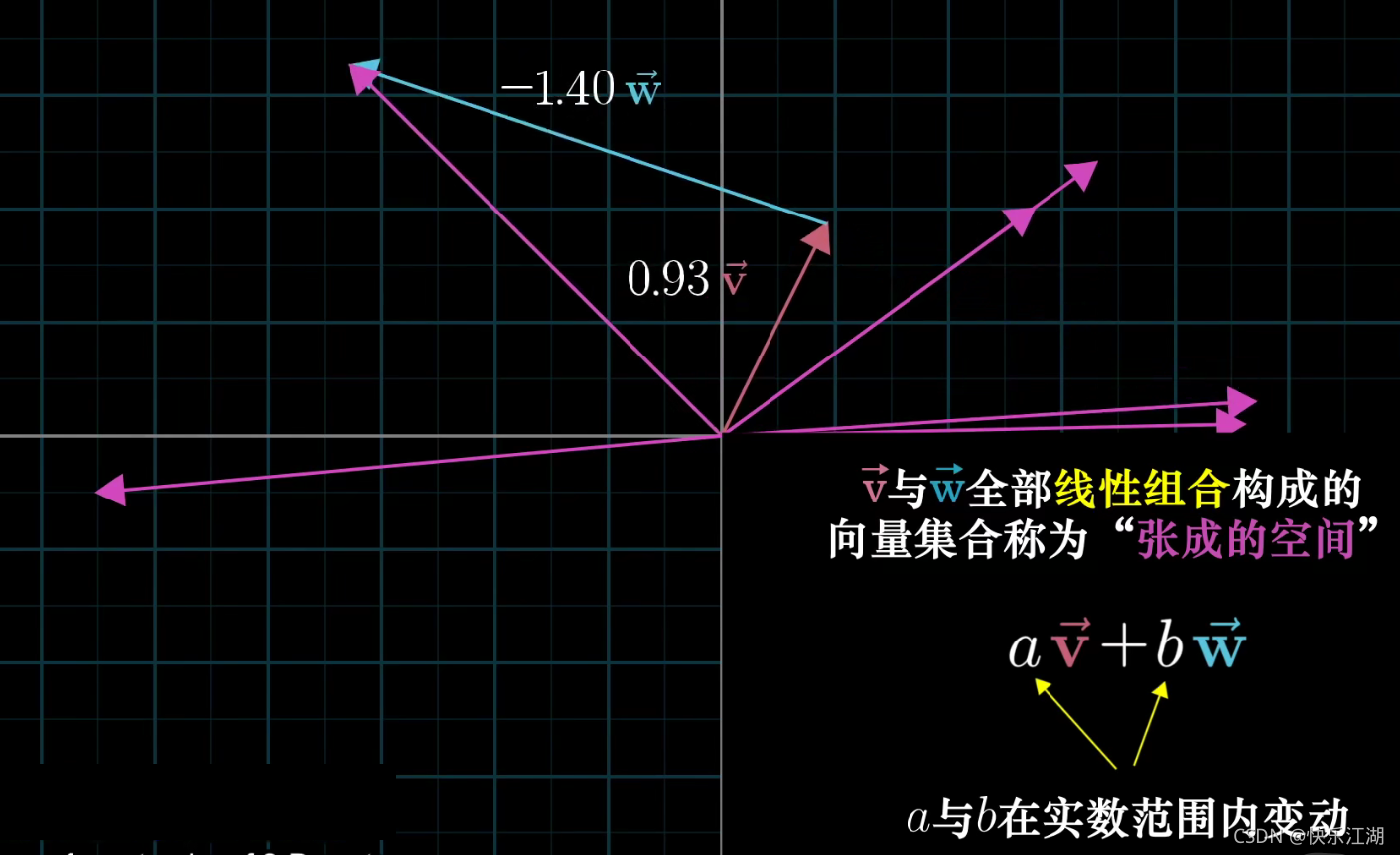
两个向量张成的空间提出了一个问题:仅通过向量加法和向量数乘这两种基础的运算,能获得的所有向量的集合是什么?
所以在三维空间中,取两个不同指向的向量,其张成的空间就是过某个原点的平面

如果让第三个向量落在前面两个向量张成的空间中,那么它们张成的空间将不会发生变化,或者通俗点说,这个向量就会被困在这个空间内
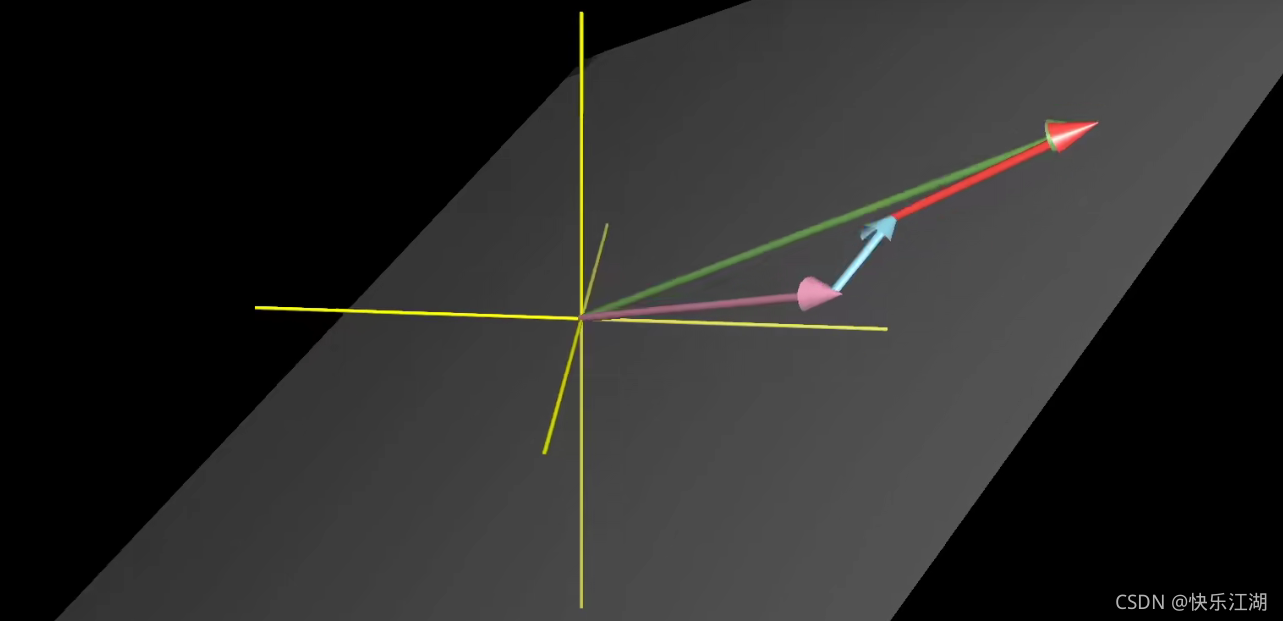
(3)特征向量与特征空间
- 注意:这里的特征向量不是矩阵中的那个特征向量,是用于描述某个事物或某个特征的向量
特征向量:本质就是一个向量,在实际场景中,用于描述一个事务、数据或问题,它有很多维度或者属性。例如:
- 银行会用一个特征向量(包括个人信用度,收入来源、是否有房等分量)来描述贷款人是否具有偿还贷款的能力
特征空间:在特征向量中,由各个维度可能的取值所张成的空间,称之为特征空间。显然,特征空间限定了特征向量的取值范围。所以在特征中,任意一个向量代表的都是 n 维空间中的一个点;反过来, 空间中的任意点也都可以唯一地用一个
向量表示
- 具体见“二”

五:向量线性相关性
(1)数学角度解释
线性无关:任取特征空间中的 n n n个特征向量 x 1 , x 2 , . . , x n x_{1},x_{2},..,x_{n} x1,x2,..,xn,如果当且仅当标量值 a 1 = a 2 = . . . = a n = 0 a_{1}=a_{2}=...=a_{n}=0 a1=a2=...=an=0时,才有 a 1 x 1 + a 2 x 2 + , . . . , + a n x n = 0 a_{1}x_{1}+a_{2}x_{2}+,...,+a_{n}x_{n}=0 a1x1+a2x2+,...,+anxn=0成立,就说这 n n n个特征向量是线性无关的,也就是说,其中任意一个向量不能写成由其他向量的数乘与加法运算构成的线性组合
(2)空间角度解释
根据前面所述,在一组向量中,有个别向量是“多余的”,去掉它们,向量张成的空间不会减少,那么我们就称它们是线性相关的

反之,如果所有向量都给张成的空间增添了新的维度,那么我们就称它们是线性无关的

因此,向量空间的一组基是张成该空间的一个线性无关向量集合







![[附源码]计算机毕业设计JAVA企业信息网站](https://img-blog.csdnimg.cn/c1c64873b1bb422fb3ebea351d6dc0d8.png)