1. 变形梯度

a. 运动变形前，参考构型中某代表性物质点 A 邻域内的线元：
$$d\vec{X}=d{X}^A{\vec{G}}_A=d{x}^i{\vec{c}}_i$$
b. 运动变形后，线元 $d\vec{X}$ 映射为当前构型中的线元 $d\vec{x}$：
$$d\vec{x}=d{x}^i{\vec{g}}_i=d{X}^A{\vec{C}}_A$$
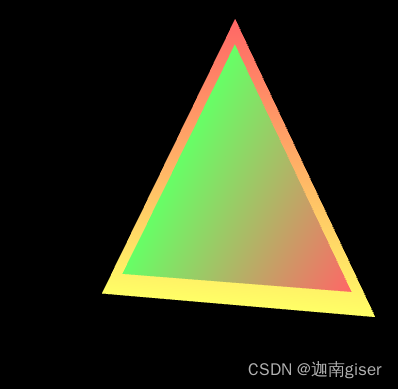
如下图所示：

根据映射关系：
$$\vec{x}=\vec{x}(X^1,X^2,X^3,t)$$
有：
$$d\vec{x}=\frac{\partial \vec{x}}{\partial X^A}d{X}^A=\left(\frac{\partial \vec{x}}{\partial X^A}\otimes {\vec{G}}^A\right)\cdot d\vec{X}\triangleq \mathbf{F}\cdot d\vec{X}$$
将 $\mathbf{F}$ 称作 变形梯度 。可见，变形梯度（仿射量）实现了A点邻域内变形前线元到变形后线元的线性映射。

根据变形梯度的定义与不同坐标系间基的关系，有
$$\begin{array}{rl}& \mathbf{F}\triangleq \frac{\partial \vec{x}}{\partial X^A}\otimes {\vec{G}}^A\triangleq \vec{x}{▽}_0\\ & \\ & ={\vec{C}}_A\otimes {\vec{G}}^A\\ & \\ & =F_{\bullet A}^B{\vec{G}}_B\otimes {\vec{G}}^A\\ & \\ & =x_{,A}^i{\vec{g}}_i\otimes {\vec{G}}^A={\vec{g}}_i\otimes \vec{c}{}^i\\ & \\ & =F_{\bullet i}^j{\vec{c}}_j\otimes \vec{c}{}^i\end{array}$$
由上面的关系可知：

• 变形梯度可写作随体坐标系与固定坐标系基矢的张量积；
• 变形梯度在物质坐标系下的混合分量 $F_{\bullet A}^B$ 也即为物质坐标系与随体坐标系 { X A , t } \{X^A,t\} {XA,t} 间的坐标转换系数 $F_{\bullet A}^B$；
• 变形梯度在空间坐标系下的混合分量 $F_{\bullet i}^j$ 也即为空间坐标系与随体坐标系 { x i , t 0 } \{x^i,t_0\} {xi,t0​} 间的坐标转换系数 $F_{\bullet i}^j$。

另外，变形梯度张量也可由位移在物质坐标系下的右梯度进行表示，由于：
$$\vec{X}+\vec{u}=\vec{x}+\vec{b}$$
式中， $\vec{b}$ 为参考坐标系与空间坐标系原点的位矢差，是常矢。则
$$\mathbf{F}=\frac{\partial \vec{x}}{\partial X^A}\otimes {\vec{G}}^A=\frac{\partial }{\partial X^A}(\vec{X}+\vec{u})\otimes {\vec{G}}^A=\mathbf{I}+\frac{\partial \vec{u}}{\partial X^A}\otimes {\vec{G}}^A=\mathbf{I}+\vec{u}{▽}_0$$

变形梯度的行列式：
$$\begin{gathered} \mathcal{J}\triangleq det(\mathbf{F})=det([F_{\bullet A}^B])=det([g_i^B][x_{,A}^i])=det([x_{,A}^i])\left|\begin{array}{ccc}{\vec{G}}^1\cdot {\vec{g}}_1& {\vec{G}}^1\cdot {\vec{g}}_2& {\vec{G}}^1\cdot {\vec{g}}_3\\ & & \\ {\vec{G}}^2\cdot {\vec{g}}_1& {\vec{G}}^2\cdot {\vec{g}}_2& {\vec{G}}^2\cdot {\vec{g}}_3\\ & & \\ {\vec{G}}^3\cdot {\vec{g}}_1& {\vec{G}}^3\cdot {\vec{g}}_2& {\vec{G}}^3\cdot {\vec{g}}_3\end{array}\right| \\ =det([x_{,A}^i])[{\vec{G}}^1\cdot ({\vec{G}}^2\times {\vec{G}}^3)][{\vec{g}}_1\cdot ({\vec{g}}_2\times {\vec{g}}_3)]=det([x_{,A}^i])\sqrt{\frac{g}{G}}\ne 0 \end{gathered}$$
其中，
$$G={\vec{G}}^1\cdot ({\vec{G}}^2\times {\vec{G}}^3)；g={\vec{g}}_1\cdot ({\vec{g}}_2\times {\vec{g}}_3)$$
或者
$$C=det([C_{AB}])=det([F_{\bullet A}^M{]}^T[G_{MN}][F_{\bullet B}^N])=de{t}^2(\mathbf{F})G$$
则
$$de{t}^2(\mathbf{F})=\frac{C}{G}\ne 0$$
变形梯度的行列式不为零，说明变形梯度是正则仿射量。

2. 变形梯度的逆

根据映射关系：
$$\vec{X}=\vec{X}(x^1,x^2,x^3,t)$$
得：
$$d\vec{X}=\frac{\partial \vec{X}}{\partial x^i}d{x}^i=\left(\frac{\partial \vec{X}}{\partial x^i}\otimes \vec{g}{}^i\right)\cdot d\vec{x}\triangleq \stackrel{-1}{\mathbf{F}}\cdot d\vec{x}$$
根据定义：
$$\begin{array}{rl}& \stackrel{-1}{\mathbf{F}}\triangleq \frac{\partial \vec{X}}{\partial x^i}\otimes \vec{g}{}^i\triangleq \vec{X}▽\\ & \\ & ={\vec{c}}_i\otimes {\vec{g}}^i\\ & \\ & =\stackrel{-1}{F}{}_{,i}^j{\vec{g}}_j\otimes {\vec{g}}^i\\ & \\ & =X_{,i}^A{\vec{G}}_A\otimes {\vec{g}}^i={\vec{G}}_A\otimes {\vec{C}}^A\\ & \\ & =\stackrel{-1}{F}{}_{,A}^B{\vec{C}}_B\otimes {\vec{C}}^A\\ & \\ & =\frac{\partial }{\partial x^i}(\vec{x}-\vec{u})\otimes {\vec{g}}^i\\ & \\ & =\mathbf{I}-\frac{\partial \vec{u}}{\partial x^i}\otimes {\vec{g}}^i=\mathbf{I}-\vec{u}▽\end{array}$$
又因为：
$$\stackrel{-1}{\mathbf{F}}\cdot \mathbf{F}=({\vec{c}}_i\otimes {\vec{g}}^i)\cdot ({\vec{g}}_j\otimes \vec{c}{}^j)={\delta }_j^i{\vec{c}}_i\otimes \vec{c}{}^j=\mathbf{I}$$
因此，$\stackrel{-1}{\mathbf{F}}$ 为变形梯度仿射量的逆。

3. 相对变形梯度

4. 两点张量

定义：若某张量的分量或张量基涉及两个不互相独立的坐标系，便称之为 两点张量。

比如，变形梯度或其逆为两点张量的实例:
$$\mathbf{F}=F_{\bullet A}^B{\vec{G}}_B\otimes {\vec{G}}^A$$
上述形式上似乎只与物质坐标系相关，但注意到：
$$F_{\bullet A}^B=X_{,i}^A{g}_B^i=\frac{\partial X^A(\vec{x},t)}{\partial x^i}\frac{\partial x^i(\vec{X},t)}{\partial X^B}$$
说明其分量涉及物质坐标系与空间坐标系。

最后尤其指出：两点张量关于坐标的导数应当是全导数。具体来说，若张量 $\mathbf{\Psi }$ 是建立在坐标系 { X ⃗ } \{\vec{X}\} {X } 与 { x ⃗ } \{\vec{x}\} {x } 上的两点张量，则
$$\frac{d\mathbf{\Psi }}{d{X}^A}=\frac{\partial \mathbf{\Psi }}{\partial X^A}+\frac{\partial \mathbf{\Psi }}{\partial x^i}\frac{\partial x^i}{\partial X^A}$$