递归
程序调用自身的编程技巧称为递归。
在调用函数时系统需要完成3件事:
- 将所有实参(指针),返回地址传递给被调用的函数
- 为被调用函数的局部变量分配存储区
- 将控制转移到被调用函数的入口
从被调用函数返回时系统也要做3件事:
- 保存被调用算法的计算结果(返回值)
- 释放分配给被调用算法的存储空间
- 依照被调算法保存的返回地址将控制转移回到调用算法
递归过程执行时需多次调用自身。多个(相同)函数嵌套调用,信息传递和控制转移通过栈实现
- 每一次递归调用时,需要为过程中所使用的参数、局部变量等另外分配存储空间
- 层层向下递归,退出时次序正好相反
- 每层递归调用需分配的空间形成递归工作记录,用栈按照后进先出规则管理这些信息
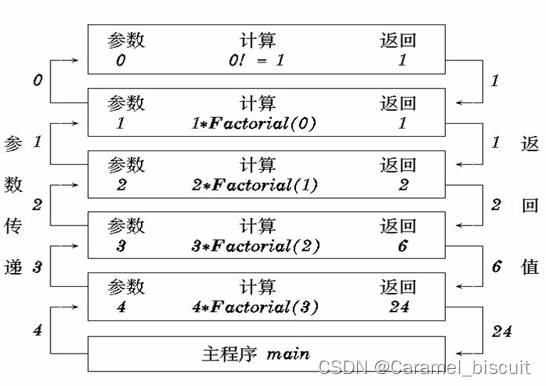
如果函数调用它本身,那么此函数就是递归的,例如求n!
int factoria(int n){
if(n<=1){
return 1;
}else{
return n*factoria(n-1);
}
}
遇到如下三种情况,可以考虑使用递归
- 问题定义是递归的
- 解决问题时采用的数据结构是递归定义的
- 问题的求解过程是递归的
问题定义是递归的
递归法求幂
int power(int x, int n)
{
if ( n == 0 )
return 1;
else
return x * power(x,n-1);
}
可简化为:
int power(int x,int n){
return 0 ? 1 : x*power(x,n-1)
}
斐波那契数列(黄金分割数列):假设一对初生兔子一个月才到成熟期,而一对成熟兔子每月会生一对兔子,那么由一对初生的兔子开始,n个月后会有几对兔子?1、1、2、3、5、8、13、21、…这个数列从第三项开始,每一项都等于前面两项之和。

递归求解斐波那契数列,重复求解子问题,算法复杂度O(2n)
long fib1(int n){
if(n <= 1){
return 1;
}
else{
return fib(n-1)+fib(n-2);
}
}
递推求解斐波那契数列数列,而F(n) = F(n-1) + F(n-2); (n>=2),F(n)具有无后效性,只需记住前两个状态的结果即可,算法复杂度O(n)。
long fib2(int n){
long f1 = 1,f2 = 1,fu;
for(int i=2; i<=n;i++){
fu = f1 + f2;
f1 = f2;
f2 = fu;
}
return fu;
}
问题采用的数据结构是递归的
二叉树链式存储结构:二叉链表。
typedef struct node{
Entrytype data;
struct node *lchild,*rchild;
}BTNode,*BTPtr;
在n个结点的二叉链表中,共有2n个指针,所有有n-1个指针指向结点,所有有n+1个空指针域。
中序遍历递归算法
void inOrder(BTPtr bt){
if(bt != NULL){
inorder(bt->lchild);
printf("%c\t",bt->data);
inorder(bt->rchild);
}
return;;
}
后序遍历
void postOrder(BTPtr bt){
if(bt != NULL){
postOrder(bt->lchild);
postOrder(bt->rchild);
printf("%c\t",bt->data);
}
return;
}
问题的求解过程是递归的
汉诺塔问题:有A、B、C3个塔座,在塔座A上有一叠共n个圆盘,自上而下由小到大叠在一起,编号为1,2,…,n,:要求将塔座A上的圆盘全部移到塔座C上,仍按同样顺序叠置。在移动圆盘时遵守以下规则:每次只允许移动1个圆盘,任何时刻都不允许将较大的圆盘压在较小的圆盘之上
将3个盘子从A移到C,以B为辅助,共7步(2n-1次)完成。
用递归技术求解汉诺塔问题:
- 当n=1时,问题可以直接求解,一步完成。
- 当n>1时,分三步完成:将n-1个较小盘子设法移动到辅助塔座(构造出一个比原问题规模小1的问题),将最大的盘子从原塔座移至到目标塔座,将n-1个较小的盘子设法从辅助塔座移至到目标塔座。
void hanoi(int n,int src,int tar,int aux){
if(n > 0){
hanoi(n-1,src,aux,tar);//将n-1个盘子从原塔座移到辅助塔座上。
move(src,tar);//将源塔座上最后的1个盘子移到目标塔座上。
hanoi(n-1,aux,tar,src);//将辅助塔座上n-1个盘子移到目标塔座上。
}
}
排列问题:生成n个元素的全排列
void swap(int &a,int &b){
int temp = a;
a = b;
b = temp;
}
void Perm(int list[],int k,int m){
//当只剩下一个元素时
if(k == m){
for(int i=1;i<=m;i++){
printf("%d\t",list[i]);
}
}else{
for(int i=k;i<=m;i++){
swap(list[k],list[i]);
Perm(list,k+1,m);
swap(list[k],list[i]);
}
}
}
整数划分问题:将正整数n表示成一系列正整数之和:n=n1+n2+…+nk,其中n1>=n2>=…nk
q(n,m):最大加数n1不大于m的划分个数记作q(n,m),
- q(n,n) = 1+q(n,n-1):正整数n的划分由n1=n和n1<=n-1的划分组成。
- q(n,m) = q(n,m-1) + q(n-m,m)
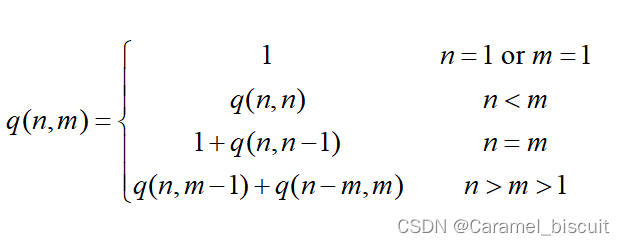
int q(int n,int m){
if(n < 1 || m < 1){
return 0;
}else if(n == 1 || m == 1){
return 1;
}else if(n == m){
return q(n,n-1) + 1;
}else{
return q(n,m-1) + q(n-m,m);
}
}
递归算法:直接或间接地调用自身的算法。
递归函数:用函数自身给出定义的函数。
边界条件和递归方程是递归的两个基本要素。
递归小结
递归算法的优点:结构清晰,易于理解,而且容易用数学归纳法来证明算法的正确性,因此用递归技术来设计算法很方便。
递归算法的缺点:在执行时要多次调用自身,运行效率低,无论是计算时间还是占用存储空间都要比非递归算法要多。一些运算步骤可能重复运行,会进一步降低效率。