基于时间序列的预测,一定要明白它的原理,不是工作原理,而是工程落地原因。
基于时间序列,以已知回归未知----这两句话是分量很重的。
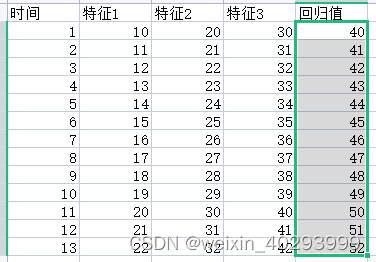
多因素单步单输出组合
时间序列:t=1 是 特征 1,2,3 预测t=2 的回归值41
多因素单步多输出组合
时间序列:t=1 是 特征 1,2,3 预测t=2 的回归值1 41 回归值2 xxxx
所以在看lstm git项目的时候,通常会有一个充足数据集的过程:
叫做 构造多元监督学习型数据
# 构造多元监督学习型数据
def split_sequences(sequences, n_steps):
X, y = list(), list()
for i in range(len(sequences)):
# 获取待预测数据的位置
end_ix = i + n_steps
# 如果待预测数据超过序列长度,构造完成
if end_ix > len(sequences)-1:
break
# 取前n_steps行数据的前5列作为输入X,第n_step行数据的最后一列作为输出y
seq_x, seq_y = sequences[i:end_ix, :5], sequences[end_ix, 5:]
X.append(seq_x)
y.append(seq_y)
return array(X), array(y)
实际就是完成数据的重新错位分配,
原始数据是
t1 的 feature1, feature2, feature3, feature4 和 y1在一列,
t2 的 feature1, feature2, feature3, feature4 和 y2在一列,
t3 的 feature1, feature2, feature3, feature4 和 y3在一列,
t4 的 feature1, feature2, feature3, feature4 和 y4在一列,
基于
3因素单步单输出组合 但经过这个函数 要改成
t1 的 feature1, feature2, feature3, feature4 和 y2在一列,
t2 的 feature1, feature2, feature3, feature4 和 y3在一列,
t3 的 feature1, feature2, feature3, feature4 和 y4在一列,
3因素2步单输出组合
[
[t1 的 feature1, feature2, feature3, feature4 ]、 [t2 的 feature1, feature2, feature3, feature4] , y3],在一列
[
[t2 的 feature1, feature2, feature3, feature4 ]、 [t3 的 feature1, feature2, feature3, feature4] , y4],在一列
理就是这么个理论,但是写出能实现 m因素n时间步长预测,p时间步长,q特征的回归并不太容易。
代码整理中,后续上传