代码随想录二刷Day24
今日任务
理论基础
77.组合
语言:C++
理论基础
- 解决的问题
① 组合问题:不考虑顺序
② 切割问题
③ 子集问题
④ 排列问题:考虑顺序
⑤ 棋盘问题:N皇后,解数独 - 回溯法三部曲
① 回溯函数模板返回值以及参数
函数名:backtracking
返回值:void
参数:先写逻辑,再确定需要什么参数
② 回溯函数终止条件:搜索到叶子节点
③ 回溯搜索的遍历过程 - for循环是横向遍历,backtracking(递归)是纵向遍历
- 回溯模板
void backtracking(参数){
if(终止条件){
存放结果;
return;
}
for(选择:本层集合中的元素(树中节点孩子的数量就是集合的大小)){
处理节点;
backtracking();
回溯,撤销处理结果;
}
}
77. 组合
链接:https://leetcode.cn/problems/combinations/
class Solution {
public:
vector<vector<int>> res;
vector<int> combination;
//curLen没有必要,直接combination.size()即可
void backtracking(int n, int k, int cur, int curLen){
if(curLen == k){
res.push_back(combination);
return;
}
for(int i = cur; i <= n; i++){
combination.push_back(i);
backtracking(n, k, i + 1, curLen + 1);
combination.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1, 0);
return res;
}
};
剪枝优化
class Solution {
public:
vector<vector<int>> res;
vector<int> combination;
void backtracking(int n, int k, int cur){
if(combination.size() == k){
res.push_back(combination);
return;
}
//循环终止条件优化
for(int i = cur; i <= n - (k - combination.size()) + 1; i++){
combination.push_back(i);
backtracking(n, k, i + 1);
combination.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(n, k, 1);
return res;
}
};
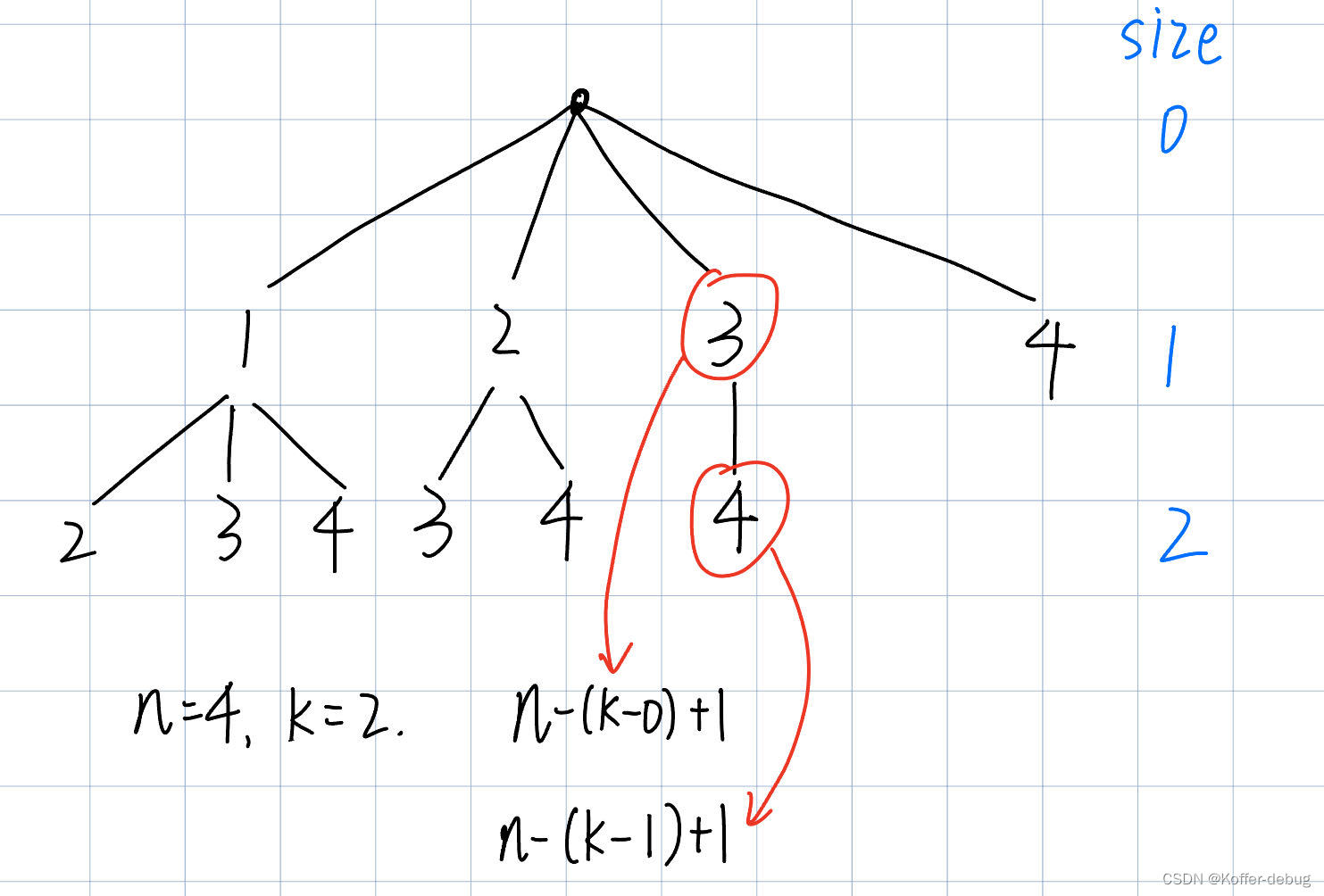
可以看到剪枝优化后效率有了很大提升