1 线段树上的操作

• push_up(int u)：由子节点的信息去计算父节点的信息，例如两个子节点的区间和，加起来就是父节点表示的区间和。其中u是当前节点编号，表示用u的左右两个子节点来算一下自己这个节点的信息。
• push_down：将父节点的信息下传到子节点，例如将整个区间加上同一个数，那么将这个操作递归地下传给子节点。push_down也叫做懒标记或者延迟标记。
• build(int u, int L, int R)：将一段区间初始化成线段树。其中u是当前节点编号，L是区间左端点， R是区间右端点。
• modify：修改操作，可以分为修改单点（比较简单）和修改一个区间（比较复杂，往往需要应用push_down来延迟更新）。
• query(int u, int L, int R)：查询操作，查询某一段区间的信息。其中u是当前节点编号，L是查询区间左端点， R是查询区间右端点。

2 一个例子

线段树除了最后一层之外，形态上是一个满二叉树。比如要维护[1, 10]这个区间，那么根节点就表示[1, 10]。取mid = (L + R) / 2下取整，那么左子节点表达的区间是[L, mid]，右子节点表达的区间是[mid + 1, R]。所以维护[1, 10]的线段树就是：

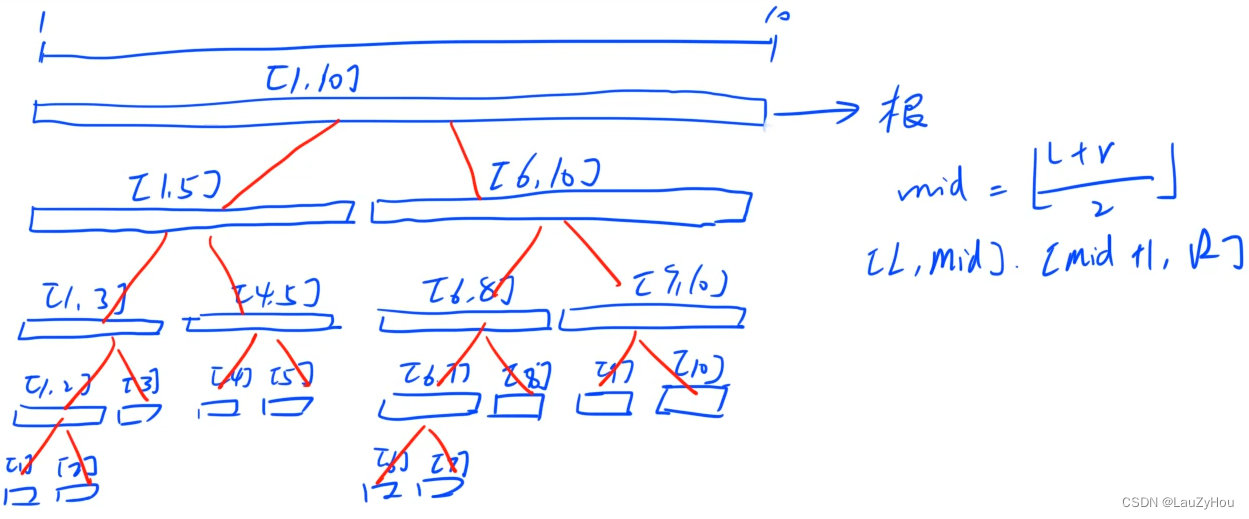
之前学习的堆也是这样除了最后一层之外就是一个满二叉树的形态， 所以我们存储线段树的方式和堆也是类似的，用一个一维数组来存整棵树。所以对于编号是x的节点，父节点是x / 2下取整（即x >> 2），左儿子的编号是2x（即x << 1），右儿子是2x + 1（即x << 1 | 1）。

3 线段树的空间效率

假设区间里一共有n个最小粒度的区间，估计一下线段树上最坏情况下有多少个节点。
首先叶子节点也就是最小粒度的区间，一定是有n个叶子节点。
那么倒数第二层最坏情况下不会超过叶子节点的个数，也就认为倒数第二层最多n个节点。
那么去掉倒数第一层以外的部分是满二叉树，满二叉树的部分最多就是2n - 1个节点（通过刚刚估计的倒数第二层的最坏情况来计算的）。
那么最后一层最坏情况下是倒数第二层的两倍，也就是最后一层最坏情况下2n个节点。
所以整棵树最坏情况下不会超过(2n - 1) + 2n = 4n - 1个节点，所以开线段树的时候直接开4n个节点这么多的空间。

4 build操作

将区间[L, R]构建到线段树里，节点编号为u，伪代码：

build(int u , int L , int R)
{
	// 记录一下区间左右端点
	tr[u].L = L
	tr[u.R = R
	// 如果是叶子节点就build完成了
	if (L == R) return // 叶子节点因为没有孩子，所以是不用push up的
	// 计算一下中点，递归build左右两边
	int mid = L + R >> 1
	build(u << 1, L, mid)
	build(u << 1 | 1, mid + 1, R)
	// 一般是在这里，也就是子树都build完的时候，函数退栈之前push up一下，用两个子节点反向计算当前节点信息
	push_up(u)
}

5 query操作

假设线段树的每个节点维护的是区间的最大值，在[1, 10]的线段树里要查询[5, 9]这个区间，那么会从根节点开始递归地查询。具体地，要查询的区间[L, R] = [5, 9]，当前（在根节点）线段树上节点表示的区间是[TL, TR] = [1, 10]。那么[L, R]和[TL, TR]之间的包含关系决定了query的下一步动作：

1. 待查询的[L, R]完全包含了当前节点的[TL, TR]，这时直接返回[TL, TR]的结果。
2. 待查询的[L, R]和当前节点的[TL, TR]有交集，那么对左右子节点，有交集的就（分别）递归处理。
3. 待查询的[L, R]和当前节点的[TL, TR]没有交集，这种情况是不存在的，只要我们保证有交集的时候才会递归调用对这棵子树的处理就能保障这件事了。

在这个例子中，标上黄色圈圈的部分是被递归query到的节点区间。

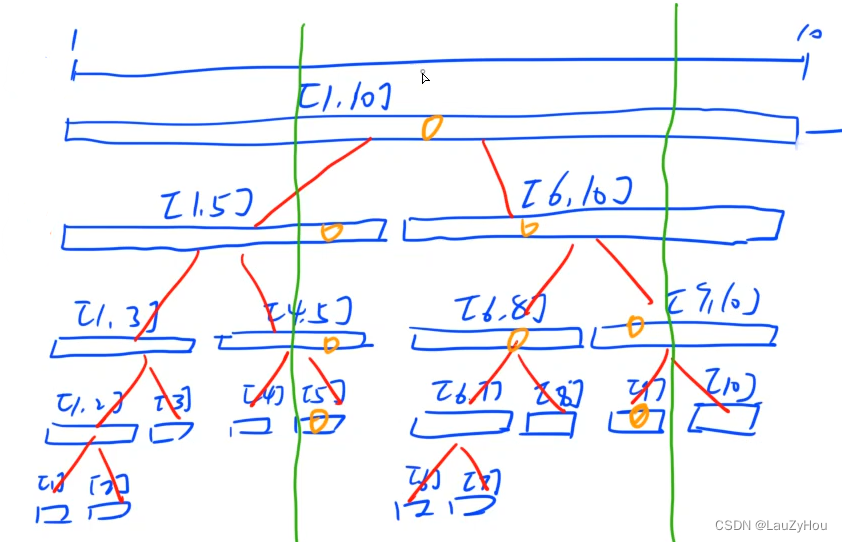
这个例子里因为要查的区间比较小所以比暴力做法要查的区间还多了（暴力是查5个，线段树要查8个），但是可以证明线段树的查询效率是log(n)的常数倍，这段证明先略过不看了。

6 单点modify操作

单点modify最终一定会改到某一个叶子节点上去，所以从上到下只要每次往一个子树里去递归调用modify，直到叶子节点的时候把叶子节点的信息改掉，然后在递归退栈的时候沿着调用链对所有非叶子节点push_up重新计算一下即可。

7 push_up操作

用tr[u << 1]和tr[u << 1 | 1]的信息更新计算tr[u]的信息。

8 例题

8.1 AcWing 1275 最大数

这题只带query和单点modify操作，而且线段树节点除了存查询信息，不需要额外信息。

8.2 AcWing 245 你能回答这些问题吗

这题也是只带query和单点modify操作，但是线段树节点除了存查询信息，还需要额外信息。这个区间信息是最大后缀和和最大前缀和，用来计算父节点横跨两个区间时候的最大子段和。

横跨两个区间的最大字段和=左子区间最大后缀和+右子区间的最大前缀和。

但是新加入的这两个额外信息也需要能从两个子节点的信息算出来，为了处理盖掉一个子区间的最大前缀或者最大后缀和，还需要存一个区间总和的信息：

再考虑这个区间总和的信息，一定能从子节点的总和信息算出来，这样就形成闭环了（用y总的话说是完备的）。

8.3 AcWing 246 区间最大公约数

这题除了query操作之外，还带有区间modify操作，但是不需要懒标记push_down的原因是因为我们可以将这个区间modify操作转换成线段树上的单点modify操作。

具体地，考虑到这题的两个操作是：

1. 区间$[L,R]$增加一个数
2. 查询区间的最大公约数

考虑到区间$[L,R]$增加一个数可以转换成对差分数组的$L$位置增加一个数，再对$R+1$位置减去这个数，可以试着考虑能不能用差分数组扔到线段树里去维护。

因为$a_1,a_2,...,a_n$的最大公约数就等于$a_1,a_2-a_1,...,a_n-a_{n-1}$的最大公约数，所以如果记
$$b_i=a_i-a_{i-1}$$

那么对$a$数组求区间[L, R]的最大公约数，等同于先求
$$b_{L+1},...b_R$$

的最大公约数，再和$a_L$求一下最大公约数即可。那么前者就是差分数组的最大公约数了，直接扔到线段树里维护，线段树结点只放最大公约数这个信息的话，对最大公约数的计算就已经是完备的了，因为可以从两个子节点的最大公约数求一下最大公约数得到父区间的最大公约数。然后在对整个区间增加一个数的时候，其实就是做了两次单点modify。

另外就是怎么求$a_L$的问题，它相当于是我们维护的差分数组到$L$为止的前缀和，因为前缀和也是一个区间和，所以我们直接在线段树里再顺便维护一个区间和的信息就可以了，区间和信息之于自己也是完备的。这样每次查询$[L,R]$的最大公约数的时候，就是在我们维护的整个差分数列的线段树上先query一下$[L+1,R]$的最大公约数，然后query一下$[1,L]$的区间和，再把两个值求一个最大公约数即可。