第一题 leetcode 704.二分查找

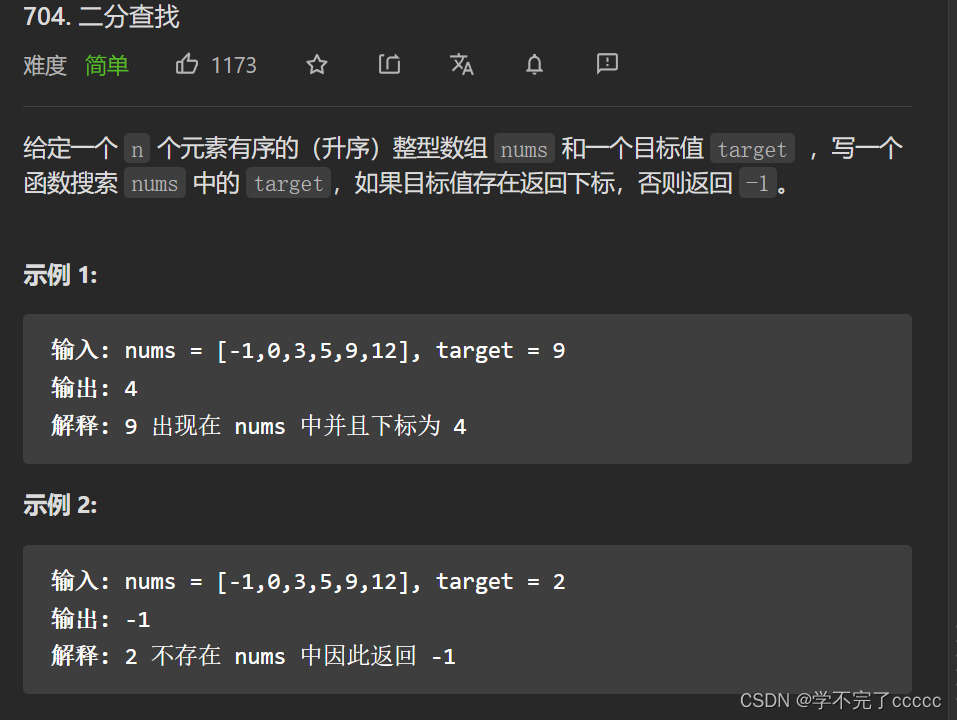
二分法的思路

二分法的思路很简单

• 数组必须有序
• 先查找中间元素进行比较
• 得出大小再考虑向左比较还是向右比较

代码实现

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int middle = 0;
        while(left<=right)
        {
            middle = left + (right - left) /  2;
            if(nums[middle]==target)
            {
                return middle;
            }else if(nums[middle] < target)
            {
                left = middle + 1;
            }else
            {
                right = middle - 1;
            }
        }
        return -1;
    }
};

结果如下

第二题 leetcode 35.搜索插入位置

题目描述

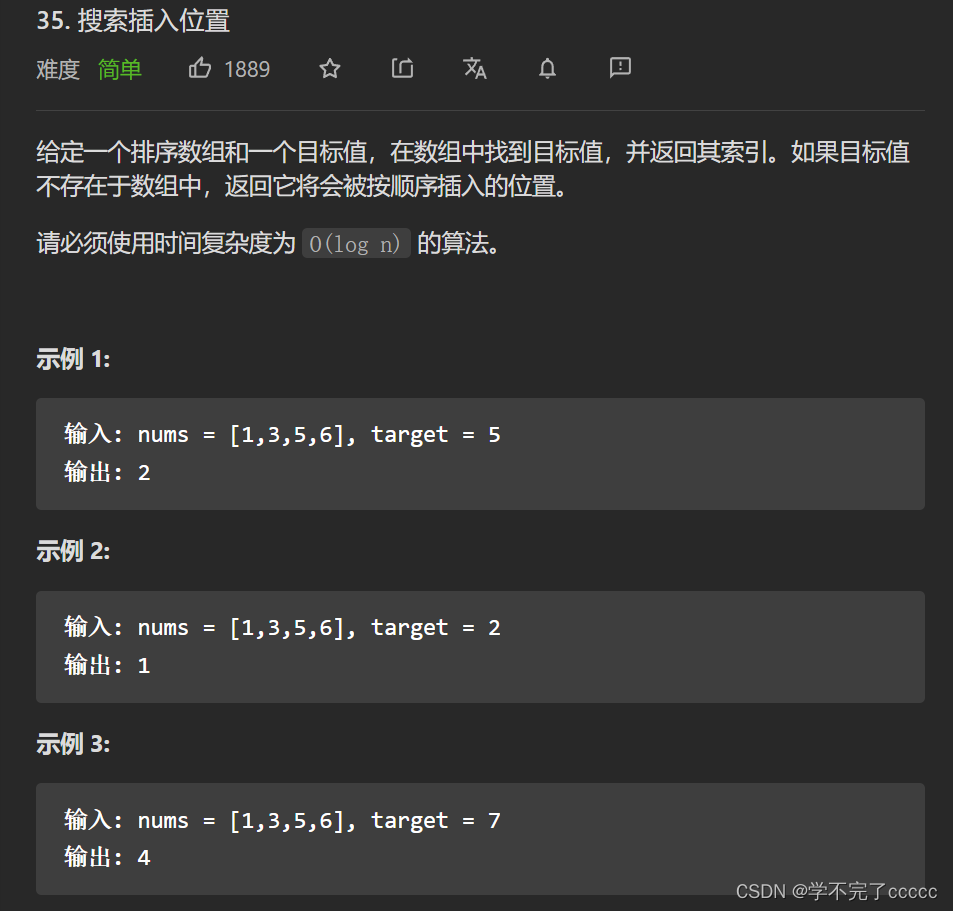
题目分析

和704题的比较如下

• 依旧需要返回可以搜到的下标
• 704搜不到返回-1 本题返回可以插入的位置

代码示例

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        int middle = 0;
        while(left <= right)
        {
            middle = left + (right - left) / 2;
            if(nums[middle]==target)
            {
                return middle;
            }else if(nums[middle] < target)
            {
                left = middle + 1;
            }else
            {
                right = middle - 1;
            }
        }
        // 为何返回left的原因有以下几点
        // 我们需要返回一个正确的有序位置 而且计算到最后返回-1 的时候 已有三个参数 left，middle， right
        return left;
    }
};

明确eft的原因从以下几点来看

• while的限制条件是left大于right的时候，那么一旦找不到righ会-1导致left大于right退出while循环
• 此时left的位置就是要插入的位置

第三题 leetcode 34.

题目描述

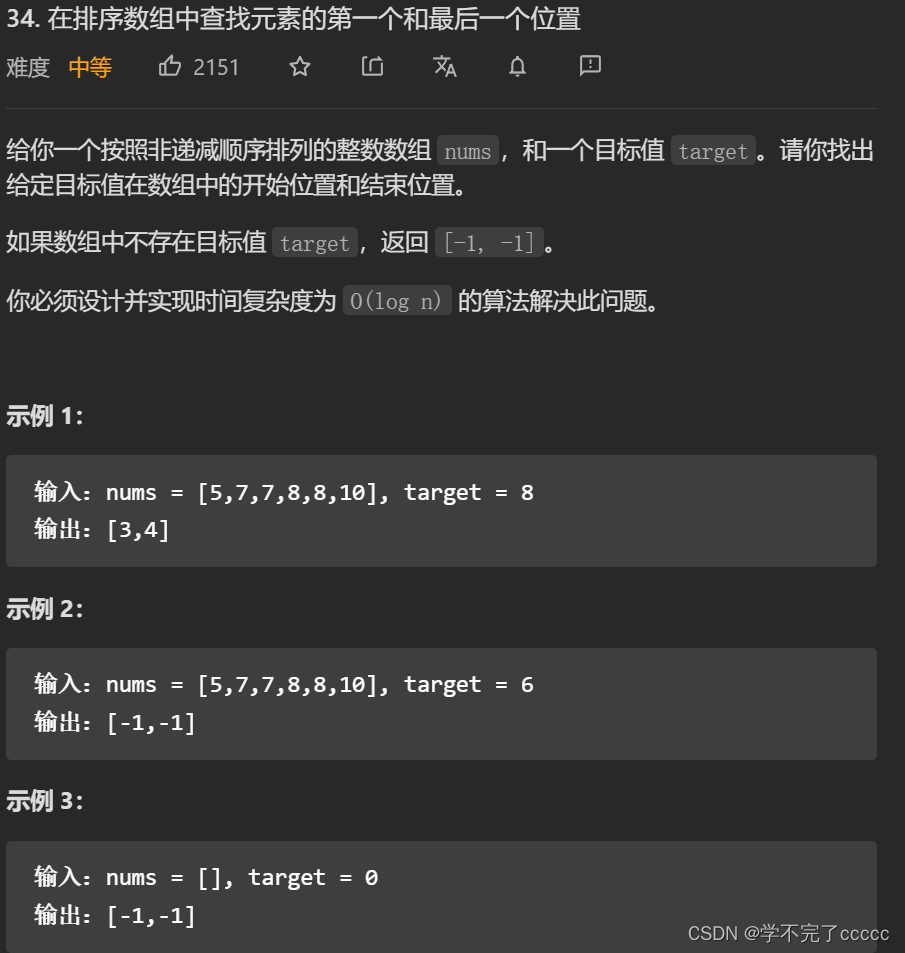
分析

核心就是当边界结束的时候left代表的是什么

代码实现

class Solution {
private:
    int board(vector<int>& nums, int target)
    {
        int left = 0;
        int right = nums.size() - 1;
        int middle = 0;
        while(left<=right)
        {
            middle = left + (right-left) / 2;
            if(nums[middle]<target)
            {
                left = middle + 1;
            }else
            {
                right = middle - 1;
            }
        }
        return left;
        // 返回左边界 即可以查找到的第一个数的位置
    }
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        vector<int> res={-1, -1};
        int start = board(nums, target);
        // 排除三种情况
        if(nums.size()==0 || nums[nums.size()-1] < target || nums[start]!=target)
        {
            return res;
        }
        int end = board(nums, target+1)-1;
        res.clear();
        res.push_back(start);
        res.push_back(end);
        return res;
    }
};

第四题 leetcode 69

题目描述

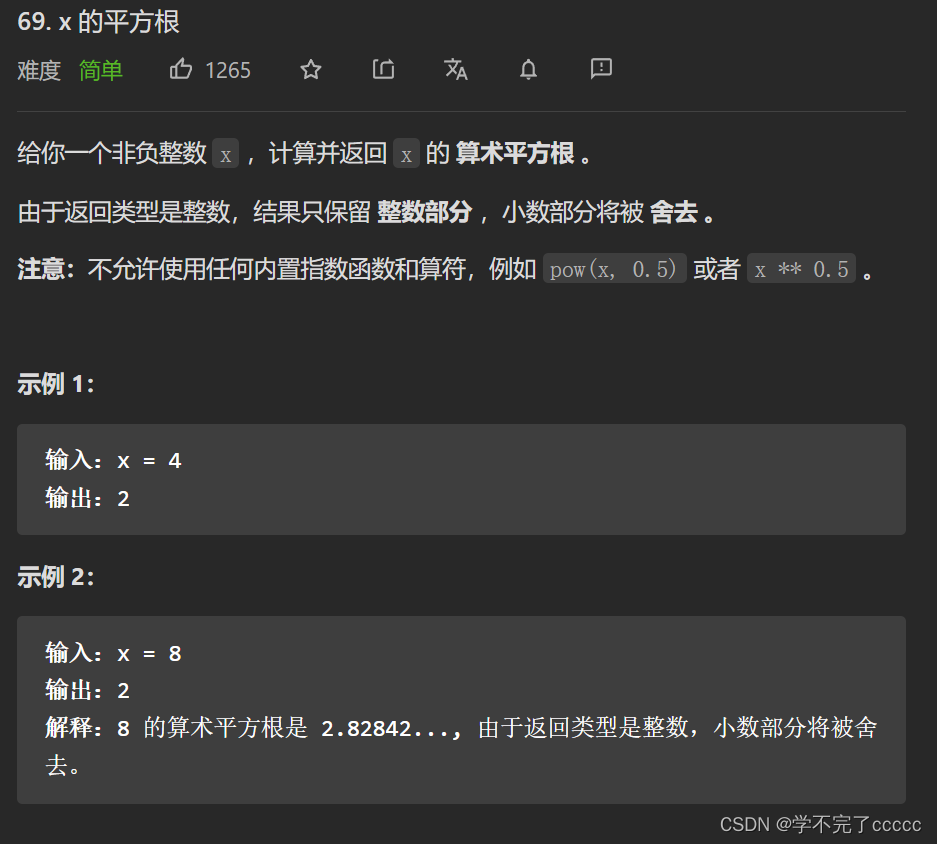
分析

说白了也是搜素 只是现在需要不保留小数的
那么搜素结束之后的right即是较小的那一个，另外将特殊情况排除一下

代码实现

class Solution {
public:
    int mySqrt(int x) {
        int left = 0;
        int right = x;
        int middle = 0;
        if(x==0)
        {
            return 0;
        }
        if(x==1)
        {
            return 1;
        }
        while(left<=right)
        {
            middle = left + (right-left) / 2;
            if(x/middle > middle)
            {
                left = middle + 1;
            }else if(x/middle == middle)
            {
                return middle;
            }else
            {
                right = middle - 1;
            }
        }
        return right;
    }
};

第五题 leetcode 367.

题目描述

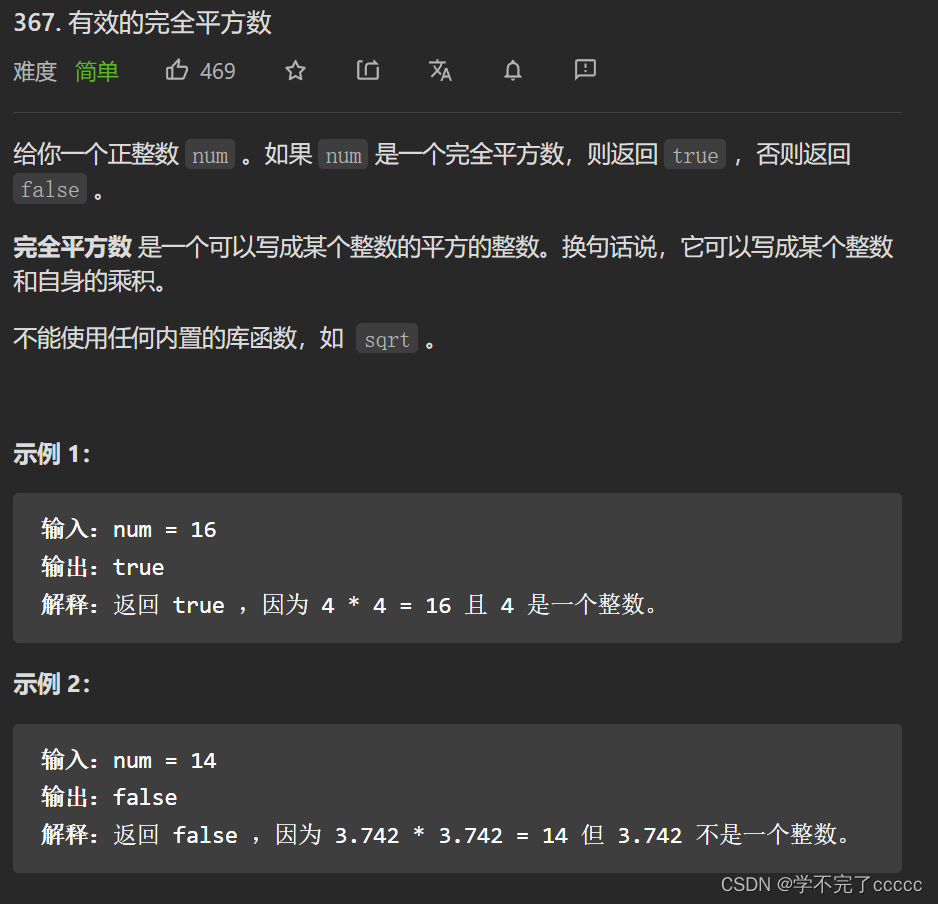
代码实现

class Solution {
public:
    bool isPerfectSquare(int num) {
        int left = 1;
        int right = num;
        int middle = 0;
        if(num==1)
        {
            return true;
        }
        while(left<=right)
        {
            middle = left + (right-left) / 2;
            if(num/middle > middle)
            {
                left = middle + 1;
            }else if((num%middle==0) && (num/middle==middle))
            {	// 来进行判断是否是平方
                return true;
            }else
            {
                right = middle - 1;
            }
        }
        return false;
    }
};